Leetcode NO.74 Search a 2D Matrix & binary search

最新推荐文章于 2025-11-25 00:06:26 发布

原创最新推荐文章于 2025-11-25 00:06:26 发布 · 174 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法

算法同时被 2 个专栏收录

40 篇文章

订阅专栏

leetcode

35 篇文章

订阅专栏

本文探讨了一种针对有序矩阵的高效搜索算法，该算法利用矩阵的特殊排列（每行升序且每行首元素大于前一行尾元素）实现目标值的查找。算法基于二分查找，时间复杂度为O(log(mn))，空间复杂度为O(1)。通过两个测试用例展示了算法的正确性，并提供了具体实现代码。

文章目录

1.问题描述

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

2.测试用例

示例1

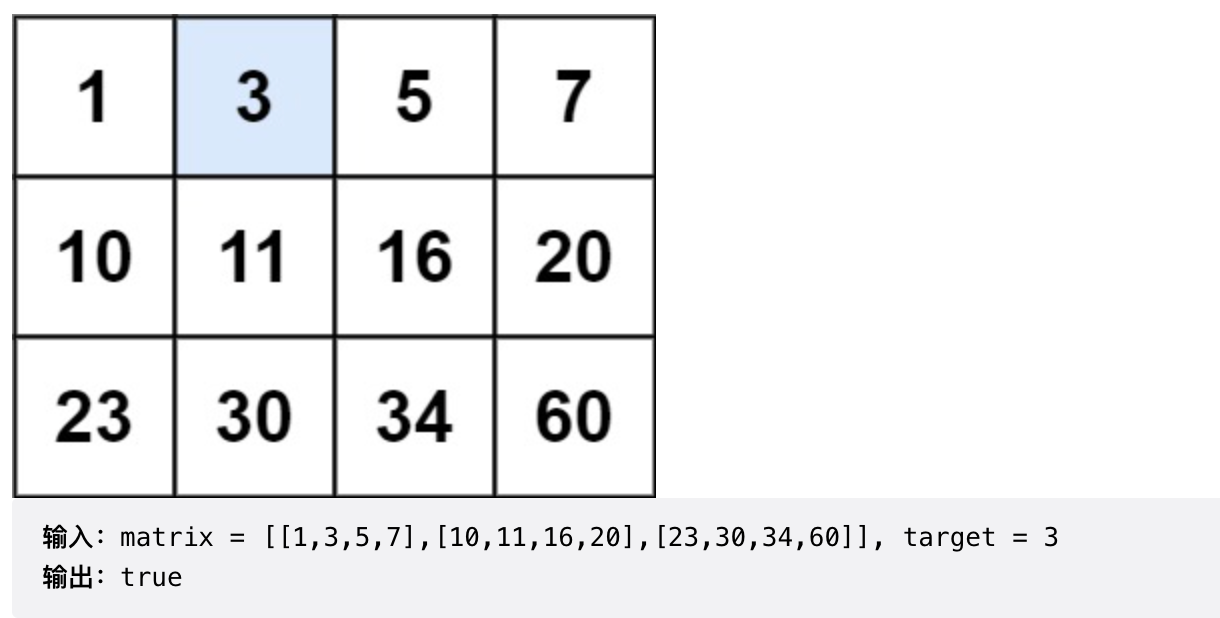
示例2

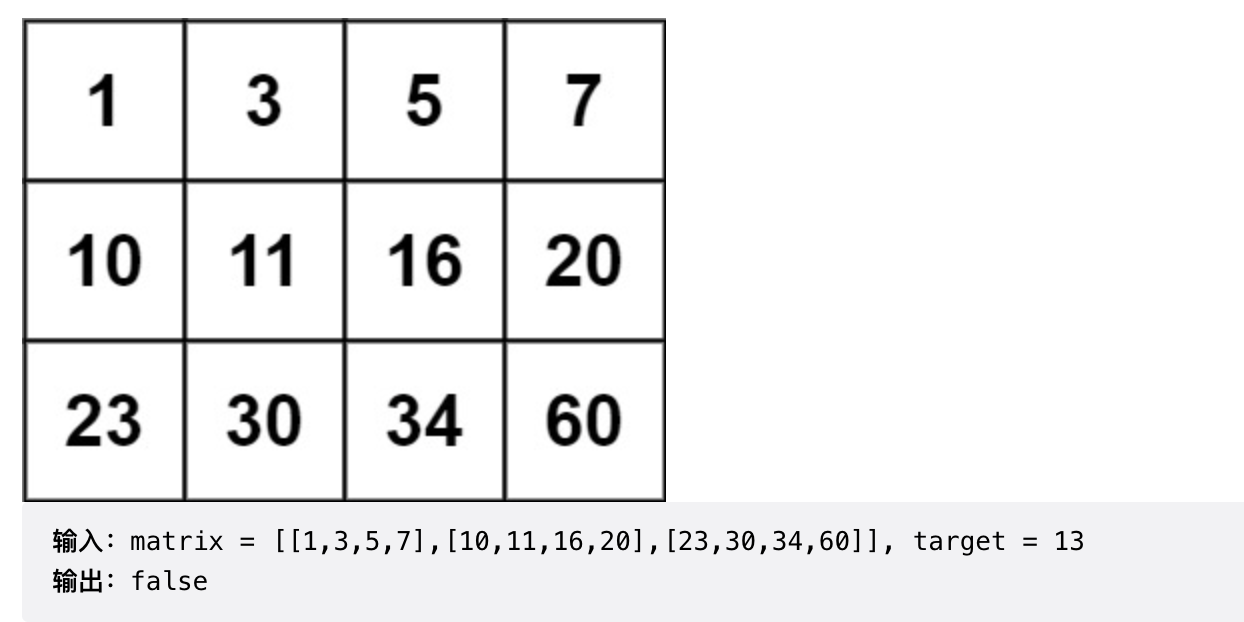
3.提示

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-104 <= matrix[i][j], target <= 104

4.代码

二维矩阵降维成逻辑一维矩阵 & binary search

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length < 1 || matrix[0].length < 1) {
            return false;
        }
        int m = matrix.length;
        int n = matrix[0].length;
        int l = 0;
        int r = m * n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            int midValue = matrix[mid / n][mid % n];
            if (midValue == target) {
                return true;
            } else if (target < midValue) {
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        }
        return false;
    }
}