leetcode64:Minimum Path Sum

最新推荐文章于 2019-08-10 12:43:28 发布

原创最新推荐文章于 2019-08-10 12:43:28 发布 · 371 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #Minimum Path Sum

面试准备同时被 3 个专栏收录

66 篇文章

订阅专栏

JavaSE

54 篇文章

订阅专栏

算法

44 篇文章

订阅专栏

本文详细解析了寻找矩阵中从左上角到右下角的最小路径和的算法实现。通过动态规划方法，构建状态转移方程dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+grid[i][j]，并逐步求解得到最终答案。

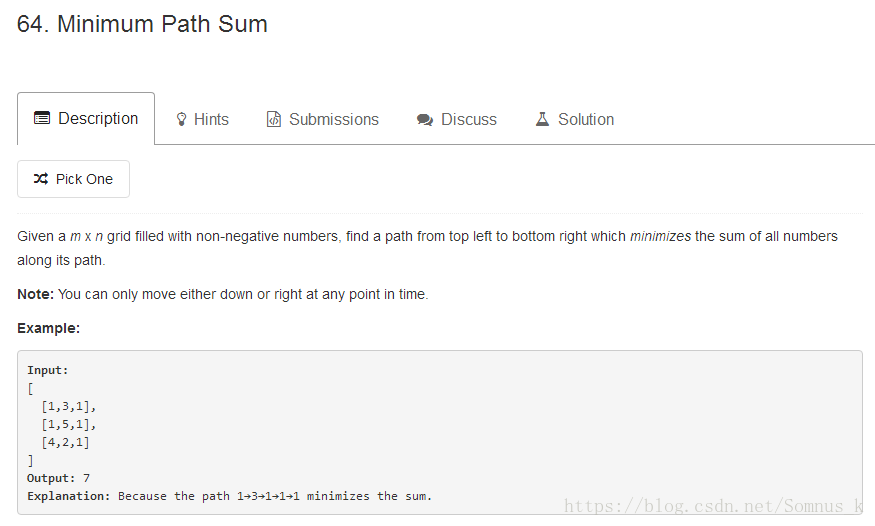
思路：跟之前走方格的题差不多，只是状态转移方程稍微改变一下。dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];。

代码：

public class MinimumPathSum64 {

	public static void main(String[] args) {

//		int[][] num = { { 1, 3, 1 }, { 1, 5, 1 }, { 4, 2, 1 }};
		int[][] num = { { 1, 2,5 }, { 3,2,1 }};
		System.out.println(minPathSum(num));
	}

	public static int minPathSum(int[][] grid) {

		int[][] dp = new int[grid.length][grid[0].length];
		int sum = 0;
		for (int i = 0; i < grid[0].length; i++) {
			sum += grid[0][i];
			dp[0][i] = sum;
		}
		sum = 0;
		for (int i = 0; i < grid.length; i++) {
			sum += grid[i][0];
			dp[i][0] = sum;
		}

		for (int i = 1; i < dp.length; i++) {
			for (int j = 1; j < dp[0].length; j++) {
				dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
			}
		}
		return dp[dp.length - 1][dp[0].length - 1];
	}
}

输出：