寻找凸包问题 （Graham Scan 算法 极坐标序C++实现）

寻找凸包问题 （Graham Scan 算法 极坐标序C++实现）

给定平面上n个点的集合Q，求Q的凸包

• Q的凸包是一个凸多边形P，Q的点或者在P上或者在P内
• 凸多边形P是具有如下性质多边形：连接P内任意两点的边都在P内

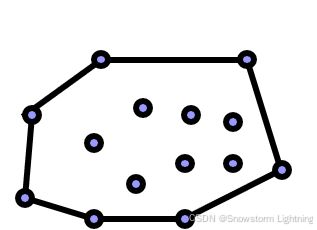
Graham-scan的基本思想

• 找到最下最左顶点，其他顶点与它连线
• 按夹角从小到大排序
• 夹角最小的开始，寻找凸包点

Description

给定平面上N个点, 请找出这N个点的凸包.

Input

第一行输入M表示包含M组测试数据，每组先输入N (N<=100), 接着输入N个坐标(x,y), x和y均为int型整数.

Output

以最下最左点开始逆时针输出凸包, 若有多个点在同一坐标,只输出一个,若凸包上有多个点在同一线上,只输出两端点.

Sample Input

2
7 1 1 4 1 4 4 4 4 1 4 2 2 5 5
8 5 6 8 3 1 8 5 7 3 5 3 5 1 8 2 11

Sample Output

case 1:
1 1
4 1
5 5
1 4
case 2:
8 3
2 11
1 8
3 5

C++代码

#include <iostream>
#include<vector>
#include<algorithm>
#include<cmath>

using namespace std;

struct Point { // 定义 点 Point(x,y)
	double x;
	double y;
	double angle; //向量角度
	double length; // 向量模长

	Point operator-(Point& p) {
		Point t;
		t.x = x - p.x;
		t.y = y - p.y;
		return t;
	}
	bool operator==(Point& p) {
		return x == p.x && y == p.y;
	}
};

int convex[1005]; // 保存组成凸包的点的下标
Point points[1005];

bool compareYX(Point a, Point b) { // 按照优先Y轴，其次X轴，对点进行从小到大的排序，
	if (a.y != b.y)return a.y < b.y;
	return a.x < b.x;
}

bool compareAngle(Point a, Point b) { //优先比较角度，角度相同则比较模长
	if (a.angle != b.angle)return a.angle < b.angle;
	return a.length < b.length;
}
double distance(Point a, Point b) { // 返回两点间距离（向量模长）
	return sqrt(pow((a.x - b.x), 2) + pow(a.y - b.y, 2));
}
double crossProduct(Point a, Point b) { // 返回两向量的叉积
	return a.x * b.y - b.x * a.y;
}

int removeSame(Point points[],int n) {
	int k = 0;
	for (int i = 1; i < n; ++i) {
		if (points[i] == points[k]) continue;
		else {
			++k;
			points[k].x = points[i].x;
			points[k].y = points[i].y;
		}
	}
	return k + 1;
}

void getConvecHull() {
	int n, x, y;
	cin >> n;

	for (int i = 0; i < n; ++i) {
		cin >> points[i].x >> points[i].y;
	}

	sort(points, points + n, compareYX); // 对点进行先Y轴后X轴的从小到大的排序，points[0]为坐标轴上最下边的点中最左边的点

	n = removeSame(points,n); //去除重复点
	
	for (int i = 1; i < n; ++i) {
		points[i].length = distance(points[0], points[i]);
		points[i].angle = acos((points[i].x - points[0].x) / points[i].length); // 通过arccos计算角度
	}
	sort(points + 1, points + n, compareAngle);// 通过角度进行排序

	int total = 0;
	convex[total++] = 0;// 初始点入栈

	for (int i = 1 ; i < n; ++i) {
		while (total > 1 
			&& crossProduct(points[convex[total-1]] - points[convex[total - 2]], points[i] - points[convex[total-1]]) <= 0) {
			// 若 <栈顶的2个点组成的向量> 和 <栈顶的点和当前的点组成的向量> 不满足凸性（即叉积小于等于0），则栈顶元素出栈
			--total;
		}
		convex[total++] = i;
	}

	for (int i = 0; i < total; ++i) {
		cout << points[convex[i]].x << ' ' << points[convex[i]].y << endl;
	}
}

int main() {
	int m;
	cin >> m;
	for (int i = 1; i <= m; ++i) {
		cout << "case " << i << ':' << endl;
		getConvecHull();
	}
}

参考
【计算几何02】凸包问题（Convex Hull）