算法导论期末复习（斐波那契堆）

斐波那契堆

1、斐波那契堆结构

斐波那契堆是由一组最小有序树构成的—无序二项树
其中有序对应的是，父母节点都比孩子节点小。无序是兄弟结点之间并没有先后顺序之分。

与二项堆类似每个斐波那契堆中的结点 $x$ 都有以下结构：

1.父节点指针p[x]。如果结点为堆中无序树的根节点则p[x]=nil。

2.指向任意一个孩子结点的指针child[x]。

3.左右兄弟结点left[x]，right[x]。如果没有左右兄弟，则left[x]=right[x]=nil。并且最右边孩子结点的right[x]=树中第一个节点。

4.记录孩子结点个数的域degree[x]

5.标记结点mark[x]。如果该节点成为另一个节点的孩子结点后，失去了结点，则该节点标记为true。

6.min[H]，指向斐波那契堆 H 中的最小值所在结点的指针。

具体实例可看下图：

此外还需要了解表示斐波那契堆属性的符号：

1. t(H) 根表中树的个数（根表存储堆中无序树的根节点）。

2. n(H) 堆中结点的个数

3. m(H) 表示堆中被标记结点的个数

4. D(n)表示根表中根结点结点的最大度数的上界 （斐波那契堆中D(n)=$lgn$）

由上面所描述，我们定义斐波那契堆的势函数为：

$f(H)=t(H)+m(H)$

当H=0时，该势函数显然成立。

2、斐波那契堆的操作

1）可合并堆的操作

①.、创建斐波那契堆

创建一个空的斐波那契堆。所有参数都为空。

②、插入节点

如果该节点已被分配，直接将该节点插入根表中。比较和min(H)的大小，确定min(H)的值。
操作的平摊代价分析：O(1)

③、寻找最小结点

min(H)

④、合并两个斐波那契堆

简单的将两个斐波那契堆的根表合并。由势函数的定义可知道，堆势

⑤、抽取最小节点

过程描述：
由于是最小结点一定在树的根节点，所以将最小结点的孩子结点都加入到根节点，抽取最小结点 x 。将min(H)=right(x) , 然后不断合并堆中度数相同的结点。直到根表中根节点度数没有相同的为止。

具体伪代码如下图：

其中CONSOLIDATE(H)的伪代码如下图所示：

其中CONSOLIDATE代码中用到了辅助数组A[D(n)]，意味着如果节点 y 的度数为 i ，那么A[i] = y。
代码中第11、12行表示合并以后堆中度数为d的根结点暂时为空。并且由于根节点y成为了x的子节点，所以x结点的度数要加1。

代价分析：
由于堆中最大度数的上界为D[n]，所以在该操作中，最多进行D[n]次将最小值根节点x的孩子结点插入到根表中的操作。所以调用CONSOLIDATE的操作时，根表中结点的个数为D(n)+t(H)-1。意味着CONSOLIDATE中for循环的大小最多为D(n)+t(H)-1，又因为for循环下的while与for循环的次数成正比，所以CONSOLIDATE的工作量最大为O(D(n)+t(H))，又因为合并后堆中最多有D(n)+1个结点的存在（这里D(n)为理论上的上界），所以总的代价分析如下：
$O((D(n)+t(H))+D(n)+1+2m(H))-t(H)-2m(H)$
$=O(D(n)+t(H))-t(H)=O(D(n))=O(lgn)$

3、关键字减值与删除操作

1、关键字减值
顾名思义将堆中任意节点的值减少为某个值，具体的操作根据代码分析，伪代码实现看下图：

上面代码实现包含了三件事情，
1、如果改变的节点值小于父结点，将该结点切断（CUT）放入根表。
2、如果切断结点的父节点标记过，那么进行级联切断（CASCADING-CUT）。
3、递归的进行上面操作，知道父节点为未标记结点，或者夫结点为根结点。

代价分析：
如果该操作调用了c-1次CASCADING-CUT操作，那么该操作后，根表中结点的个数为c+t(H)，清除了c-1个标记位，但是最后一次调用CASCADING-CUT有可能又增加一个标记位。操作的代价位O©，势能的代价位：
$((t(H)+c)+2(m(H)-c+2))-(t(H)+2m(H))=4-c$
总的代价位：$O(c)+4-c=O(1)$

2、删除操作

与二项堆删除操作相同，将要删除的结点置为负无穷，执行抽取最小值操作

4、最大度数的界

引理1与证明：

引理2与证明：

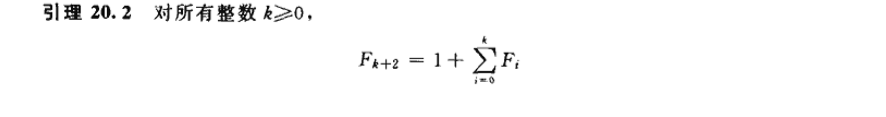
引理3与证明：

推论：