【算法学习】约瑟夫环（含公式思想总结）（Java）

一、题目描述

这个问题是以弗拉维奥·约瑟夫命名的，他是1世纪的一名犹太历史学家。他在自己的日记中写道，他和他的40个战友被罗马军队包围在洞中。他们讨论是自杀还是被俘，最终决定自杀，并以抽签的方式决定谁杀掉谁。约瑟夫斯和另外一个人是最后两个留下的人。约瑟夫斯说服了那个人，他们将向罗马军队投降，不再自杀。约瑟夫斯把他的存活归因于运气或天意，他不知道是哪一个。 ——【约瑟夫问题】维基百科

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

示例 1：
输入: n = 5, m = 3
输出: 3

示例 2：
输入: n = 10, m = 17
输出: 2

二、思路分析

思路1：模拟

通过循环链表，循环模拟数字剔除，进过测试，执行超时。

思路2：数学方法

不得不说，通过数学推导归纳得出公式后写代码，不仅简洁，执行效率也很高

递推公式：

$$f(n,m)=\{\begin{array}{ll}0,& \text{n = 0}\\ (f(n-1,m)+m)\%n& \text{n > 0}\end{array}$$

看了很多leetcode上的题解，以及约瑟夫环公式的原理推导，讲的都比较抽象，自己总结如下推导。

推导思路

以初始化有 n 个数，没 m 个剔除，使用 L(n) 代表长度为 n 的序列，设解为 F(n, m) 使用大 F 仅仅因为小 f 不太好看，并没有别的意图

1. 首先将问题定位为递归分治问题（一方面是看题解得出，另一方面据说“万物皆可分治”）
2. 既然是递归问题，就可以提出假设，假设 F(n-1) 已经算好了。
3. 基于思路2问题已经十分简单了，只需要根据 F(n-1, m) 推导出 F(n, m) 即可

针对思路3 力扣 题解中给出很多种倒推，看了好几篇不知其所以然。实际上就是为什么可以倒推和如何倒推的问题，题解中大多只给出如何倒推。

why 为什么可以倒推

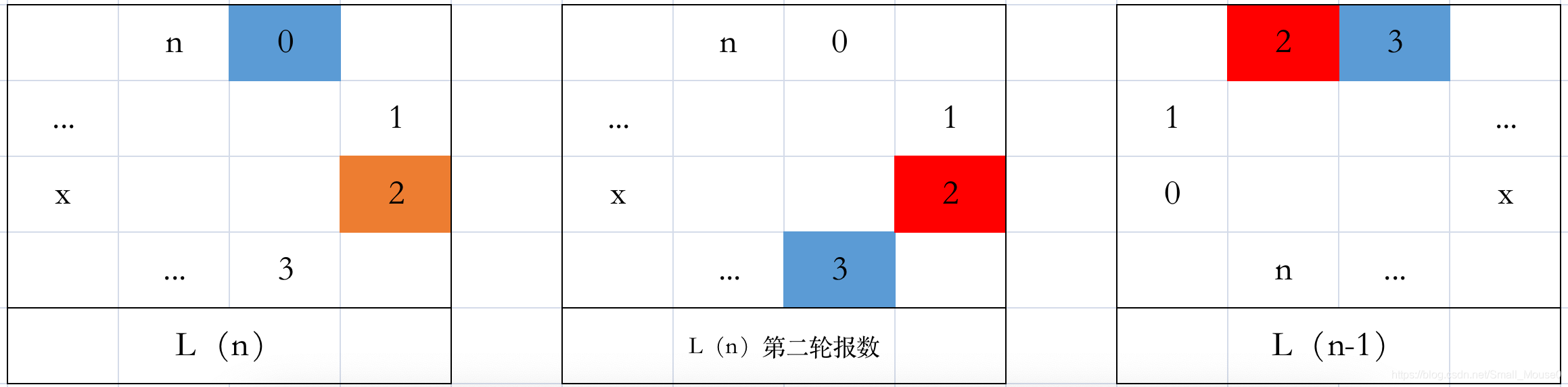
可以倒推的原因是因为 L(n-1) 的序列是从 L(n) 序列里剔除一个数，并调整顺序得来，具体如下图所示：

L(n) 实际上等价于 L(n - 1) 在最后补个 2（或者说，在L(n - 1)后补个 2， 与 L(n) 计算得出结果存在关系），因此，可以通过 L(n - 1) 序列的结果反推，L(n) 的结果。

为什么能等价呢？ 约瑟夫环，【环】，列顺序一样结果就一样，上图中 L(n - 1) 对应的环，就等价于 L(n) 删除 2 后第二轮报数 （反之，L(n-1) 补全 2 再回退一次报数，就等价于 L(n) 初始状态） 如下图所示：

how 如何倒推

明白了为什么可以倒推，如何倒推就很简单了，首先对上图中 L(n-1) 进行简化，如下图所示：

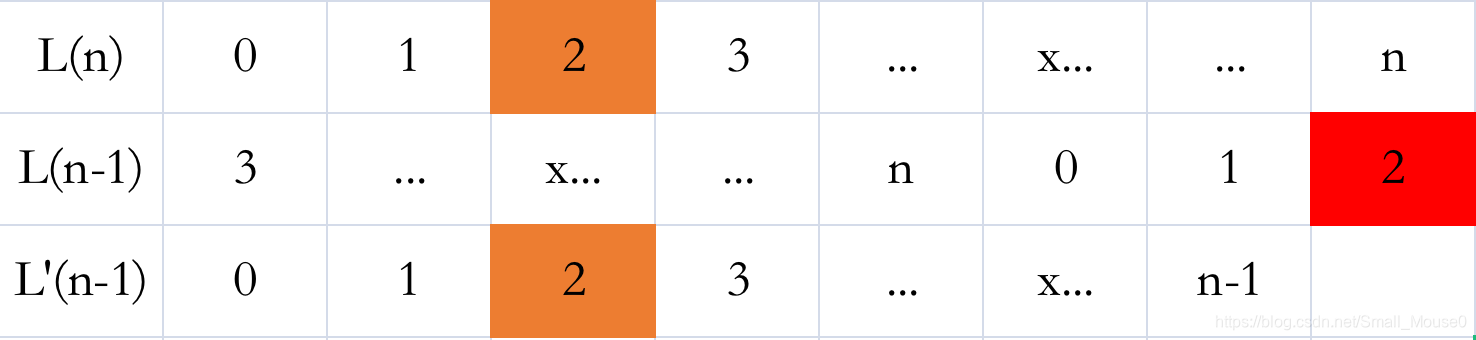
L’(n-1) 是从 0 开始新序列，L’(n-1) 的结果通过 思路2 中假设 F(n-1, m) 已经被计算出来了是 X’，即 F(n-1, m) = X’。那么，转换到 L(n-1) 中可通过 X = (X’ + m) % n 得出。首先 +m 是从 0 开始和从 3 开始的对齐， %n 是因为 m 可能大于 n。

至此，就可以推算出上文提到的公式

三、参考代码

class Solution {
    public int lastRemaining(int n, int m) {
        if(n == 1) return 0;
        
        int x = lastRemaining(n-1, m);
        return (x + m) % n;
    }
}

四、测试连接

力扣