算法基础（搜索与图论篇）

第三章：搜索与图论：

3.1 树与图的存储：

• 树是一种特殊的图，所以只需要会图的存储方式即可。在图中，无向图又是特殊的有向图，例如，对于一无向边a-b，只需要存储两条有向边即可，即a->b、b->a，故只需要会有向图的存储即可。
• 图的存储常用的有两种，分别为邻接矩阵和邻接表存储法。一般用邻接矩阵存储稠密图，即使用二维数组g[][]存储，g[a][b]表示一条由a指向b权值为g[a][b]的边。使用邻接表存储稀疏图，h[]存储每一条单链表的头结点，e[]存储每个顶点的值，ne[]存储每个顶点的邻点的下标，有时还会用w[]存储边的权重。

3.2 树与图的遍历：

3.2.1 DFS: 树的重心、n-皇后问题

注意：

• 在dfs过程中，必须恢复现场，同时对于有的问题需要进行剪枝儿，如n皇后问题。

代码实现：

public static void dfs(int u){
    st[u] = true;
    for (int i = h[u]; i != -1; i = ne[i]){
		int j = e[i];
        if (!st[j]) dfs(j);
    }
}

3.2.2 BFS: 图中点的层次、走迷宫

注意：

• 在BFS过程中没有递归，初学时要分清BFS和DFS的区别，BFS是维护一个队列。

代码实现：

static int[] q = new int[N]; // 习惯用数组模拟队列，当不能确定队列需要开多大时，最好用容器
int hh = 0, tt = 0; // 此处的tt从0开始，因为后面用到tt时，q[0]已经在队列里了，否则tt需要从-1开始
st[1] = true; // 表示1号点已经被遍历过
q[0] = 1; // 将1号点放进队列

while (hh <= tt)
{
    int t = q[hh ++]; // 取出队头元素
    
    for (int i = h[t]; i != -1; i = ne[i]) // 遍历其所有邻边
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q[++ tt] = j;
        }
    }
}

3.3 拓扑排序：有向图的拓扑排序

算法思想：

拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：

• 每个顶点出现且只出现一次
• 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面

拓扑排序利用队列，先将所有入度为0的点放进队列中（用d数组记录每个点的入度），然后从对头元素开始遍历，并让队头元素出队，对每个点的所有邻边遍历一遍，每次遍历让其入度减一，当某个点入度为0时，将其放进队列中。当队列为空时，排序结束。

代码实现：

public static boolean topSort() {
        int hh = 0, tt = -1; //数组模拟队列
        for (int i = 1; i <= n; i ++) // 先将所有入度为0的点放进队列中
            if (d[i] == 0) q[++ tt] = i;
    	// 当队列不空时，遍历队列中点的所有邻点
        while (hh <= tt) { 
            int t = q[hh ++]; // 取出队头元素
            for (int i = h[t]; i != -1; i = ne[i]){ // 遍历其所有邻点
                int j = e[i];
                d[j] --; // 每次遍历后将其入度减一
                if (d[j] == 0) q[++ tt] = j; // 当其入度为零时，将其放进队列
            }
        }
        return tt == n - 1; // 返回是否成功进行拓扑排序，当tt == n - 1时，表示已经遍历完所有点
    }

3.4 朴素Dijkstra算法O(n² + m)：Dijkstra求最短路Ⅰ

算法思想：

• 迪杰斯特拉算法只能用于求解正权图的单源路径问题。

• 迪杰斯特拉算法基于贪心，将第一个点到第一个点的距离赋值为0，其他赋值为无穷大INF，然后进行n - 1次迭代，每次在还未确定与起点最短距离的点中选出距离最小的点，然后用这个点更新其他点到起点的距离，并将这个点的状态改为已确定最短距离（即st[t] = true）。

• 有关图论的几个算法必须熟记时间复杂度，便于选择。

代码实现：

public static int dijkstra() {
        Arrays.fill(dist, INF); // INF = 0x3f3f3f3f表示无穷大
        dist[1] = 0; // 初始化起点到起点的距离为0
        for (int i = 0; i < n - 1; i ++){ // 进行n - 1次迭代，每次确定一个最小距离点
            int t = -1; // t只作为一个临时变量，用于筛选当前还未确定的距离最小的点
            for (int j = 1; j <= n; j ++){
                if (!st[j] && (t == -1 || dist[j] < dist[t])) // t == -1 表示最开始的状态，刚开始循环
                    t = j; // 寻找当前还未确定最小距离的点中的最小值
            }
            if (t == n) break; // 如果当前确定这个点是n号点，则直接退出循环
            st[t] = true; // 将t（此次确定的最小距离点）放入集合中
            for (int j = 1; j <= n; j ++)
                dist[j] = Math.min(dist[j], dist[t] + g[t][j]); //用此次确定的最小距离点更新其他点到起点的距离
        }
        if (dist[n] == INF) return -1;
        return dist[n];
    }

3.5 堆优化版Dijkstra算法O(mlogn)：Dijkstra求最短路Ⅱ

算法思想：

算法思想同朴素版，朴素版中，每次寻找当前距离最小的点时，该步骤是O(n)级别，但是如果用堆进行维护，则该步骤时间复杂度降低为O(1)，降低了瓶颈处复杂度，不过当用堆维护后，在后面需要用该点更新其他点到起点的距离时，需要对堆进行操作，所以最终时间复杂度为O(mlongn)。

代码实现：

static class PII implements Comparable<PII>{ // 手动实现C++的pair<int, int>，需要实现一个Comparable接口
        private int x, y; // x表示该点到起点的距离， y表示节点编号
        public PII(int x, int y) {
            this.x = x;
            this.y = y;
        }
        public int first() {
            return x;
        }
        public int second() {
            return y;
        }
        public int compareTo(PII p) {
            return this.x - p.x;
        }
    }

static int n, m, idx;
static final int N = 150010;
static final int INF = 0x3f3f3f3f;
static int[] h = new int[N], e = new int[N], ne = new int[N], dist = new int[N], w = new int[N]; //w表示权值
static boolean[] st = new boolean[N];
static PriorityQueue<PII> heap = new PriorityQueue();

public static void add(int a, int b, int c) {
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx ++;
}

public static int dijkstra() {
    Arrays.fill(dist, INF); //初始化距离为无穷大
    dist[1] = 0; // 将起点到起点的距离定义为0
    heap.add(new PII(0, 1)); // 将起点放进堆中(小根堆)
    while(!heap.isEmpty()){ // 当堆不空时
        PII t = heap.remove(); // 取出堆顶元素
        int vertex = t.second(), distance = t.first(); //vertex为顶点编号,diatance为当前点到起点的距离
        if (st[vertex]) continue; // 如果当前点已经确定过最小距离，则跳过该点
        st[vertex] = true; //将该点标记为已经确定最小距离
        for (int i = h[vertex]; i != -1; i = ne[i]){ // 用该点更新其他点到起点距离
            int j = e[i];
            if (dist[j] > distance + w[i]){
                dist[j] = distance + w[i];
                heap.add(new PII(dist[j], j));
            }
        } 
    }
    if (dist[n] == INF) return -1; //如果n号点到起点的距离不存在，返回-1即可（注意，dijkstra不存在负权值，无需考虑距离为1的情况，后面的bellmanFord和spfa需要考虑）
    return dist[n];
}

3.6 Bellman-Ford算法O(nm)：有边数限制的最短路

算法思想：

• Bellman-Ford算法以边为单位，进行n次迭代，每次迭代更新一遍每个点到起点的距离。Bellman-Ford算法对边的存储没什么要求，直接用一个类存储（C ++使用结构体）即可。
• 当题目规定只能经过k条边的最短路径时，只能用Bellman-Ford算法。
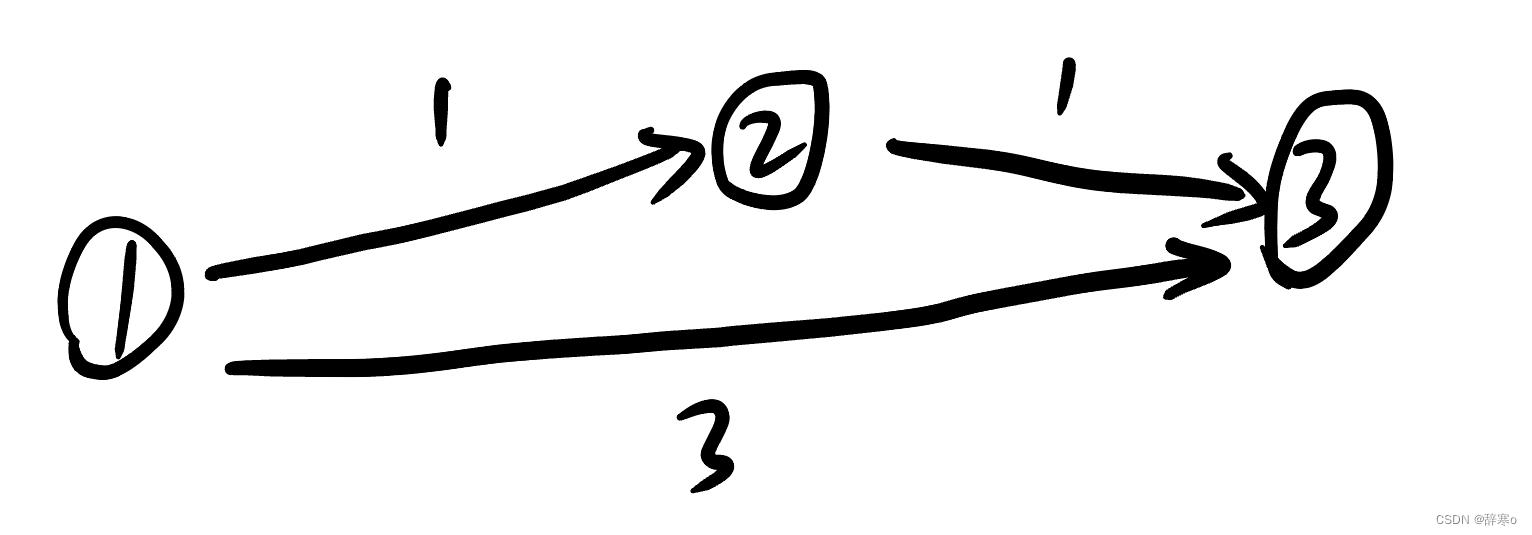
• 值得一提的是每次更新时应该用上一次迭代后的dist数组进行更新。如果用当前的dist，则在更新过几条边后，dist数组已经改变，此时再用当前的dist去更新会导致本来不能更新的点也被更新掉了。例如下图中，如果要求k = 1时，第一次迭代，会扫面一遍所有的边，当更新完编号为2这个点的距离后，dist数组已经发生变化，当扫描到2->3这条边时，dist[3]就会被更新为2，而题目要求只经过1条边，因此答案应该为3，显然不对。而我们每扫描一条边，利用上一次迭代的结果，就不会因为当前一次迭代过程中dist数组的改变而出现错误，这就是backup数组的作用。

代码实现：

static class Edge { //定义边类， a表示起点， b表示终点， w表示权值
    public int a, b, w;
    public Edge(int a, int b, int w){
        this.a = a;
        this.b = b;
        this.w = w;
    }
}

public static int bellmanFord() {
    Arrays.fill(dist, INF); // 初始化距离为无穷大
    dist[1] = 0; // 起点距离为0
    for (int i = 0; i < k; i ++){ //进行k次迭代（k为题目要求的经过k条边）
        int[] backup = Arrays.copyOf(dist, dist.length); // 拷贝上一次迭代后的dist数组
        for (int j = 0; j < m; j ++){ // 扫描每一条边
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            dist[b] = Math.min(dist[b], backup[a] + w); //更新距离
        }
    }
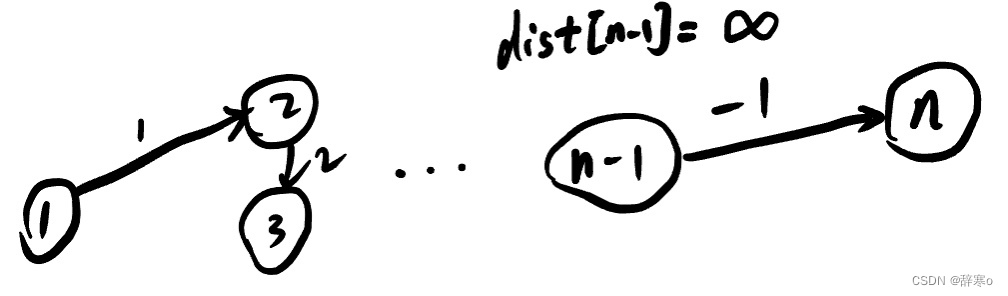
    if (dist[n] > INF / 2) flag = true; // 这种写法是为了避免下图中起点根本到达不了n这个点，而n-1这个点将dist[n]的无穷大更新为INF - 1，如下图所示
    return dist[n];
}

3.7 spfa算法O(m)/O(nm)：spfa求最短路

算法思想：

• spfa算法是对Bellman-Ford算法的优化，Bellman-Ford每次都用当前点去更新其他点到起点的距离，如果当前点的距离没有变小的话，那么这个操作就是在浪费时间，所以spfa算法在此处进行了优化，利用一个队列，每当遍历到的点距离变小时，将其放入队列中，之后会用它去更新其他点的距离。

• 并且，spfa算法一般情况下很快，很多Dijkstra能做的spfa都能做，除了阴险的出题人编造数据时，将spfa算法时间复杂度卡成O(nm)的情况，spfa算法时间复杂度一般为O(m)，最坏O(nm)。

代码实现;

public static int spfa() {
    Arrays.fill(dist, INF);
    dist[1] = 0;
    int hh = 0, tt = 0;
    q[++ tt] = 1;
    st[1] = true; // st数组表示当前的点是否在队列当中，防止存储重复的点
    while (hh <= tt) {
        int t = q[hh ++]; // 每次取出队头元素
        st[t] = false; // 取出后该点就不在队列里面
        for (int i = h[t]; i != -1; i = ne[i]){ // 用t更新其他点的距离
            int j = e[i];
            if (dist[j] > dist[t] + w[i]){ // 如果能更新，则进行更新
                dist[j] = dist[t] + w[i];
                if (!st[j]){ // 当前点不在队列当中的话，将其放进队列当中
                    q[++ tt] = j;
                    st[j] = true;
                }
            }
        }
    }
    if (dist[n] == INF) flag = true; // 当flag == true时，说明不存在路径能到达n号点，不像之前那样返回-1是因为可能路径长度为-1
    return dist[n];
}

3.8 spfa算法判负环：spfa判负环

算法思想：

该算法基于spfa算法，在该过程中增加一个cnt数组，表示从起点到该点经过了多少个点，如果某条最短路径上有n个点（除了自己），那么加上自己之后一共有n+1个点，由抽屉原理一定有两个点相同，所以存在环。并且在该背景下，这个环一定是负环，否则不会更新距离，并且不会导致死循环，因为有cnt限制，一旦cnt[j] >= n，则直接return ture。

代码实现：

static LinkedList<Integer> q = new LinkedList(); // 队列里存储节点编号
public static boolean spfa() {
    for (int i = 1; i <= n; i ++){ //之所以将所有点放进队列，是因为可能1号点根本到不了其他负环
        q.add(i);
        st[i] = true;
    }
    while (!q.isEmpty()) { // 当队列不空
        int t = q.remove(); // 队头元素出队
        st[t] = false;  // st表示当前点是否在队列中
        for (int i = h[t]; i != -1; i = ne[i]){ // 遍历其所有邻点
            int j = e[i];
            if (dist[j] > dist[t] + w[i]){
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1; // 每更新一次，将cnt[j]也更新
                if (!st[j]){
                    q.add(j); // 如果当前点不在队列中，就将其放进队列
                    st[j] = true;
                }
                if(cnt[j] >= n) return true; // 一旦发现某个点的cnt大于等于n，直接return，所以不会在负环里一直转
            }
        }
    }
    return false; // 如果一切顺利，则说明没有负环
}

3.9 Floyd算法：Floyd求最短路

算法思想：

• Floyd算法基于动态规划，使用三重循环，可以求解多源汇问题。由于Floyd算法是最短路算法的最后一个算法，所以在此进行总结。朴素Dijkstra常用于求解正权图中的稠密图，时间复杂度O(n²)、堆优化版Dijkstra常用于求解正权图中的稀疏图，时间复杂度O(mlogn)、Bellman-Ford算法常用于求解有边数限制的最短路问题，时间复杂度O(nm)、spfa算法常用于求解存在负权边的最短路问题（也可以求正权边最短路，有被卡风险）、Floyd算法常用于求解多源汇最短路问题，时间复杂度O(n³)。
• Floyd算法的代码实现较简单，理解不了先直接背过即可，后面学了DP后就好理解了。

代码实现：

public static void floyd() {
    for (int k = 1; k <= n; k ++)
        for (int i = 1; i <= n; i ++)
            for (int j = 1; j <= n; j ++)
                d[i][j] = Math.min(d[i][j], d[i][k] + d[k][j]); // d为图的邻接矩阵，Floyd算法完成后d变成每个点到其他点的最短距离矩阵
}

3.10 朴素Prim算法：prim算法求最小生成树

算法思想：

• prim算法利用是求最小生成树的一种算法，原理是从一个点出发，每次找到离集合最近的点，并将其加入到集合中，然后用这个点来更新剩下的点到集合的距离。常常用于求解稠密图的最小生成树问题。
• 集合中维护的元素就是生成树中的节点，每个点到集合的距离定义为该点到集合中任意一点距离的最小值。

代码实现：

public static int prim(){
    Arrays.fill(dist, INF);
    int res = 0; // res表示生成树中每条边的权值之和
    for (int i = 0; i < n; i ++){ //迭代n次，每次确定一个节点
        int t = -1; //t为临时变量，用于寻找到集合的最短节点
        for (int j = 1; j <= n; j ++)
            if (!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j; // 寻找到集合距离最短的节点
        if (i != 0 && dist[t] == INF) return INF; // 如果不是第一个点，并且到集合距离最短的点的距离为无穷大，则说明最小生成树不存在
        if (i != 0) res += dist[t]; // 将该条边的权值加到res中
        st[t] = true; //st表示是否加入到集合中
        for (int j = 1; j <= n; j ++) dist[j] = Math.min(dist[j], g[t][j]); //用该点更新其他点到权值的距离，g[][]最开始初始化为无穷大，为邻接矩阵
    }
    return res;
}

3.11 Kruskal算法：Kruskal算法求最小生成树

算法思想：

• Kruskal是以边为对象，首先将所有边按照权值进行排序，然后枚举每一条边，如果一条边对应的两个顶点不在同一个集合中，那么我们就将其加入到一个集合中，在枚举过程中记录一个cnt变量，每次有点加入集合中，则cnt ++，如果枚举完成之后，cnt < n - 1，则说明并不是所有点都加入集合了，故最小生成树不存在。
• 在以上过程中，判断两个点时候在集合中，可以通过之前的并查集进行维护。
• 同时，在对所有边进行排序的时候，需要重载小于号。

代码实现：

static class Edge{ // 边类
    public int a, b, w;
    public Edge(int a, int b, int w){
        this.a = a;
        this.b = b;
        this.w = w;
    }
}

public static int find(int x) { // 并查集中的find函数
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

public static int kruskal(Edge[] edgs){
    for (int i = 1; i <= m; i ++) p[i] = i; // 初始化并查集
    int res = 0, cnt = 0; // res 表示生成树的每条边权值之和
    for (int i = 0; i < m; i ++ ){ // 枚举每一条边
        int a = edgs[i].a, b = edgs[i].b, w = edgs[i].w;
        a = find(a); // 寻找a的祖宗节点
        b = find(b); // 寻找b的祖宗节点
        if (a != b){ // 如果不在一个集合当中
            res += w; 
            p[a] = b; //合并两个集合
            cnt ++;
        }
    }
	if (cnt < n - 1) return INF;
    else return res;
}

Arrays.sort(edgs, new Comparator<Edge>() { // 内部类重载小于号
    @Override
    public int compare(Edge e1, Edge e2){
        return e1.w - e2.w;
    }
});

3.12 染色法判别二分图：染色法判别二分图

算法思想：

• 二分图： 当且仅当图中不存在奇数环，可以用鸽巢原理进行证明；
• 染色法顾名思义，就是将每个点染色，染色过程中需要保证每个点与它相邻的点的颜色不同，一共两种颜色。如果在染色过程中出现矛盾，那么该图就一定不是二分图

代码实现：

public static boolean dfs(int u, int c) { // u表示当前节点编号，c表示当前颜色
    color[u] = c; // color表示颜色，0表示未染色，1和2表示两种不同颜色
    for (int i = h[u]; i != -1; i = ne[i]){ //用邻接表存储
        int j = e[i]; // j 为当前节点一个邻点的编号
        if (color[j] == 0) { // 如果这个邻点未被染色，则将其染为与u不同的另一种颜色
            if (!dfs(j, 3 - c))  // 如果染色不成功，则说明发生矛盾，直接退出
                return false;
        }
        else if (color[j] == c) return false; // 如果当前节点的一个邻点与当前节点颜色相同，则发生矛盾，直接退出
    }
    return true;
}

boolean flag = true; // 开始时flag为true，表示还没有矛盾发生
for (int i = 1; i <= n; i ++){ //枚举每一个点
    if (color[i] == 0){
        if (!dfs(i, 1)){ // 对还没有染色的节点染色
            flag = false; // 染色失败，则说明不是二分图
            break;
        }
    } 
}

3.13 匈牙利算法：二分图的最大匹配

算法思想：

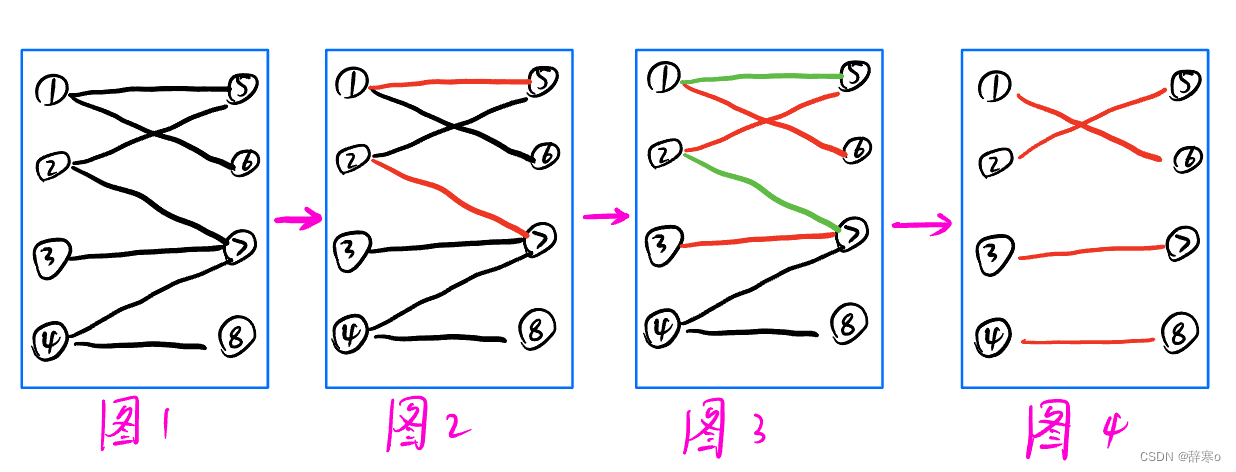
• 匈牙利算法由两位匈牙利的数学家提出，因此得名。用一个形象的例子解释，一个二分图中，所有顶点分为左右两个部分，左半部分的点与右半部分的点之间存在许多边，如果其中一条边与其他任意的边都不依附于通过一个顶点，则称这条边为一个匹配。例如图1的二分图中，图4就是该二分图的最大匹配，最大匹配数为4。
• 在整个匹配过程中，最开始1号与5号匹配，2号和7号匹配，此时没有任何问题，当3号点匹配时，发现7号点已经被匹配过了，此时，我们看看与7号匹配2号点能不能换个点匹配，而2号点的另一个可匹配点5号点被1号点匹配，我们再看1号点能不能换个点匹配，此时发现1号点还可以和6号点匹配，于是，1、2、3号点都可以匹配，如图3所示。

代码实现：

public static boolean find(int x) {
    for (int i = h[x]; i != -1; i = ne[i]){ // 枚举当前节点的所有邻点
        int j = e[i];
        if (!st[j]){ //如果j还没被考虑过
            st[j] = true; // 将j的状态设置为已考虑过
            if (match[j] == 0 || find(match[j])){ // 如果j还没有与其他点匹配，或者可以为与j匹配的点找到其他点进行匹配
                match[j] = x; // 那么就将j 这个点与x进行匹配(match[j]表示与j这个点匹配的点的节点编号)
                return true; // 匹配成功返回true
            }
        }
    }
    return false; // 如果实在匹配不了，就返回false
}

int res = 0;
for (int i = 1; i <= n1; i ++){ //左半部分点的编号为1~n1，依次枚举每个点，看能否找到匹配
    Arrays.fill(st, false); // st表示当前点是否被考虑过，并非匹配成功与否
    if (find(i)) res ++; // 如果找到匹配，最大匹配数加一
}