POJ 1003 Hangover

一、题目信息

Hangover

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 82492		Accepted: 39593

Description

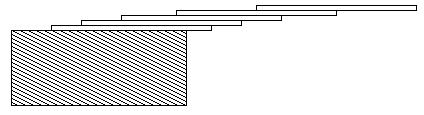
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

Input

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.

Output

For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

Sample Input

1.00
3.71
0.04
5.19
0.00

Sample Output

3 card(s)
61 card(s)
1 card(s)

二、参考代码

    水题，题目大致意思是，给出一个浮点数c，求出使得 不等式 1/2 + 1/3 + ... + 1/(n+1) >= c 成立的最小 n。既然题目已经给出上限是5.20则可以求出，当n>=300(实际小于这个数字)时候，必定可以达到上限要求。故数组长度取得300。

    此处也可以用二分查找，但是由于数组长度很短，时间上不会有太大的差别。

#include <stdio.h>
int main()
{
    float res[300] = {0,0.5},c;
    int i,num = 0;
    for (i = 2;i< 300;i++)
        res[i] = res[i-1] + 1.0/(i+1); 
    while(scanf("%f",&c) && c)
    {
        for(i = 1;i < 300;i++)
        {
            if(res[i] >= c)
            {
                printf("%d card(s)\n",i);
                break;
            }
        }
    }
    return 0;
}