图搜索算法相关研究（使用neo4j创建节点关系）

目录

图相关算法研究... 2

一．        广度优先搜索算法(BFS) 2

二．        深度优先搜索算法(DFS) 4

三．        最短路径算法(Dijkstra) 5

四．        A*算法... 7

五．        优化A*算法... 9

图相关算法研究

图是用于表示两个事物之间存在某些关系的一种结构。我们可以把事物抽象后称作节点，节点间的相互关系则称作边。所以通常在描绘一张图的时候，用一小圆圈表示节点，其间的边则使用直线或曲线来表示。图的结构是复杂的也是清晰的，我们可以用图来表示许多事物之间的实际联系以及抽象关系。用图的方式来表示某种组合或者是研究某项工程时，常常可以使得问题变得简单明了。

对于一些复杂的图，我们总是需要总结它的规律，来方便处理一些常见的问题。比如针对：如何在一个复杂关系的图中找寻从一个点到另外一个点最短路径的问题？我们该怎样解决，以及这其中有什么规律和方法方便我们以后遇到类似的问题可以快速找到答案。对于这个问题，我筛选出了几个图相关算法进行研究：广度优先搜索算法(BFS)，深度优先搜索算法(DFS)，最短路径算法(Dijkstra)，A*算法和优化A*算法等。

• 广度优先搜索算法(BFS)

对于一个算法的研究，使用一个具体的实例来表示是一个不错的方式。假设我是一名刚刚进入东南大学成贤学院读书的学生，我居住在桃园2舍（图1），位于桃园的西部，我今天早上起来发现身体不适需要去学校的医院一趟，现在的问题是我对于学校不熟悉，需要摸索到医院的路。

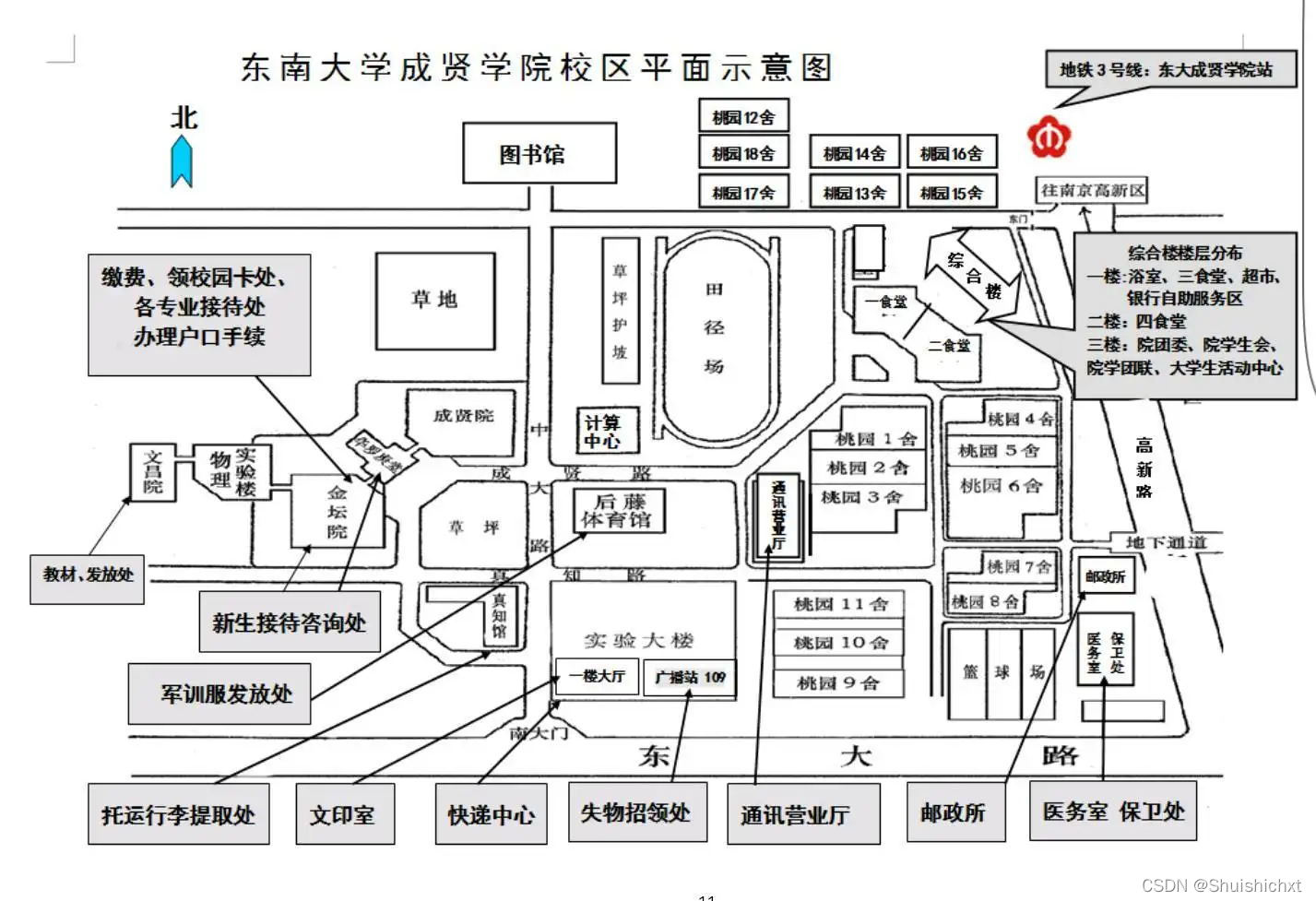
图1.东大成贤局部地图

很明显，这样的地图对于寻找目的地很不方便，这其中有太多形象化的事物，我们把标志性的建筑物抽象成一个圆圈也就是节点，把节点与节点之间不规则的路抽象成弧线也就是边，具体效果如下图（图2）。

 

图2.东大成贤局部图

现在我要从桃园西去到医院，从图上就可以很好的看出来了，但是此时我并不清楚最短的路径该怎么走。这时我采用广度优先搜索算法(BFS)来寻找路径，首先向着桃园东出发，到达桃园东以后（图3），这时有三个方向供我选择：1走向食堂，2走向邮局，3走向桃园南。

 

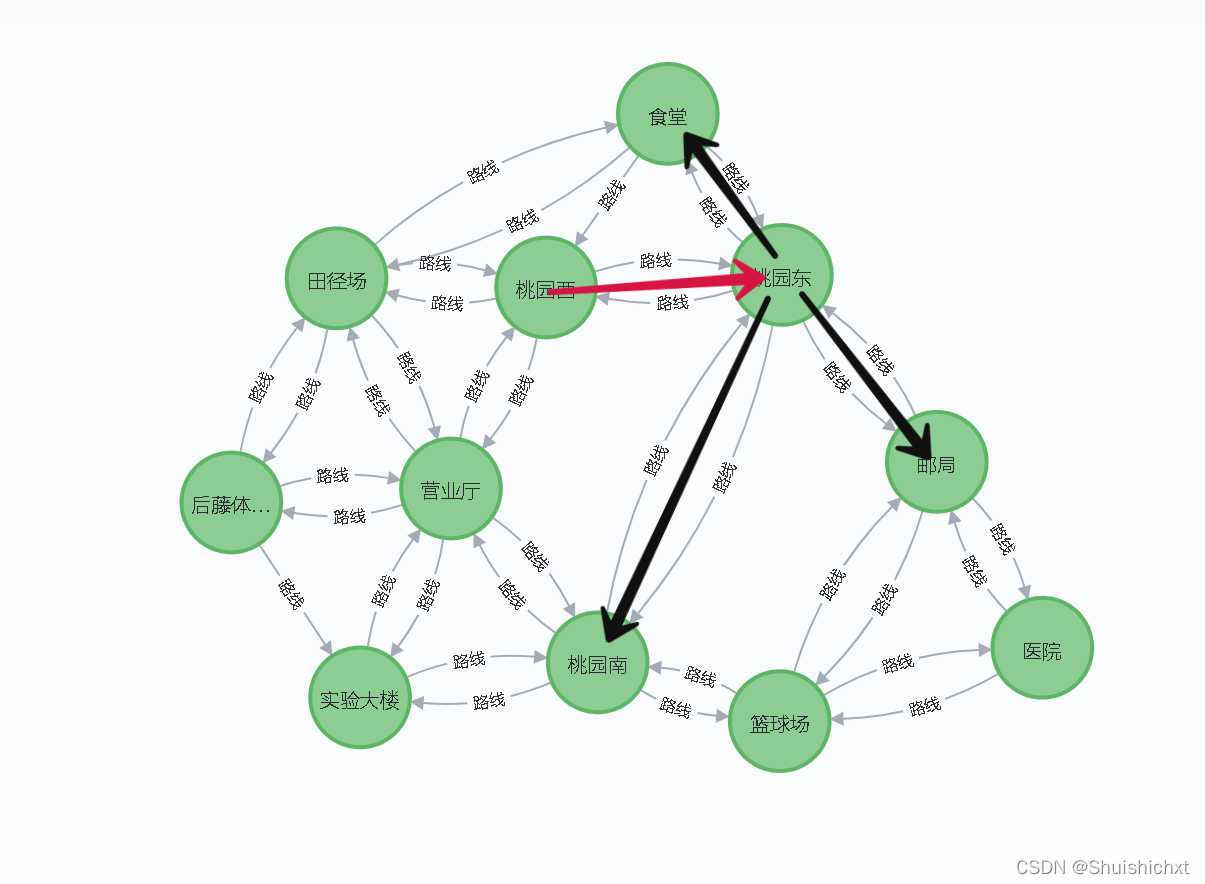
图3.东大成贤局部图

接下来，我选择走向桃园南，这时候停下来发现又多出三条路（图4）来：1走向篮球场，2走向营业厅，3走向实验大楼。并没有发现医院，于是我记下没去过的几个地点返回桃园东。

 

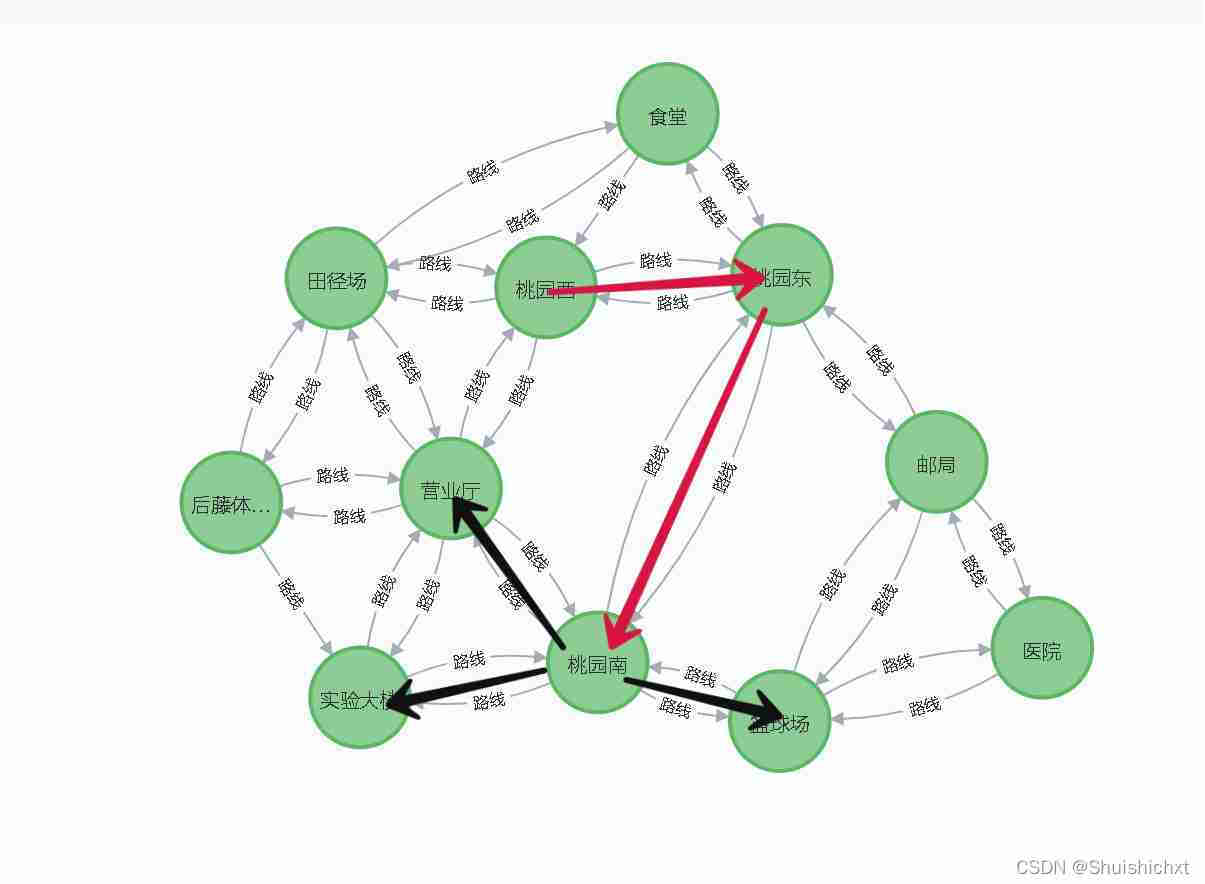
图4.东大成贤局部图

走另外一条路，走向食堂，发现又多出两条路：1走向田径场，2回到桃园西。此时我再次记下没有走过的路，返回桃园东，走向邮局。

当我一直重复上述步骤时，我需要花费大量的精力来找路径，并且可以通过这个方法把学校所有地点走个遍，但是最终一定会找到去医院的路，虽然有可能是最后一个地点才找到路，这就是广度优先搜索算法(BFS)。也许可以用伪代码来表示一下：

while(走到某一个地点){返回到上面的一个地点，假设为P点。把P点从路径中移除。for(遍历所有与P点相邻的Q点){if(Q点没有到过){把Q点添加到要走的路径中去。}}}

扩展一下，广度优先搜索算法具有完全性，意思指无论图形的种类如何，只要目标存在，则BFS一定会找到。然而，若目标不存在，且图为无限大，则BFS将不会结束一直找下去。

• 深度优先搜索算法(DFS)