本部分内容是《模式识别与机器学习》第九章,主要回答了2个问题:
1 什么是EM期望最大化算法
2 EM算法在混合模型中的应用,如高斯混合、伯努利混合以及贝叶斯混合
目录
看目录的话,本章节分为四个小节:
1 K-means聚类:作为理解EM算法的简单例子
2 高斯混合:主要是梯度固定和后验概率的概念
3 EM算法的另一观点:EM算法能够使用使用潜在变量补全数据
4 EM算法的一般形式:将EM理解为坐标上升法
介绍
- 若我们定义了关于观测值和潜在变量的联合分布,引入潜在变量和扩展空间能够从简单分布中表达出相对复杂的边缘分布。
- 最大似然估计在该空间中就理解为期望最大化算法,但最大似然法也有很大的限制。
- 第10章将会介绍更有效的变分推断的贝叶斯处理方式
K-means聚类
失真度
给定数据集{x1,...,xNx_1, ..., x_Nx1,...,xN}, 我们想要将它分割为K个簇。
根据K-means的原理,我们将使用每个簇的中心点μk\mu_kμk替代整个簇的(即数据集中的真实点,使簇中所有其他数据点到μk\mu_kμk的距离平方和为最小的那个点)
然后对每个数据点xnx_nxn,使用二元指示变量(即1-K的编码策略,one-hot)rnk∈(0,1)r_{nk} \in(0, 1)rnk∈(0,1),即rnkr_{nk}rnk=1 且rnj=1,j≠0r_{nj}=1, j \neq 0rnj=1,j̸=0,k=1,…,K,(它只有两种类型的值)用来描述该数据点所属簇。
然后介绍失真度公式如下:
J=∑n=1N∑k=1Krnk∣∣xn−μk∣∣2J=\sum^N_{n=1}\sum^K_{k=1}r_{nk}||x_n - \mu_k||^2J=n=1∑Nk=1∑Krnk∣∣xn−μk∣∣2 (式9.1)
我们计算每个簇中的数据点和作为簇中心点距离的平方和,也称为欧氏距离。
期望最大化
- 找出{rnkr_{nk}rnk}和{μk\mu_kμk}的值用于最小化失真度(式9.1)
- 迭代过程:
- 1 求期望(确定属于哪个簇):固定μk\mu_kμk,根据rnkr_{nk}rnk最小化J
rnk=(1,若k=argminj∣∣xn−μk∣∣20,其他)r_{nk}={1,若k = arg min_j||x_n - \mu_k||^2 \choose 0,其他}rnk=(0,其他1,若k=argminj∣∣xn−μk∣∣2) (式9.2)
即确定每个数据点所属簇。 - 2 最大化(重新找出簇中心点):固定rnkr_{nk}rnk,根据μk\mu_kμk最小化J
2∑n=1Nrnk(xn−μk)=02\sum^N_{n=1}r_{nk}(x_n - \mu_k) = 02n=1∑Nrnk(xn−μk)=0 (式9.3)
要使J为最小值,需要对J的函数求导,使其导数为0的点就是最小值点。
μk=∑nrnkxn ∑nrnk\mu_k=\sum_nr_{nk}x_n \ \sum_nr_{nk}μk=n∑rnkxn n∑rnk(式9.4)
即,根据第1步分好的簇来重新选择作为中心的点。
- 1 求期望(确定属于哪个簇):固定μk\mu_kμk,根据rnkr_{nk}rnk最小化J
示例
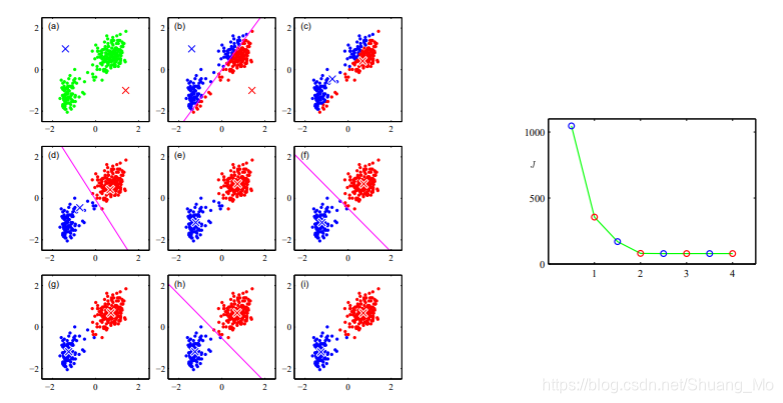
- 每个E或M步骤都会降低目标函数J的值。
- 则会收敛到局部或全局最大值。
结束
直接实现K-Means算法可能会运行缓慢,可以使用在线随机算法替代:
μknew=μkold+ηn(xn−μkold)\mu_k^{new}=\mu_k^{old} + \eta_n(x_n - \mu_k^{old})μknew=μkold+ηn(xn−μkold) (式9.5)
此处的ηn为学习速率,考虑数据点增加时仍能够单调减的情况\eta_n为学习速率,考虑数据点增加时仍能够单调减的情况ηn为学习速率,考虑数据点增加时仍能够单调减的情况
K-mediods(中心点),一般的失真度量为:
J~=∑n=1N∑k=1Krnkv(xn,μk)\widetilde{J} = \sum^N_{n=1}\sum^K_{k=1}r_{nk}\mathcal{v}(x_n, \mu_k)J=∑n=1N∑k=1Krnkv(xn,μk) (式9.6)
此处的v\mathcal{v}v(., .)表示任意相异度测量,如欧氏距离、曼哈顿距离、余弦距离等。
K-Means算法可以用于图像分割和压缩的例子:

高斯混合
潜在变量
-
潜在变量与可观测变量相反,不能直接观察,但可以通过观察到的其他变量通过数学模型进行推断得到。
-
高斯混合分布可写为一般高斯分布(正态分布)的线性叠加(第二章提过):
p(x)=∑k=1KπkN(x∣μk,∑k)p(x) = \sum^K_{k=1}\pi_k\mathcal{N}(x|\mu_k, \sum_k)p(x)=∑k=1KπkN(x∣μk,∑k) -
引入潜在变量z
- z是二元1-of-K编码变量
- 联合分布:p(x, z) = p(z) p(x|z)
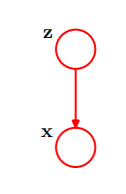
-
混合系数πk\pi_kπk有:
当使潜在变量的为1时的概率值,p(zkz_kzk = 1) = πk\pi_kπk,显然可得概率值的限制条件是:0≤πk≤10 \leq \pi_k \leq 10≤πk≤1 且 ∑kπk=1\sum_k \pi_k = 1∑kπk=1。
因为z为one-hot型变量,该分布也可以写为:p(z)=∏kπkzkp(z) = \prod_k\pi_k^{z_k}p(z)=∏kπkzk (式9.10) -
对特定潜在变量zkz_kzk,x的条件分布为:
p(x∣zk=1)=N(x∣μk,∑k)p(x | z_k = 1) = \mathcal{N}(x | \mu_k, \sum_k)p(x∣zk=1)=N(x∣μk,∑k)同理也可以写为:p(x∣z)=∏kN(x∣μk,∑k)zkp(x | z) = \prod_k\mathcal{N}(x | \mu_k, \sum_k)^z{_k}p(x∣z)=∏kN(x∣μk,∑k)zk(式9.11) -
x的边缘分布可以通过对联合分布对z的所有可能状态求和得出(结合式9.10和9.11):
p(x)=∑zp(x,z)=∑zp(z)p(x∣z)=∑kπkN(x∣μk,∑k)p(x) = \sum_zp(x, z) = \sum_zp(z)p(x | z) = \sum_k\pi_k\mathcal{N}(x | \mu_k, \sum_k)p(x)=∑zp(x,z)=∑zp(z)p(x∣z)=∑kπkN(x∣μk,∑k)
同时,x的边缘分布符合式9.7的高斯混合形式。 -
通过利用了联合概率p(x, z),使得原式9.7得到了大大的简化。
-
利用关于k的后验概率来生成观测x(贝叶斯原理):
p(zk=1∣x)=γ(zk)≡p(zk=1∣x)=p(zk=1)p(x∣zk=1)∑kp(zk=1)p(x∣zk=1)p(z_k = 1 | x) = \gamma(z_k) \equiv p(z_k = 1 | x) = \frac{p(z_k = 1) p(x | z_k = 1)} {\sum_k p(z_k = 1) p(x | z_k = 1)} p(zk=1∣x)=γ(zk)≡p(zk=1∣x)=∑kp(zk=1)p(x∣zk=1)p(zk=1)p(x∣zk=1)
=πkN(x∣μk,∑k)∑kπkN(x∣μk,∑k= \frac{\pi_k \mathcal{N}(x | \mu_k, \sum_k)} {\sum_k\pi_k\mathcal{N}(x | \mu_k, \sum_k}=∑kπkN(x∣μk,∑kπkN(x∣μk,∑k) (式9.13)
此处πk\pi_kπk表示zk=1z_k = 1zk=1的先验概率。 -
使用祖先取样生成随机样本:
首先由p(z)生成z^\hat{z}z^),随后从p(x | z^\hat{z}z^)(即高斯混合模型中生成x的值,具体见第11章。
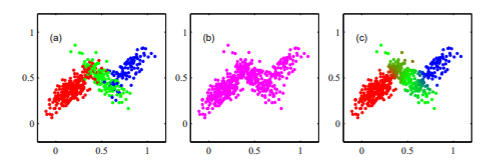
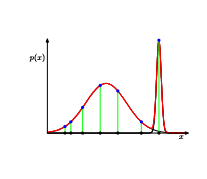
如图a,高斯部分负责生成x。
图b,边缘分布p(x)的相似样本通过从联合分布中采样并忽略z值得到。
图c,可以表示与数据点xnx_nxn联系的先验概率值γ(znk)\gamma(z_{nk})γ(znk),并绘出对应点使用红绿蓝对应γ(znk)\gamma(z_{nk})γ(znk)的k=1, 2, 3时。如γ(zn1)=1\gamma(z_{n1}) = 1γ(zn1)=1显示为红色,γ(zn2)=γ(zn3)=0.5\gamma(z_{n2}) = \gamma(z_{n3}) = 0.5γ(zn2)=γ(zn3)=0.5分别显示为绿色和蓝色。与图a相比,数据点的标记使用生成的真实component密度。
最大似然法
-
最大似然法也称为极大似然估计,是一种点估计法。基本思想是当从模型总体随机抽取n组样本观测值后,最合理的参数估计量应该是使从模型中抽取的这n组样本的观测值的概率最大。
-
log似然:
假定观测数据集{x1,...,xNx_1, ..., x_Nx1,...,xN},然后使用高斯混合对该数据建模。将该数据表示为一个N * D矩阵X,即第n行表示为xnTx_n^TxnT。相似的,对应潜在变量为N * K的矩阵Z和行znTz_n^TznT。
若假定数据点与分布相互独立,则对该独立同分布数据的高斯混合模型可以表示为下图。
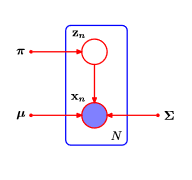
lnp(X∣π,μ,∑)=∑n=1Nln{∑k=1KπkN(x∣μk,∑k}ln p(X | \pi, \mu, \sum) = \sum_{n=1}^Nln\begin{Bmatrix}{\sum_{k=1}^K\pi_k\mathcal{N}(x | \mu_k, \sum_k}\end{Bmatrix}lnp(X∣π,μ,∑)=∑n=1Nln{∑k=1KπkN(x∣μk,∑k}(式9.14)
其中一组分为协方差矩阵∑k=σk2I,I\sum_k = \sigma_k^2I, I∑k=σk2I,I为单位矩阵。假定混合模型的第j个组分有均值μj\mu_jμj,它实际上等于其中一个数据点,即对一些n值有μj=xn\mu_j = x_nμj=xn,使得该组分坍塌于一个点。π\piπ为znz_nzn组分的混合系数。
-
奇异性
如上图所示,当混合中有至少2个组分时,其中一个含有限方差,因此可以分配有限概率给所有数据点,但当其他组分快速上升到一个特定数据点时会给log似然造成一个不断增加的相加值,则该点就称为高斯混合的奇点。
此外,对高斯混合使用最大似然法可能会导致较差的解,若使用贝叶斯方法就不会出现该问题。(第11章) -
唯一性
在k-组分混合中对一个机器学习的解,有K!K!K!个等价解。对应于有K!种方式去分配K个数据集的参数给K的组分。即,对任意参数空间中的点(非退化点),将至多有K!-1个其他点也能准确达到相同分布,称之为识别能力,当解释从模型中发现的参数时是一个重要的问题。将在第十二章详细讨论。
EM用于高斯混合
-
Dempster et al., 1977正式引入期望最大化算法
-
最大化log似然:
使lnp(X∣π,μ,∑)ln p(X | \pi, \mu, \sum)lnp(X∣π,μ,∑)的导数相关参数为0:
根据式9.14:lnp(X∣π,μ,∑)=∑n=1Nln{∑k=1KπkN(x∣μk,∑k)}ln p(X | \pi, \mu, \sum) = \sum_{n=1}^Nln\begin{Bmatrix}\sum_{k=1}^K\pi_k\mathcal{N}(x | \mu_k, \sum_k) \end{Bmatrix}lnp(X∣π,μ,∑)=∑n=1Nln{∑k=1KπkN(x∣μk,∑k)} -
对μk\mu_kμk求导有:
0=−∑n=1NπkN(x∣μk,∑k∑kπkN(x∣μk,∑k⎵γ(zk)∑k−1(xn−μk)0 = - \sum_{n=1}^N\frac{\pi_k\mathcal{N}(x | \mu_k, \sum_k} {\begin{matrix} \underbrace{ \sum_k\pi_k\mathcal{N}(x | \mu_k, \sum_k } \\ \gamma(z_k) \end{matrix}} \sum_k^{-1}(x_n - \mu_k)0=−∑n=1Nk∑πkN(x∣μk,k∑γ(zk)πkN(x∣μk,∑k∑k−1(xn−μk)
通过乘∑k−1\sum_k^{-1}∑k−1(非奇异矩阵)得,μk=1∑nγ(zk)∑nγ(zk)xn\mu_k = \frac{1}{\sum_n\gamma(z_k)}\sum_n\gamma(z_k)x_nμk=∑nγ(zk)1∑nγ(zk)xn (式9.17)
第k个高斯组分的均值μk\mu_kμk通过数据集中所有数据点的权重均值得到,而数据点xnx_nxn的权重通过先验概率γ(znk)\gamma(z_{nk})γ(znk)给定,即组分k负责生成xnx_nxn。 -
对∑k\sum_k∑k求导有:
∑k=1∑nγ(zk)∑nγ(zk)(xn−μk)(xn−μk)T\sum_k = \frac{1}{\sum_n\gamma(z_k)}\sum_n\gamma(z_k)(x_n - \mu_k)(x_n - \mu_k)^T∑k=∑nγ(zk)1∑nγ(zk)(xn−μk)(xn−μk)T (式9.19) -
对混合系数πk\pi_kπk有:
- 加入限制条件∑kπk=1\sum_k\pi_k = 1∑kπk=1
- 使用拉格朗日乘数法并最大化如下式子:
lnp(X∣π,μ,∑)+λ(∑kπk−1)ln p(X | \pi, \mu, \sum) + \lambda(\sum_k\pi_k - 1)lnp(X∣π,μ,∑)+λ(∑kπk−1)
可以得到,0=∑nN(x∣μk,∑k)∑kπkN(x∣μk,∑k)+λ0 = \sum_n \frac{\mathcal{N}(x | \mu_k, \sum_k)}{\sum_k\pi_k\mathcal{N}(x | \mu_k, \sum_k)} + \lambda0=∑n∑kπkN(x∣μk,∑k)N(x∣μk,∑k)+λ
πk=∑nγ(zk)N\pi_k = \frac{\sum_n\gamma(z_k)}{\mathcal{N}}πk=N∑nγ(zk)
此处,令λ=−N\lambda = - Nλ=−N。即第k个组分的混合系数有每个组分用于解释数据点的平均后验概率给定。
EM用于高斯混合的例子
- 没有封闭的解:因为先验概率γ(zk)依赖于参数\gamma(z_k)依赖于参数γ(zk)依赖于参数(见式9.13)
- 但上述等式也暗示了找出最大似然的简化迭代策略:
首先选择均值、协方差和混合系数的初始值,然后交替进行计算当前γ(zk)\gamma(z_k)γ(zk)以及更新参数{μk,∑k,πk\mu_k, \sum_k, \pi_kμk,∑k,πk}
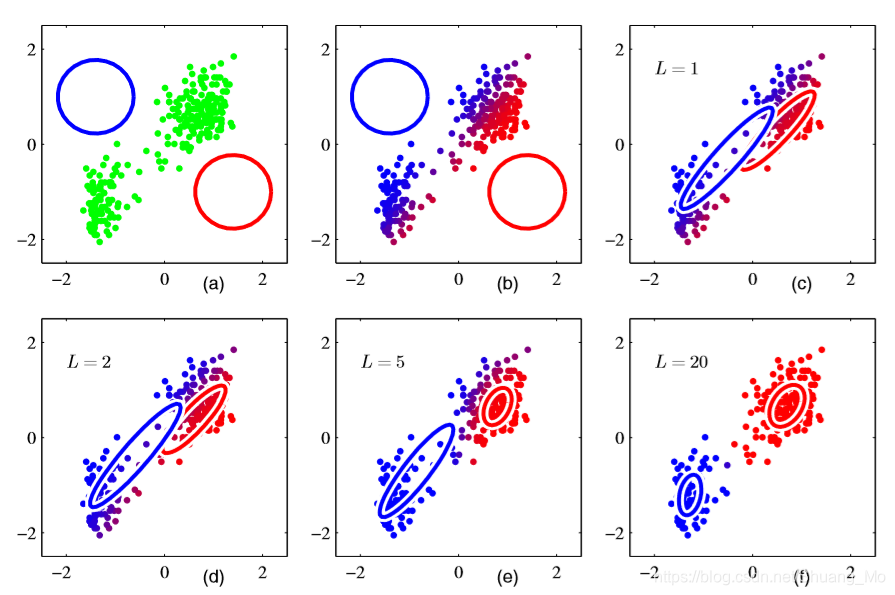
如上图,- a中以绿色展示了数据点,和混合模型的初始配置并使用蓝色和红色的圈表示标准差轮廓。
- b展示了初始化E步骤的结果,蓝色部分表示等于由蓝色组分生成的后验概率,红色同理。此外,拥有显著概率的点属于2个簇显示为紫色。
- c展示了第一次M步骤后的结果,蓝色高斯分布的均值移动到数据集的均值,概率的权重来自属于蓝色簇的每个数据点,即移动到蓝色区域的质量中心。相似的,蓝色高斯分布的协方差设置为蓝色区域的协方差。红色同理。
- d, e, f分别展示了完成2,5,20个EM完整循环后的效果,其中f更接近于收敛。
- 但相比于K-Means,高斯混合需要进行更多的迭代才能收敛,以及每次循环都得进行更多的计算。
- 因此一般先使用K-Means初始化参数,协方差矩阵可以通过从K-Means算法发现的集群中的样本协方差得到,然后混合系数可以由对应集群的数据点分数得到,均值同理。
EM用于高斯混合总结
- 初始化{μk,∑k,πk\mu_k, \sum_k, \pi_kμk,∑k,πk}并计算log似然
- E步骤计算先验概率γ(zk)\gamma(z_k)γ(zk)
- M步骤使用当前先验概率重新计算参数:
μknew=1∑nγ(zk)∑nγ(zk)xn\mu_k^{new} = \frac{1}{\sum_n\gamma(z_k)}\sum_n\gamma(z_k)x_nμknew=∑nγ(zk)1∑nγ(zk)xn
∑knew=1∑nγ(zk)∑nγ(zk)(xn−μk)(xn−μk)T\sum_k^{new} = \frac{1}{\sum_n\gamma(z_k)}\sum_n\gamma(z_k)(x_n - \mu_k)(x_n - \mu_k)^T∑knew=∑nγ(zk)1∑nγ(zk)(xn−μk)(xn−μk)T
πknew=∑nγ(zk)N\pi_k^{new} = \frac{\sum_n\gamma(z_k)}{N}πknew=N∑nγ(zk) - 计算Log似然lnp(X∣π,μ,∑)并检查收敛(返回第二步)ln p(X | \pi, \mu, \sum)并检查收敛(返回第二步)lnp(X∣π,μ,∑)并检查收敛(返回第二步)
EM的另一观点
潜在变量
- 令X为观测数据,Z为潜在变量, θ\thetaθ为所有参数
- 目标:最大化观测值的边缘log似然
lnp(X∣θ)=ln{∑zp(X,Z∣θ)}ln p(X | \theta) = ln \begin{Bmatrix}\sum_zp( X, Z | \theta) \end{Bmatrix}lnp(X∣θ)=ln{∑zp(X,Z∣θ)} (式9.29) - 但由于log求和导致优化问题,因为联合分布p(X,Z∣θ)p(X, Z | \theta)p(X,Z∣θ)属于指数族,则边缘分布p(X∣θ)p(X | \theta)p(X∣θ)并不作为求和的结果,而因为和的存在是算法不能直接作用于联合分布,导致了最大似然解的表达更加复杂。
- 假设对完整数据的直接最大化:
lnp(X,Z∣θ)ln p(X, Z | \theta)lnp(X,Z∣θ),但一般通过观测只能知道X的值,而潜在的Z只能通过后验分布p(Z∣X,θ)p(Z | X, \theta)p(Z∣X,θ)来得到,考虑潜在变量的先验分布期望值也对应于EM算法中的E步骤。接下来将进行M步骤,最大化期望。
算法
- 初始化:选择初始参数集θold\theta^{old}θold
- E步骤:使用当前参数θlod\theta^{lod}θlod来计算p(Z∣X,θold)p(Z | X, \theta^{old})p(Z∣X,θold)来找出对于一般化参数θ\thetaθ的完整数据的log似然的期望:
Q(θ,θold)=∑Zp(Z∣X,θold)lnp(X,Z∣θ)\mathcal{Q}(\theta, \theta^{old}) = \sum_Zp(Z | X, \theta^{old})ln p(X, Z | \theta)Q(θ,θold)=∑Zp(Z∣X,θold)lnp(X,Z∣θ)(式9.30) - M步骤:通过最大化式9.30来确定θnew\theta^{new}θnew
θnew=argmaxθQ(θ,θold\theta^{new} = arg max_\theta\mathcal{Q}(\theta, \theta^{old}θnew=argmaxθQ(θ,θold(式9.31) - 然后检查收敛:收敛则停止,或KaTeX parse error: Expected 'EOF', got '\the' at position 17: …theta^{old} <- \̲t̲h̲e̲^{new}并进入E步骤。
高斯混合回顾
- 对混合的每个x分配潜在变量zkz_kzk
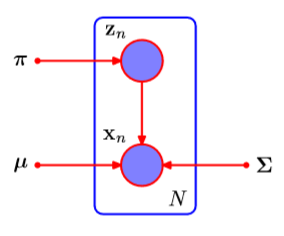
- 完整数据(log-)似然(9.36)和期望(9.40)
似然函数:
p(x,z∣θ)=∏k=1KπkzkN(x;μk,∑k)zkp(x, z | \theta) = \prod_{k=1}^K\pi_k^{z_k}\mathcal{N}(x; \mu_k, \sum_k)^{z_k}p(x,z∣θ)=∏k=1KπkzkN(x;μk,∑k)zk
取对数得:
lnp(x,z∣θ)=∑k=1Kzklnπk+lnN(x;μk,∑k)ln p(x, z | \theta) = \sum_{k=1}^Kz_k{ln \pi_k + ln \mathcal{N}(x; \mu_k, \sum_k)}lnp(x,z∣θ)=∑k=1Kzklnπk+lnN(x;μk,∑k)
对比于非完整数据的似然函数对k的求和,log型函数是可以互换的,即可以直接作用于高斯分布(它本身就是指数族的成员),这使得对最大似然法有了更容易的解。
求期望:
Q(θ)=IEz[lnp(x,z∣θ)]=∑k=1Kγ(zk)lnπk+lnN(x;μk,∑k)\mathcal{Q}(\theta) = IE_z[ln p(x, z | \theta)] = \sum_{k=1}^K\gamma(z_k){ln \pi_k + ln \mathcal{N}(x; \mu_k, \sum_k)}Q(θ)=IEz[lnp(x,z∣θ)]=∑k=1Kγ(zk)lnπk+lnN(x;μk,∑k)
上星期我们介绍了K-means算法、EM一般过程及其在高斯混合中的应用,接下来继续介绍几个EM的应用
EM算法示例
伯努利混合
- 至今我们介绍高斯分布描述的连续变量,接下来介绍不同背景的EM算法:伯努利混合描述的离散二元变量,其分布如下(该模型也称为潜在类别分析,它也为考虑离散变量的隐马可夫模型奠定了基础):
KaTeX parse error: Expected 'EOF', got '}' at position 50: …{x_i}(1 - \mu_i}̲^{(1 - x_i)}(式9.44)
即为D个二元变量(矢量),i= 1到D,每个都由参数mu(矢量)控制,独立变量xi独立于mu,显然期望为mu(矢量), 协方差为对角mu i(1 - mu i)。 - 伯努利混合还可以可以对变量相关性进行建模,也称为潜在类别分析。
- 与高斯混合相反,在本模型中没有奇点(即会使似然函数变得无穷大的点),因为$p ( x_n | \mu_k) $大于0小于1使得似然函数有上界,存在的奇点变为0。而且模型是线性且数据完整的log似然。
- 用简便的EM算法去寻找ML参数
- E步骤:计算混合组分k对于数据点xn的先验概率γ(znk)∝πkp(xn∣μk)\gamma(z_nk) \propto \pi_kp(x_n | \mu_k)γ(znk)∝πkp(xn∣μk)
- M步骤:更新参数πk=N−1∑nγ(znk)\pi_k = N^{-1}\sum_n\gamma(z_{nk})πk=N−1∑nγ(znk)和μk=(Nπk)−1∑nγ(znk)xn\mu_k = (N\pi_k)^{-1}\sum_n\gamma(z_{nk})x_nμk=(Nπk)−1∑nγ(znk)xn
- 示例:如下图,将该模型用于手写数字。数字图片已经被转换为二元矢量(将超过0.5的所有值设置为1,其他设置为0)。然后去拟合个数N=600的数据集,使用混合组分个数K=3的伯努利混合进行10次EM算法迭代来比较数字2, 3, 4。混合系数被初始化为πk=1/K\pi_k = 1 / Kπk=1/K,参数μkkj\mu_{k_{kj}}μkkj设置为从(0.25, 0.75)中随机选取的值,然后通过标准化来满足限制条件∑jμkj=1\sum_j \mu_{kj} = 1∑jμkj=1。我们可以看到3个伯努利分布的混合已经能够找出数据集中的3个簇,这3个簇也对应于3个不同的数字。
中间4个展示的数字是使用阈值0.5将灰度图转换为二元的效果,最右侧3个数字展示了混合模型中对于3个组分不同mu k(作为显示像素值)的效果,作为对比左侧的一个数字为使用单个多元伯努利分布(同样使用最大似然法)的去拟合相同数据集的效果,可见它只是简单的重复每个像素值。

贝叶斯线性回归
-
作为介绍EM应用的第三个例子,我们回顾第三章贝叶斯线性回顾的证据近似,我们是先通过计算证据,然后再设置证据表达式的导数为0,才能获得超参α\alphaα和β\betaβ的值,因此它也是一个潜在变量(潜在变量就是α\alphaα和β\betaβ)模型,我们的目标就是最大化证据函数p(t | alpha, beta),又因为参数矢量w是边缘化的,我们将其也作为潜在变量:
p(t∣w,β,X)=∏n=1NN(tn;wTϕ(xn),β−1)p(t | w, \beta, X) = \prod^N_{n=1}\mathcal{N}(t_n; w^T\phi(x_n), \beta^{-1})p(t∣w,β,X)=∏n=1NN(tn;wTϕ(xn),β−1)
p(w∣α)=N(w;0,α−1I)p(w | \alpha) = \mathcal{N}(w; 0, \alpha^{-1}I)p(w∣α)=N(w;0,α−1I)
p(t∣α,β,X)=∫p(t∣w,β)p(w∣α)dwp(t | \alpha, \beta, X) = \int p(t | w, \beta)p(w | \alpha)dwp(t∣α,β,X)=∫p(t∣w,β)p(w∣α)dw -
简便的EM算法来找出机器学习参数(α\alphaα和β\betaβ)
- E步骤:计算关于潜在变量w的先验概率
p(w∣t,α,β)=N(w;m,S),m=βSΦTt,S−1=αI+βΦTΦp(w | t, \alpha, \beta) = \mathcal{N}(w; m, S), m = \beta S\Phi^Tt, S^{-1} = \alpha I + \beta\Phi^T\Phip(w∣t,α,β)=N(w;m,S),m=βSΦTt,S−1=αI+βΦTΦ,此处
-M步骤:使用完整数据的似然估计更新参数
α−1=(1/M)(mTm+TrS)\alpha^{-1} = (1 / M)(m^Tm + Tr{S})α−1=(1/M)(mTm+TrS)
β−1=(1/N)∑n=1Ntn−mTϕ(xn)2\beta^{-1} = (1 / N)\sum_{n=1}^N{t_n - m^T\phi(x_n)}^2β−1=(1/N)∑n=1Ntn−mTϕ(xn)2
- E步骤:计算关于潜在变量w的先验概率
一般化的EM算法
总的来说,EM算法即是是找出拥有潜在变量概率模型的最大似然解的手段,现在提供一个一般化的处理过程:
- 令X为观测数据,Z为潜在变量, θ\thetaθ为参数, 联合分布为p(X, Z | theta)。
- 我们的目标:最大化观测数据的边缘log似然
lnp(X∣θ)=ln{∑Zp(X,Z∣θ)}ln p(X | \theta) = ln \begin{Bmatrix}\sum_Z p(X, Z | \theta) \end{Bmatrix}lnp(X∣θ)=ln{∑Zp(X,Z∣θ)} (式9.29) - 但问题在于最大化完整数据(即若潜在变量Z事先知道)的似然函数p(X,Z∣θ)p(X, Z | \theta)p(X,Z∣θ)简单,但最大化p(X∣θ)p(X | \theta)p(X∣θ)却很难。
- 引入关于潜在变量的分布q(Z),对任意q(Z)都可以将将似然分解为:
lnp(X∣θ)=L(q,θ)+KL(q(Z)∣∣p(Z∣X,θ)),ln p(X | \theta) = \mathcal{L}(q, \theta) + KL(q(Z) || p(Z | X, \theta)),lnp(X∣θ)=L(q,θ)+KL(q(Z)∣∣p(Z∣X,θ)),
此处KaTeX parse error: Expected group after '\frac' at end of input: …X, Z | \theta)},
KL(q∣∣p)是q(Z)和后验分布p(Z∣X,θ)的KL散度,包含Z对给定X的条件分布,式子−∑Zq(Z)lnp(Z∣X,θ)q(Z).KL(q || p)是q(Z)和后验分布p(Z | X, \theta)的KL散度,包含Z对给定X的条件分布,式子 - \sum_Z q(Z) ln \frac{p(Z | X, \theta)}{q(Z)}.KL(q∣∣p)是q(Z)和后验分布p(Z∣X,θ)的KL散度,包含Z对给定X的条件分布,式子−∑Zq(Z)lnq(Z)p(Z∣X,θ).
L(q,θ)=∑Zq(Z)lnp(X,Z∣θ)q(Z),\mathcal{L}(q, \theta) = \sum_Zq(Z)ln\frac{p(X, Z | \theta)}{q(Z)},L(q,θ)=∑Zq(Z)lnq(Z)p(X,Z∣θ),
KL(q(Z)∣∣p(Z∣X,θ))=−∑Zq(Z)lnp(Z∣X,θ)q(Z)≥0.KL(q(Z) || p(Z | X, \theta)) = - \sum_Zq(Z)ln\frac{p(Z | X, \theta)}{q(Z)} \geq 0.KL(q(Z)∣∣p(Z∣X,θ))=−∑Zq(Z)lnq(Z)p(Z∣X,θ)≥0.
EM边界
- L(q,θ)\mathcal{L}(q, \theta)L(q,θ)是该数据log似然的下界,式子如下
- −L(q,θ)- \mathcal{L}(q, \theta)−L(q,θ)称为变分自由能,
L(q,θ)=lnp(X∣θ)−KL(q(Z)∣∣p(Z∣X,θ)≤lnp(X∣θ)\mathcal{L}(q, \theta) = ln p(X | \theta) - KL(q(Z) || p(Z | X, \theta) \leq ln p(X | \theta)L(q,θ)=lnp(X∣θ)−KL(q(Z)∣∣p(Z∣X,θ)≤lnp(X∣θ)
- −L(q,θ)- \mathcal{L}(q, \theta)−L(q,θ)称为变分自由能,
- EM算法对L\mathcal{L}L进行了坐标上升法
- E步骤:固定θ\thetaθ,使用q去最大化L
- M步骤:固定q,使用θ\thetaθ去最大化L
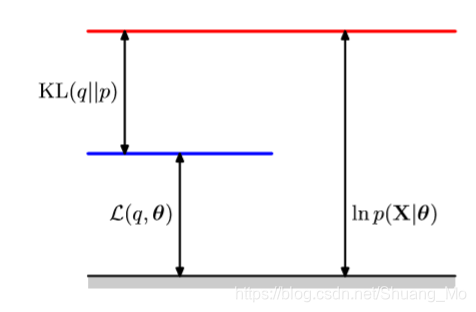
如下图所示为分解结果,此处q(Z)可以为任意分布,因为KL散度满足条件KL(q∣∣p)≥0KL(q || p) \geq 0KL(q∣∣p)≥0,则L(q,θ)\mathcal{L}(q, \theta)L(q,θ)为似然函数lnp(X∣θ)ln p(X | \theta)lnp(X∣θ)的下界:
E步骤
- E步骤:固定θ\thetaθ,使用q去最大化L(q,θ)\mathcal{L}(q, \theta)L(q,θ)
L(q,θ)=lnp(X∣θ)−KL(q(Z)∣∣p(Z∣X,θ))\mathcal{L}(q, \theta) = ln p(X | \theta) - KL(q(Z) || p(Z | X, \theta))L(q,θ)=lnp(X∣θ)−KL(q(Z)∣∣p(Z∣X,θ)) - 使用q(Z)<−p(Z∣X,θ)q(Z) <- p(Z | X, \theta)q(Z)<−p(Z∣X,θ)最大化L\mathcal{L}L
如下图为EM算法的E步骤,q分布设置等于对当前参数θold\theta^{old}θold的后验分布,这使得KL散度消失,进而下界移动到log似然函数的相同值。
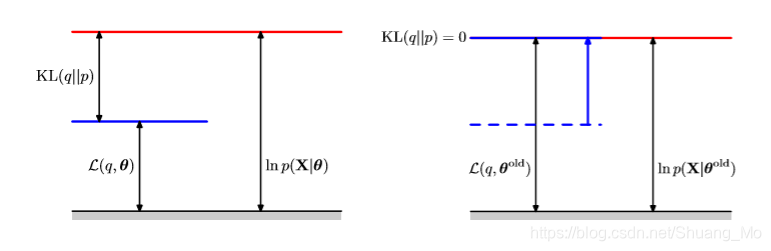
如下图,展示了EM算法的M步骤,分布q(Z)保持固定,然后下界L(q, theta)对应修正值theta new的theta参数矢量的最大值。因为KL散度为非负值,这将造成log似然ln p(X | theta)至少增加到下界。
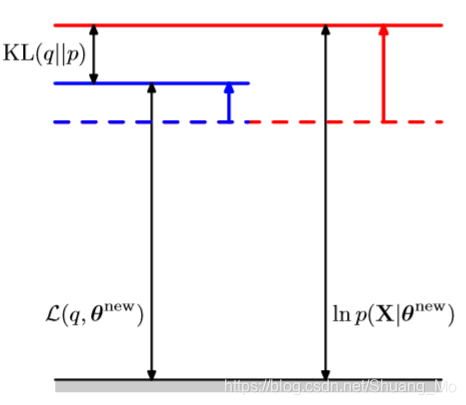
参数空间的图片
- E步骤重置边界L(q,θ)为lnp(X∣θ)(θ=θ(old))\mathcal{L}(q, \theta)为ln p(X | \theta) ( \theta = \theta^(old))L(q,θ)为lnp(X∣θ)(θ=θ(old)),它即是:
- 固定在θ=θold\theta = \theta^{old}θ=θold
- 正切于点θ=θold\theta = \theta^{old}θ=θold
- 对指数族混合成分在θ\thetaθ是凸的
如下图所示,多次计算log似然函数对当前参数值的下界然后最大化该边界去获得新的参数值(为似然函数和下界的切点):
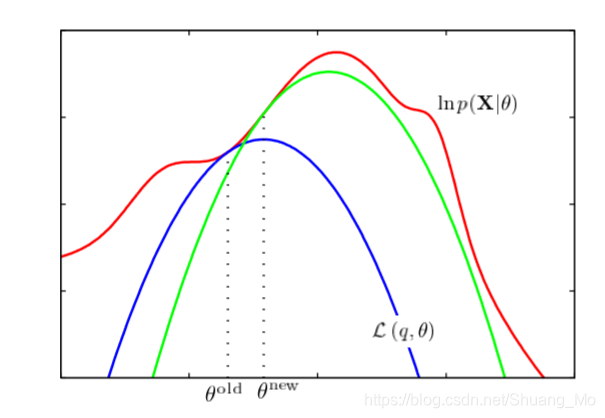
最后的思考
- L(q,θ)\mathcal{L}(q, \theta)L(q,θ)的(局部)最大值取决于 lnp(X∣θ)ln p(X | \theta)lnp(X∣θ)
- EM收敛于似然(局部最大值)
- 对L(q,θ)\mathcal{L}(q, \theta)L(q,θ)的局部上升法,并在E步骤之后L=lnp(X∣θ)\mathcal{L} = ln p(X | \theta)L=lnp(X∣θ)
- 多种策略来优化边界:
- 归纳的EM:从最大化放松M步骤以提升L\mathcal{L}L
- 期望条件最大化:M步骤轮流使用不同参数组合最大化
- 增加EM:对每个数据点进行E步骤,进而增加了M步骤
- 变分EM:从最大化放松E步骤来提升L\mathcal{L}L
- E步骤之后不再使L=lnp(X∣θ)\mathcal{L} = ln p(X | \theta)L=lnp(X∣θ)
- 同样应用于MAP估计 p(θ∣X)=p(θ)p(X∣θ)/p(X)p(\theta | X) = p(\theta)p(X | \theta) / p(X)p(θ∣X)=p(θ)p(X∣θ)/p(X)
- 边界第二项:lnp(θ∣X)≥lnp(θ)+L(q,θ)−lnp(X)ln p(\theta | X) \geq ln p(\theta) + \mathcal{L}(q, \theta) - ln p(X)lnp(θ∣X)≥lnp(θ)+L(q,θ)−lnp(X)
MAP是Maximum posterior即最大后验。
- 边界第二项:lnp(θ∣X)≥lnp(θ)+L(q,θ)−lnp(X)ln p(\theta | X) \geq ln p(\theta) + \mathcal{L}(q, \theta) - ln p(X)lnp(θ∣X)≥lnp(θ)+L(q,θ)−lnp(X)






















 1566
1566










