365天挑战LeetCode1000题——Day 019 动态规划 17-优快云博客

本文链接：https://blog.youkuaiyun.com/ShowMeTheCod3/article/details/125605033

本文提供两种算法的代码实现：最长回文子串（LeetCode 5.）及最长回文子序列（LeetCode 516.）。通过动态规划解决字符串问题，给出详细的代码逻辑与注释，帮助理解如何寻找字符串中最长的回文结构。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

5. 最长回文子串（114）
- 代码实现（思路看题解）
516. 最长回文子序列（115）
- 代码实现（首刷自解）

5. 最长回文子串（114）

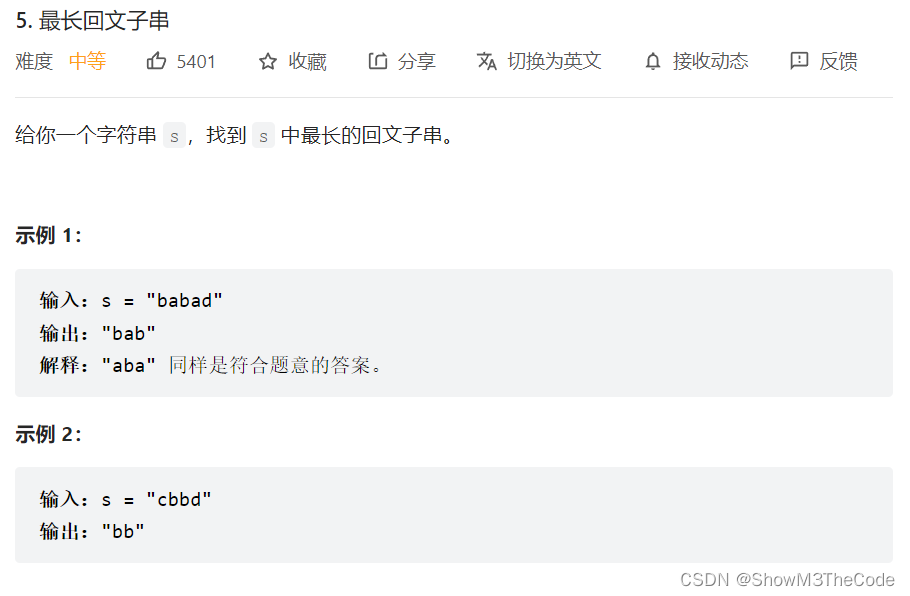
在这里插入图片描述

代码实现（思路看题解）

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n, 1));
        // int maxLen = 1;
        // the first loop is based on len of the substr
        for (int k = 2; k <= n; k++) {
            // the second loop is based on cols
            for (int i = 0; i <= n - k; i++) {
                // number of row
                int j = i + k - 1;
                // if k is 2, judge wheter two characters are equal
                if (k == 2 && s[i] == s[j]) dp[i][j] = 2;
                // else
                else {
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                    if (s[i] == s[j]) {
                        dp[i][j] = max(dp[i + 1][j - 1] + 2, dp[i][j]);
                    }
                }
                // maxLen = max(maxLen, dp[i][j]);
            }
        }
        return dp[0][n - 1];        
    }
};

516. 最长回文子序列（115）

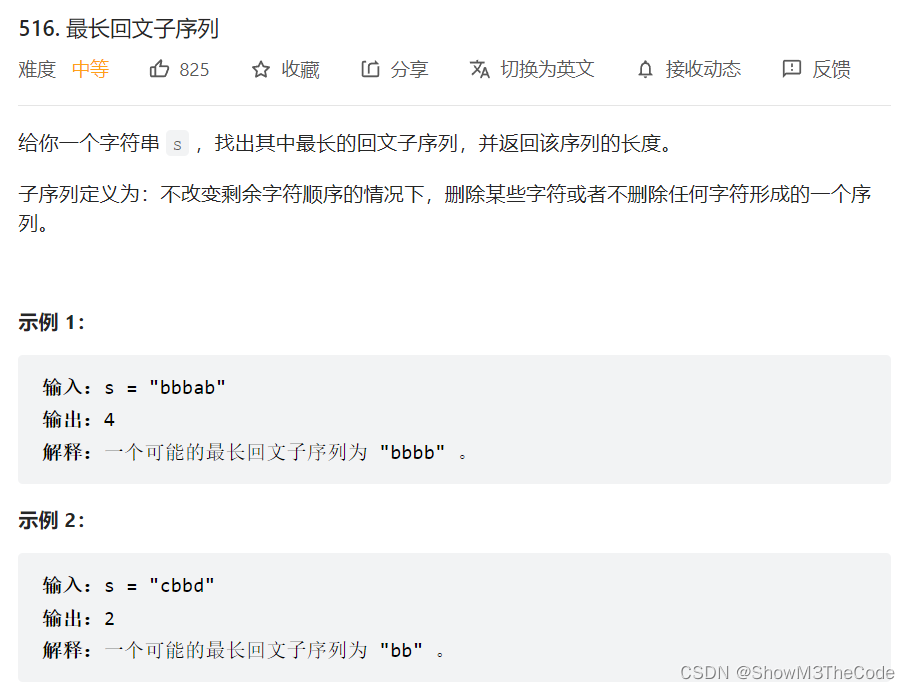
在这里插入图片描述

代码实现（首刷自解）

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n, 1));
        // int maxLen = 1;
        // the first loop is based on len of the substr
        for (int k = 2; k <= n; k++) {
            // the second loop is based on cols
            for (int i = 0; i <= n - k; i++) {
                // number of row
                int j = i + k - 1;
                // if k is 2, judge wheter two characters are equal
                if (k == 2 && s[i] == s[j]) dp[i][j] = 2;
                // else
                else {
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                    if (s[i] == s[j]) {
                        dp[i][j] = max(dp[i + 1][j - 1] + 2, dp[i][j]);
                    }
                }
                // maxLen = max(maxLen, dp[i][j]);
            }
        }
        return dp[0][n - 1];        
    }
};