Leetcode--Java--559. N 叉树的最大深度

本文链接：https://blog.youkuaiyun.com/Sherlock_Obama/article/details/121449743

本文介绍了如何求解N叉树的最大深度问题，通过BFS层序遍历和DFS递归两种方法进行解析，详细解释了算法思路并提供了相应的Java代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

给定一个 N 叉树，找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
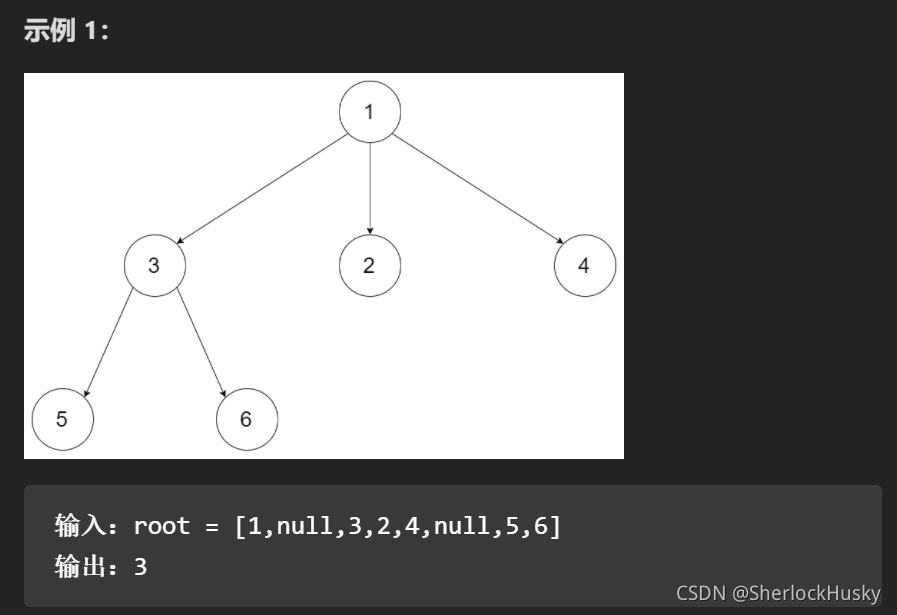
N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

样例描述

在这里插入图片描述

思路

BFS 层序遍历 / DFS 递归

在层序遍历过程中，每次队列弹出完所有元素就层数加一。
加入队列时，扫描完该结点的所有孩子结点。

DFS 递归

从root所有子节点中取最大深度，并在此基础上加一（加上root结点的深度）

代码

BFS

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public int maxDepth(Node root) {
         int level = 0;
         Deque<Node> q = new LinkedList<>();
         if (root != null) {
             q.offer(root);
         }
         while (!q.isEmpty()) {
             int size = q.size();
             //层数加一
             level ++;
             for (int i = 0; i < size; i ++ ) {
                Node node = q.poll();
                //只要有孩子就加入队列
                for (Node child: node.children) {
                    if (child != null) {
                        q.offer(child);
                    }
                }
             }
         }
         return level;

    }
}

DFS

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public int maxDepth(Node root) {
        //到空就返回0
        if (root == null) return 0;
        int res = 0;
        //统计所有子节点的最大深度
        for (Node child: root.children) {
            res = Math.max(res, maxDepth(child));
        }
        //返回（加上root后）的深度
        return res + 1;

    }
}