杭电2045 不容易系列之(3)—— LELE的RPG难题

杭电2045 http://acm.hdu.edu.cn/showproblem.php?pid=2045

 

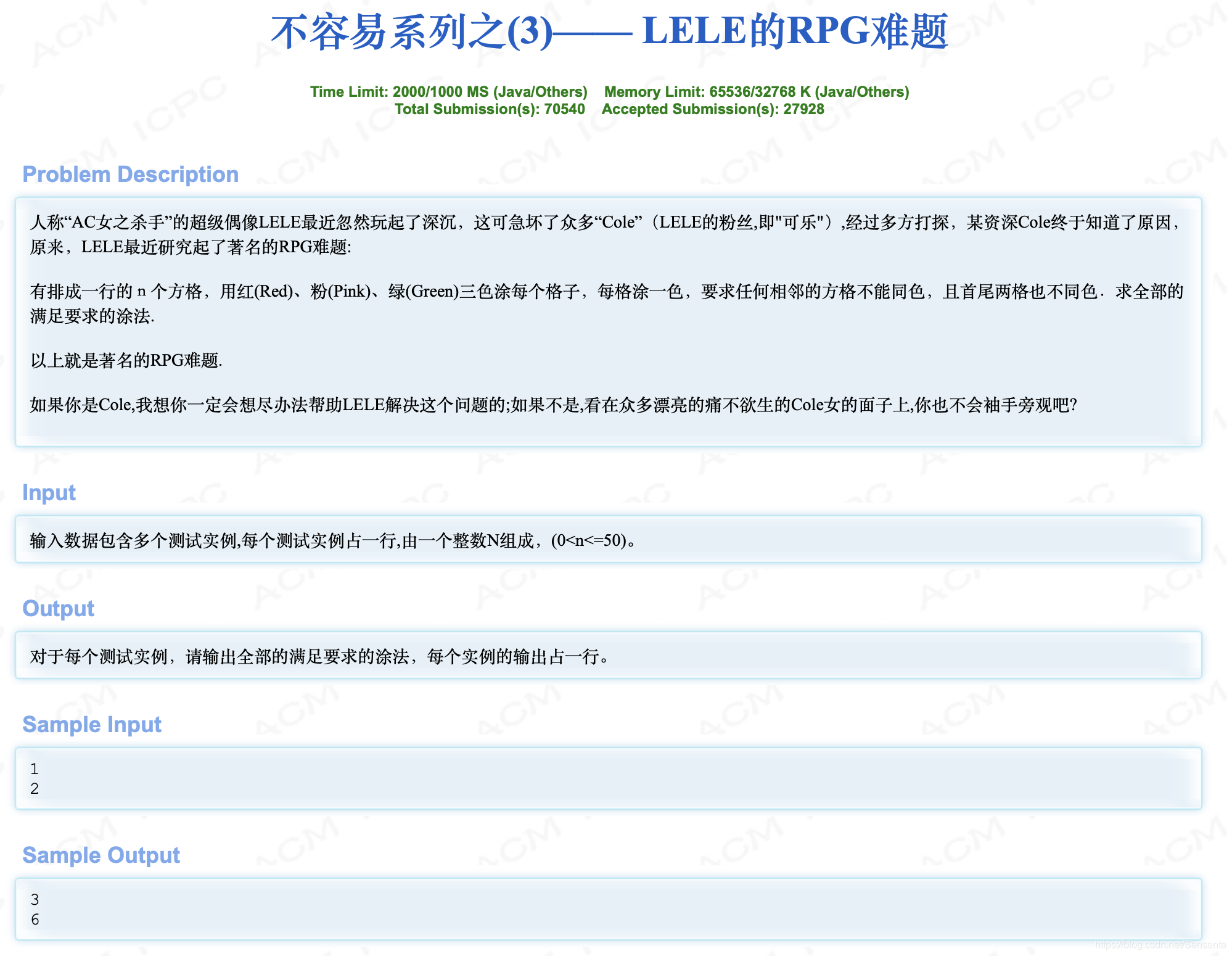
题目大意：

还是递推，一开始以为涂色问题想找规律来着。。思路还是要对才能做出来。

我们先考虑第n-1个方块。

它可以与第一个方块颜色相同，这样最后一个方块只能涂一种颜色。总方案数就是f(n-1);

再考虑第n-2个方块。

此时第n-2个方块需要与第一个方块颜色不同，（相同即为第一种考虑），此时第n个方块就有2种涂法。总方案数即2 * f(n-2)

因此得到递推式：

f(n)=f(n-1)+2*f(n-2);

 

 

AC代码：

#include <iostream>
using namespace std;
long long a[100];
int n;
int main() {
    while(cin>>n) {
        a[1]=3;
        a[2]=6;
        a[3]=6;
        for(int i=4;i<=n;i++) {
            a[i]=a[i-1]+2*a[i-2];
        }
        cout<<a[n]<<endl;
    }
    return 0;
}