异或以及其相关应用

先举一个运用到异或的题目来深刻理解一下异或的内涵和在何种情况下应用其会使问题处理简便：

1-1000放在含有1001个元素的数组中，只有唯一的一个元素值重复，其它均只出现
一次。每个数组元素只能访问一次，设计一个算法，将它找出来；不用辅助存储空
间，能否设计一个算法实现？

解法一、显然已经有人提出了一个比较精彩的解法，将所有数加起来，减去1+2+...+1000的和。
这个算法已经足够完美了，相信出题者的标准答案也就是这个算法，唯一的问题是，如果数列过大，则可能会导致溢出。
解法二、异或就没有这个问题，并且性能更好。
将所有的数全部异或，得到的结果与1^2^3^...^1000的结果进行异或，得到的结果就是重复数。

但是这个算法虽然很简单，但证明起来并不是一件容易的事情。这与异或运算的几个特性有关系。
首先是异或运算满足交换律、结合律。
所以，1^2^...^n^...^n^...^1000，无论这两个n出现在什么位置，都可以转换成为1^2^...^1000^(n^n)的形式。

其次，对于任何数x，都有x^x=0，x^0=x。
所以1^2^...^n^...^n^...^1000 = 1^2^...^1000^(n^n)= 1^2^...^1000^0 = 1^2^...^1000（即序列中除了n的所有数的异或）。

令，1^2^...^1000（序列中不包含n）的结果为T
则1^2^...^1000（序列中包含n）的结果就是T^n。
T^(T^n)=n。
所以，将所有的数全部异或，得到的结果与1^2^3^...^1000的结果进行异或，得到的结果就是重复数。

当然有人会说，1+2+...+1000的结果有高斯定律可以快速计算，但实际上1^2^...^1000的结果也是有规律的，算法比高斯定律还该简单的多。

什么是异或，简单的说：

0^0=0

1^0=1

1^1=0

并且有A^0=A   A^A=0

并且B^A^A=B  因为B^A^A=B^(A^A)=B^0=B

然后可以利用他来交换AB的值 只要这样

A^=B

B^=A

A^=B

还有就是使用异或运算实现两数交换：

通常我们实现两数交换不得不引入一个临时变量temp作为媒介，而使用异或运算也能实现同样的功能，甚至无需使用临时变量。

这是一个通常的做法：

int main(){
	int a=1,b=2,temp;
	temp=a;
	a=b;
	b=temp;
	printf("%d,%d\n",a,b);
	return 0;
}

关于异或(Exclusive OR)

Wikipedia解释

在数位逻辑中，逻辑算符互斥或闸（exclusive or）是对两个运算元的一种逻辑分析类型，符号为XOR或EOR或⊕。与一般的或闸OR不同，当两两数值相同为真..而有一数值不同时为否..

两个运算元（命题）：A与B的异或一般写成A异或B，或者写成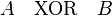、、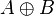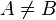等等。在C语言中，写作A^B。

异或真值表

A	B	A^B
0	0	0
0	1	1
1	0	1
1	1	0

异或的小例子

假设a为二进制数01，b为二进制数10，a^b的结果为11并将其存储在变量c中，经过反复的测试，于是发现以下的规律：

11^01=10
11^10=01

c^a=b;
c^b=a;

可以很惊奇的发现，将两数异或的结果与其中一数再进行异或，可以得到另一个数。
原理很简单，两数异或的结果保存了两个数上每一个二进制位不同或相同的信息，如果相应的二进制位不同，就标志为1，如果相同，则标志为0。

由于任意一个二进制位与1异或有这样一个特性：

0^1=1
1^1=0

即与1异或后，都将自己转换成相反的位

这样，我们就使用异或运算交换了两数

   12(001100)

^ 34(100010)

-------------------

         101110

101110 ^ 001100=100010

101100 ^ 100010=001100

int main(){
    int a=12,b=34,temp;
    printf("Original result: a=%d,b=%d\n",a,b);
    temp=a^b;
    a=temp^a;
    b=temp^b;
    printf("Transformed result: a=%d,b=%d\n",a,b);
    return 0;
}

//////////////////////// result //////////////////////////
Original result: a=12,b=34

Transformed result: a=34,b=12

但是使用这种方法似乎与使用临时变量没有什么区别？

其实不然，通过简单分析可以发现临时变量的值在整个过程中并没有发生变化，因此也可以无需设置临时变量。

a=a^b^a;
b=a^b^b;

于是可以使用第三种方法，将a设置为临时变量

a=a^b;
b=b^a;
a=b^a;

还可以写得更简洁一点：

a^=b^=a^=b;