code:https://github.com/Aiden0526/Aristotle
来源:ACL 2025
Abstract
在大型语言模型(llm)的背景下,当前的高级推理方法在各种推理任务中取得了令人印象深刻的进步。然而,当涉及到逻辑推理任务时,主要的挑战仍然是效能和效率。这源于这样一个事实,即这些系统在整个推理过程(如分解、搜索和解析)中未能充分利用逻辑任务的固有结构。为了解决这个问题,我们提出了一个逻辑完备的推理框架,即亚里士多德,它包含三个关键组件:逻辑分解器Logical Decomposer、逻辑搜索路由器 Logical Search Router和逻辑解析器 Logical Resolver。
在我们的框架中,符号表达式和逻辑规则被全面集成到整个推理过程 entire reasoning process中,显著缓解了逻辑推理的瓶颈,即降低子任务复杂性reducing sub-task complexity、最小化搜索错误minimizing search errors和解决逻辑矛盾resolving logical contradictions。
在几个数据集上的实验结果表明,亚里士多德在准确性和效率方面始终优于最先进的推理框架,特别是在复杂的逻辑推理场景中表现出色。

Related works
Chain-of- Thought
the most groundbreaking works is the Chain-of-Thought (CoT) (Wei et al., 2022), which breaks down complex problems into smaller sub-problems, solving them step by step. urther research has built on this founda-tion by closely emulating human cognitive patterns, introducing more advanced approaches, such as Least-to-Most (Zhou et al., 2023), Tree-of-Thought (ToT) (Yao et al., 2023), Graph-of-Thought (GoT)(Besta et al., 2023), and Plan-and-Solve (Wang et al., 2023a), which have achieved progressively better results on reasoning benchmarks.
In summary, successful LLM-based reasoning methods generally involve three key modules (Huang and Chang, 2023; Li et al., 2024): problem decomposition, path searching, and problem resolution.
logical reasoning
In recent years, numerous studies have inves-tigated how to integrate LLMs into logical reason-ing. For example, some methods (Pan et al., 2023;Gao et al., 2023) use LLMs to translate textual prob-lems into symbolic expressions, which are then addressed by external logic solvers. Subsequent work, such as SymbCoT (Xu et al., 2024), suggests that LLMs themselves can handle both symbolic translation and logic resolution, thus avoiding po-tential information loss caused when using external solvers.
cot线性的比较简陋?
While SymbCoT has achieved state-of-the-art (SoTA) performance, the inherent simplicity of CoT’s linear reasoning process leaves consider-able room for further improvement in LLM-based logical reasoning.
但是复杂的效率又太低了↓
(Yao et al., 2023; Besta et al., 2023; Zhang et al., 2023) has applied sophisticated general-purpose reasoning methods (e.g., ToT, GoT) directly to logical reasoning tasks.( largely overlook the inherent structure of logical tasks and fail to ef-fectively integrate logical rules)
Challenge
Efficacy — Faulty Logical Reasoning
问题:当前LLM在分解逻辑问题时往往基于语言表层关系而非真实的逻辑结构,导致:
-
子问题之间断裂,破坏逻辑链条;
-
在搜索过程中依赖不可靠的评估器,传播错误路径;
-
解决阶段使用简单prompt引导,常嵌入逻辑错误,产生大量错误节点。
后果:错误在整个推理链中传播,最终导致整体推理失败。实验表明,用SoTA方法直接应用于逻辑任务,会产生较高的推理(28.4%)和搜索(15.0%)错误率。
Efficiency — Wasteful and Redundant Computation
问题:现有方法在效率方面存在严重浪费,表现为:
-
大量生成无效或错误节点,浪费计算资源;
-
不可靠的评估器引导错误路径,导致冗余搜索和重复探索;
-
缺乏结构引导,使推理不集中、低效。
后果:效率低下,限制了逻辑推理系统在实际场景中的应用价值。
Contribution
-
A logic-aware reasoning framework (Aristotle):
We propose Aristotle, a novel reasoning framework that fully integrates symbolic logic into all three stages of the reasoning process—decomposition, search, and resolution—enabling more coherent and reliable logical reasoning with LLMs.
Introduce a Logical Decomposer that breaks down the original prob-lem into smaller and simpler components based on its logical structure, reducing the complexity of logical tasks. We then devise a Logical Search Router, which leverages proof by contradiction to directly search for logical inconsistencies, thereby reducing search errors from unreliable evaluators and minimizing the number of steps required by existing methods. Finally, we develop a Logical Resolver, which rigorously resolves logical con-tradictions at each reasoning step, guided by the Logical Search Router.
-
Superior empirical performance:
Aristotle outperforms state-of-the-art baselines by 4.5% with GPT-4 and 5.4% with GPT-4o on multiple logical reasoning benchmarks, with further gains in complex scenarios (e.g., deeper or more intricate logical chains). -
First full integration of symbolic logic into LLM reasoning:
To our knowledge, this is the first framework to successfully incorporate symbolic logic expressions into every stage of an LLM-based reasoning pipeline, demonstrating that LLMs can achieve complete and rigorous logical reasoning when properly guided.
Method
Architecture
Given a set of premises P = {p1, p2, . . . , pn}, where each pi represents a logical statement, a reasoner should derive an answer A regarding a given statement S.
The possible answer is true (T ), false (F ), unknown (U), or self-contradictory (SD).1 The formal definition of each answer can be found in Eq. (1).
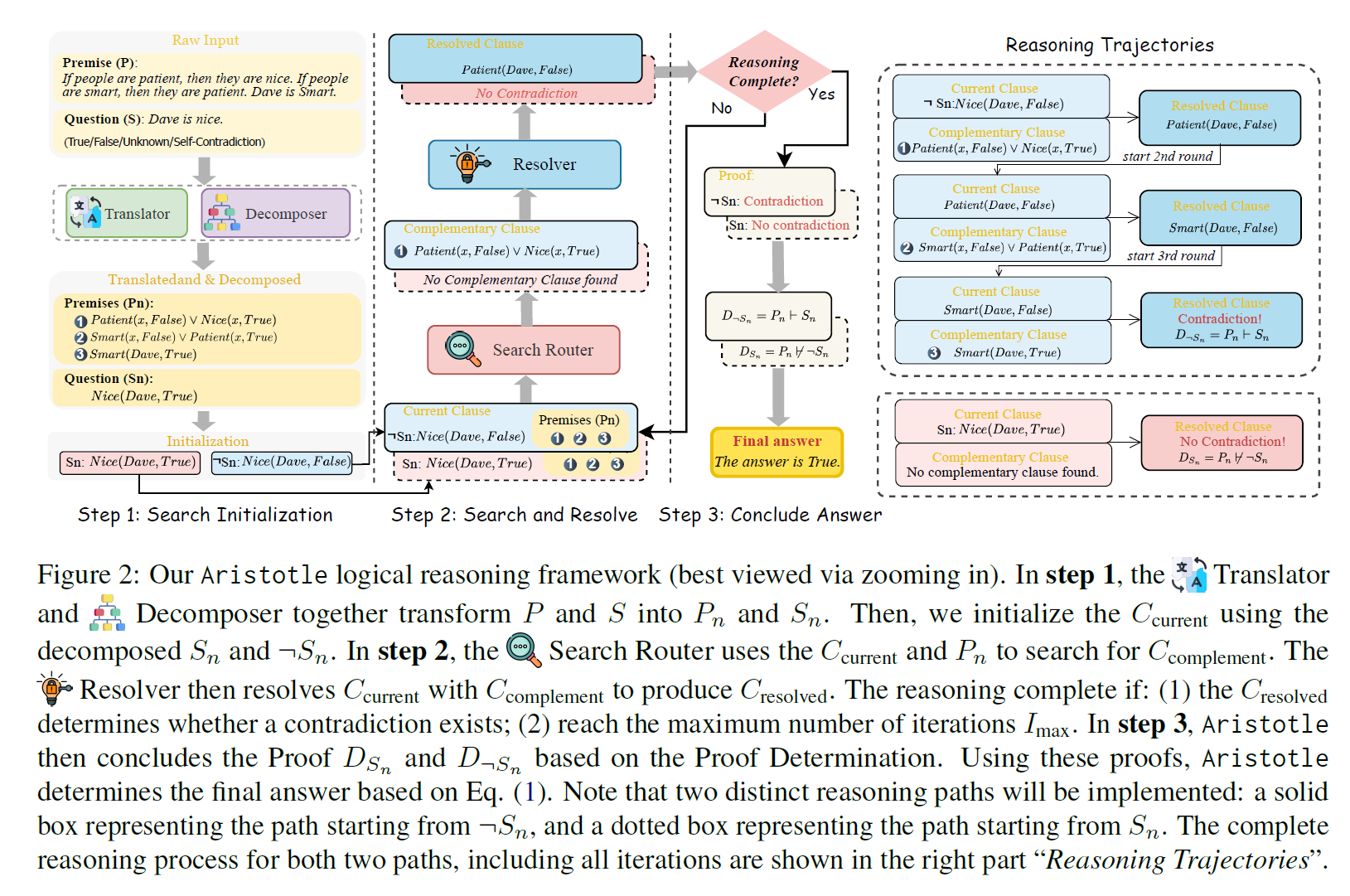
As illustrated in Fig. 2, Aristotle has an architecture with four modules: Translator, Decom-poser, Search Router, and Resolver.
Translator
将自然语言的前提 P 和问题 S,转化为形式化的逻辑符号表示Pt St
We use the LLM itself to parse the given premises P and question statement S into a symbolic format, which aims to eliminate ambi-guity and ensure precision in the logical statement. We specifically use Logic Programming (LP) lan-guage, adopting Prolog’s grammar (Clocksin and Mellish, 2003) to represent the problem as facts, rules, and queries. Facts and rules (Baader et al., 2003) are derived from P , while queries are for-mulated based on the S. We denote the translated premises (facts and rules) as Pt, and queries as St(翻译后的). The details of the grammar can be found at A
Decomposer.
目标:将符号化后的前提 Pt和问题 St,标准化处理成逻辑系统便于操作的形式Pn Sn。
By breaking down the logical statement into a standardized logical form, we can simplify the reasoning process, making it easier to apply formal rules and perform efficient logical calculations.
we use an LLM to transform the parsed premises Pt, and queries St into a standardized logical form through Normalization (Davis and Putnam, 1960) and Skolemization(斯科勒姆化) (Nonnengart, 1996), converting them into Conjunctive Normal Form (CNF) and eliminates quantifiers, denoted as Pn and Sn(规范化后的)
e.g
原始表达式:
∀x (P(x) → Q(x))
第一步:去除蕴含符号
蕴含 A → B 等价于 ¬A ∨ B。所以:
∀x (¬P(x) ∨ Q(x))
第二步:进入Skolemization阶段(如果存在存在量词会替换)
在这个例子中我们只有全称量词 ∀x,我们可以将其视为“对所有 x 成立”,在逻辑证明中可省略或等价于考虑任意一个 x 的情况。因此,最终我们关注的是表达式本体:
¬P(x) ∨ Q(x)
Skolemization
去掉量词(特别是存在量词 ∃),并用函数代替它们。
比如:
-
原始公式: ∀x ∃y Loves(x, y)
-
Skolem 化后: ∀x Loves(x, f(x))
这里 f(x)是一个 Skolem 函数,表示“对每个 x,存在一个具体的人 y=f(x),使得 x 爱 y”。
目的:用函数消除“存在”的不确定性,使公式更便于机器处理。
Search Router
目标:执行逻辑推理的搜索过程,使用**反证法(proof by contradiction)**来发现逻辑冲突。
We adopt the proof-by-contradiction (Bishop, 1967) approach because it allows us to straightforwardly search for complementary clauses. This method reduces search errors and directly targets logical conflicts, making the reasoning process faster and more efficient.
We de-sign a rule-based module to search for the clauses Ccomplement ∈ Pn such that Ccurrent(当前子句) and Ccomplement(互补的子句) contain complementary terms.
互补 complementary 定义:
-
具有相同谓词predicate和参数argument,但极性 polarity相反(正 vs 负)
For example,
if the Ccurrent is P(x, True),
clauses in the premises that contains P(x, False) will be found by the Search Router as Ccomplement, since they are complementary (same predicate P and argument x but opposite polarity (True vs. False)).
Resolver
用于在“反证法”(proof by contradiction)框架下,执行逻辑**合取解析(resolution)**操作,以一步步简化并最终判断逻辑表达式是否成立或矛盾。
To conduct effective step-wise reasoning during proof by contradiction, we adhere to the resolution principle (Robinson, 1965) as it provides clear and concise instructions to resolve logical conflicts, minimizing the likelihood of reasoning errors. Specifically, it works by canceling out the complementary terms identified by the Search Router(对由 Search Router 识别出的互补项进行消除) and connecting the remaining terms(把剩下的项合并起来).
Specifically, given two clauses Ccurrent and Ccomplement, where:
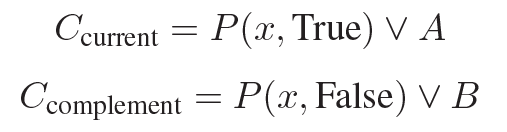
Here, P (x, True) and P (x, False) are complementary terms. The Resolver cancels out them and connects the remaining terms. The resolved clause becomes:

If the remaining clause is empty or contradiction (⊥)^2 , we can conclude the proof and determine the answer, which will be explained in detail in Section 3 at Step 2.
原来的两个子句中,除了 P(x, True) 和 P(x, False) 被删除,其余部分 A 和 B 被连接起来组成一个新的子句。
“P(x, True)” 和 “P(x, False)” 是互补项,它们互相抵消,被认为是**“没有用的信息”**,或者说:
-
它们表达了冲突的事实(一个说为真,一个说为假)
-
所以在 反证推理 中,它们可以被直接消除
然后,保留下来的就是子句中剩余的部分:
Cresolved=A∨B
Logic-Complete Reasoning Processing
Step 1: Search Initialization.
把原始的前提 P 和问题陈述 S 翻译成符号逻辑形式,并准备开始反证。
As shown in the step 1 of Fig. 2, given the original premises P and the question statement S, we first translate them into symbolic format Pt and St, and then decompose them into Pn and Sn, respectively.

To implement proof by contradiction, we initialize the current clause Ccurrent with both Sn and its negation ¬Sn. Considering both Sn and ¬Sn is necessary because we need both proofs to scrupulously conclude an answer(同时从命题 Sn 和它的否定 ¬Sn 开始两个推理路径), which is marked in Eq.(1)
Step 2: Search and Resolve.
通过归结(resolution)不断搜索矛盾,来实现反证。
At this stage, two reasoning paths are initiated: one from Ccurrent = Sn and the other from Ccurrent = ¬Sn, initialized in Step 1. We aim to reach a final answer using proof by contradiction for both paths, iteratively search for complementary clauses and resolve conflicts.
Search
Specifically for each rea-soning path, presented in the Step 2 of Fig. 2, the Search Router selects clauses Ccomplement ∈ Pn that are complementary to Ccurrent. (从 Pn 中找出与当前子句互补(complementary)的子句 C_complement。)

Resolve
The Resolver module then applies the resolution rule Resolve(Ccurrent, Ccomplement) to produce a new clause Cresolved. 将 C_current 和 C_complement 应用归结规则,得出新子句 C_resolved。

If the Cresolved indicates a contradiction or confirms the absence of a contradiction, we then terminate the reasoning process.
If not, we then update Ccurrent = Cresolved and repeat the Search and Resolve process.
If the process reaches the maxi-mum number of iterations Imax and still does not find a contradiction, we conclude that there is no contradiction and terminate the reasoning process. Given the determination of whether contradiction exists, we then use the formula presented below to formally establish the proof DSn (started from Ccurrent = Sn) and D¬Sn (started from Ccurrent = ¬Sn) to determine whether Pn entails either Sn or ¬Sn.

Step 3: Conclude Answer.
根据两个推理路径是否找到矛盾,得出陈述 S 的真假
This proof DSn and D¬Sn can then be used to conclude the truth value A of S based on Eq. (1). For example, consider a statement S. If we get DSn = P ⊢ ¬S and D¬Sn = P ̸⊢ S, the combination of P ⊢ ¬S and P ̸⊢ S leads to the conclusion A that S is false according to Eq. (1).
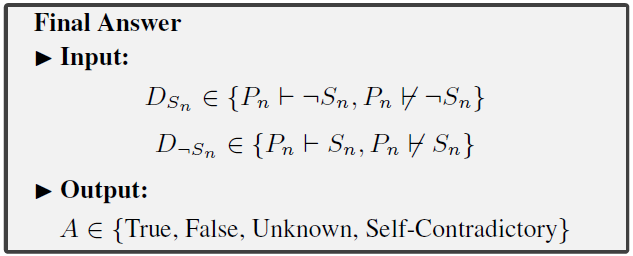
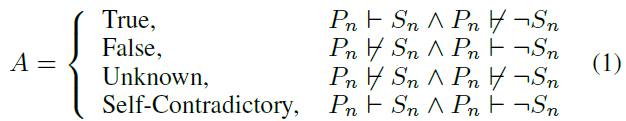
The full algorithm and an example case can be found in Appendix G and H, respectively.
Experiments
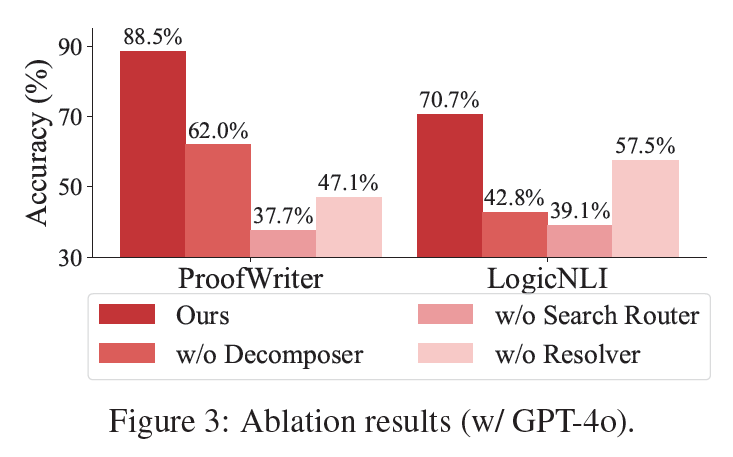
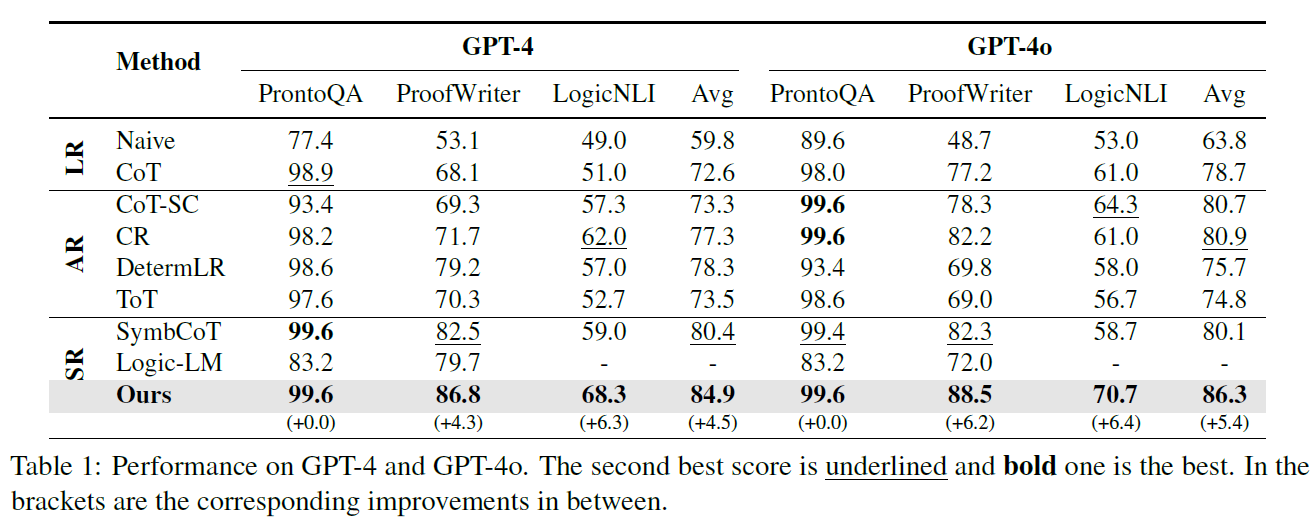






















 518
518

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








