吴恩达深度学习1笔记week3——浅层神经网络 One hidden layer Neural Network

最新推荐文章于 2023-01-29 11:33:55 发布
原创 最新推荐文章于 2023-01-29 11:33:55 发布 · 432 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#深度学习

本文为吴恩达深度学习课程第三周的学习笔记，主要介绍浅层神经网络的基本概念，包括神经网络的表示、计算输出的方法、向量化实现及激活函数的选择等。此外还探讨了非线性激活函数的重要性及其导数计算，并介绍了神经网络中的梯度下降法。

吴恩达深度学习笔记week3——浅层神经网络 One hidden layer Neural Network

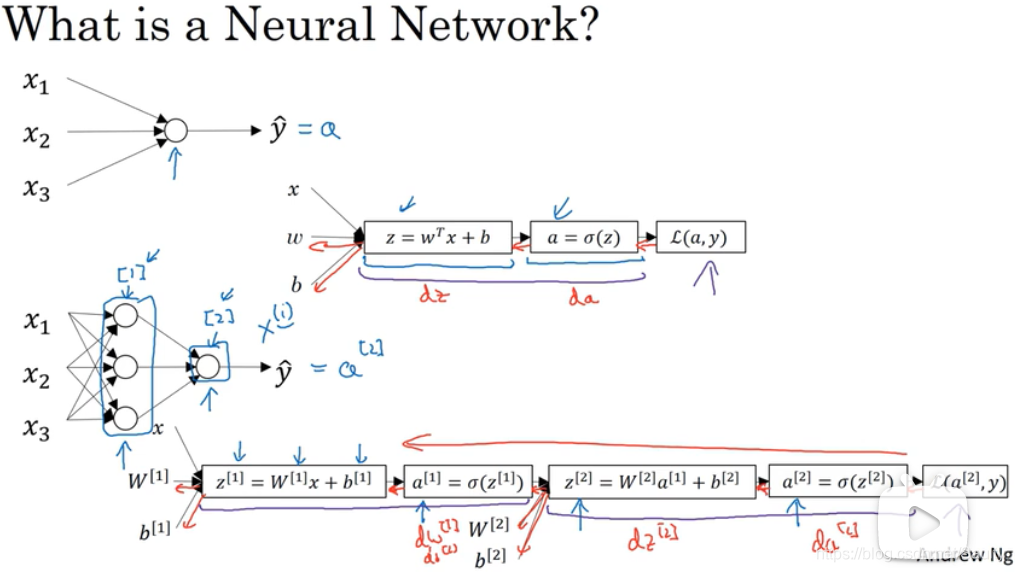
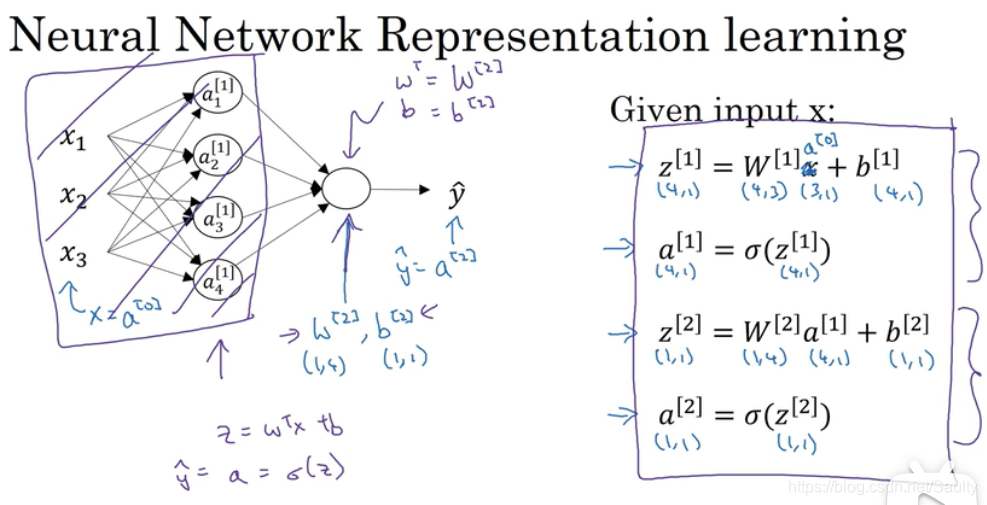
3.1 神经网络概览 Neural Networks Overview在这里插入图片描述

3.2 神经网络表示 Neural Network Representation

  • 当我们计算网络层数的时候，一般不算上输入层
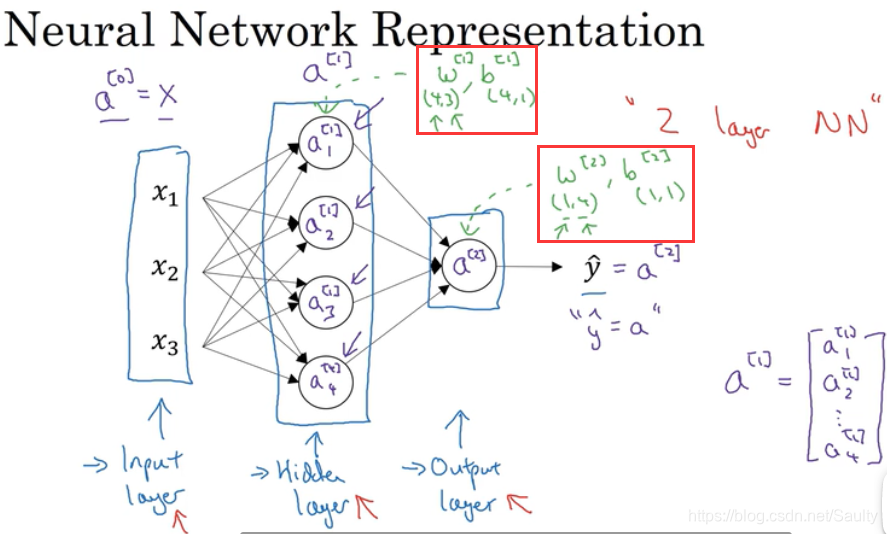
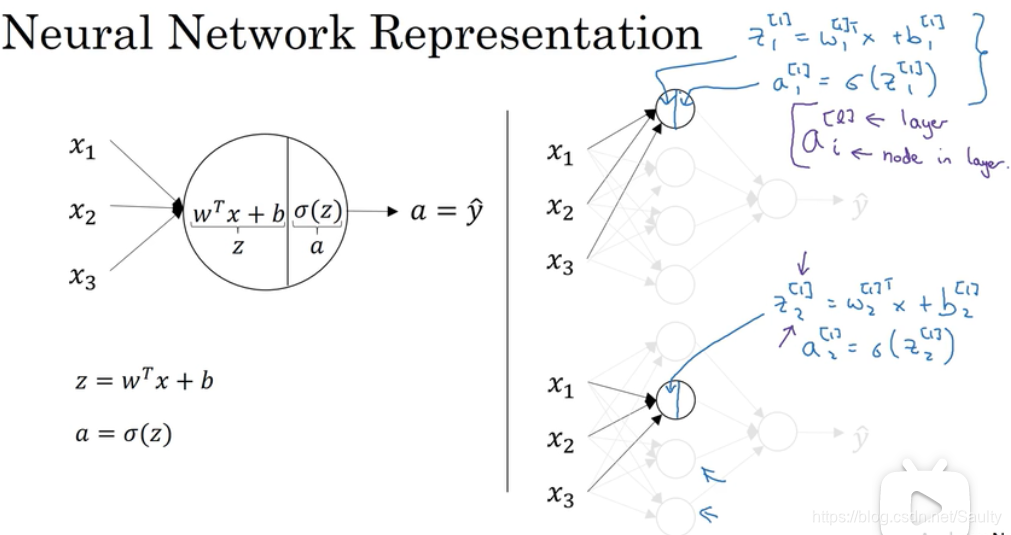
    在这里插入图片描述

3.3 计算神经网络的输出 Computing a Neural Network’s Output

  • 两步走
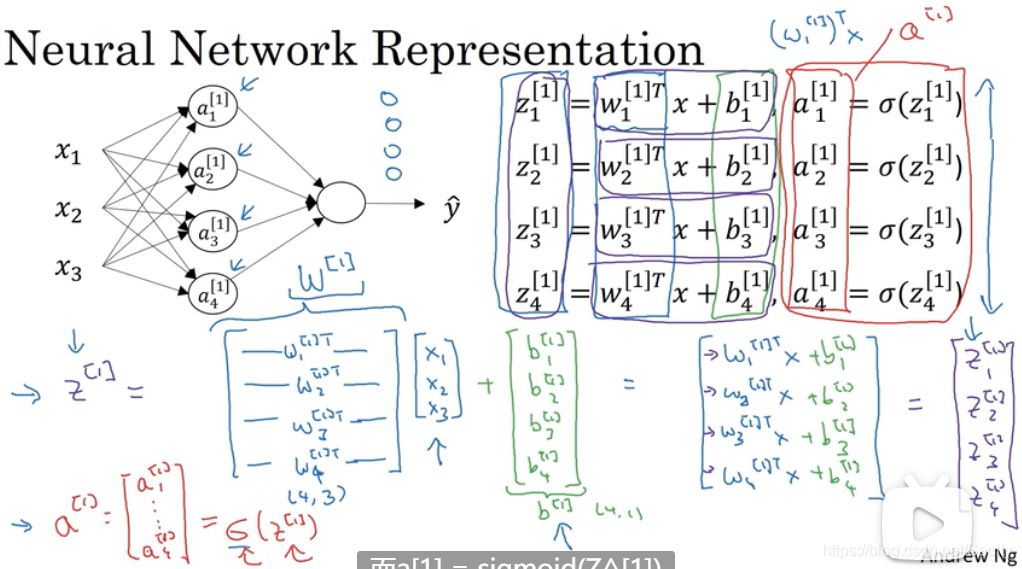
    在这里插入图片描述
  • 向量化
    在这里插入图片描述
    在这里插入图片描述

3.4 多个例子中的向量化 Vectorizing across multiple examples

  • 注意上标 [ ] 和 （）
    （）代表第几个样本
    [ ] 代表第几层
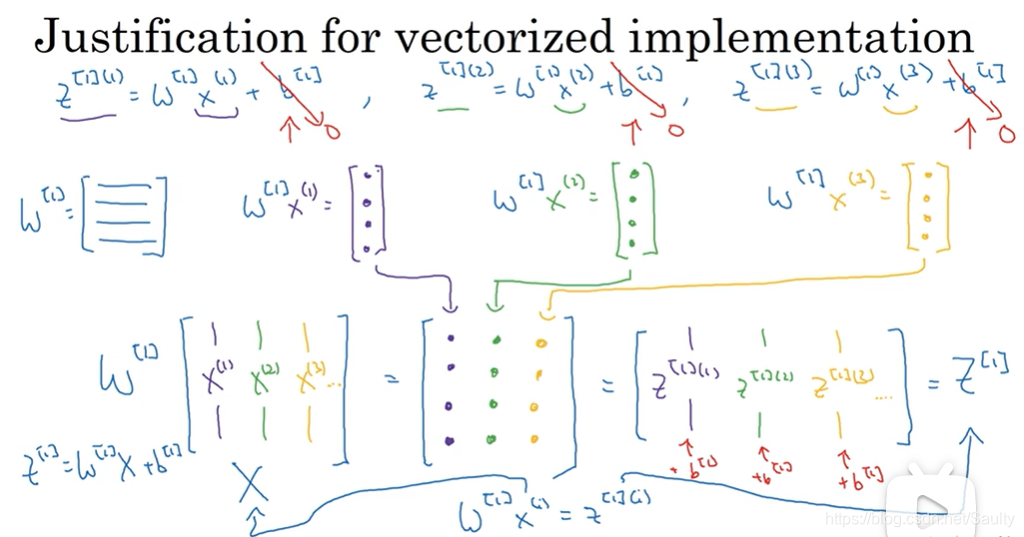
    在这里插入图片描述
    在这里插入图片描述

3.5 向量化实现的解释 Explanation for vectorized implementation

  • 不同的样本在每一层的参数是相同的
  • 同一样本不同特征在每一层的参数是不同的
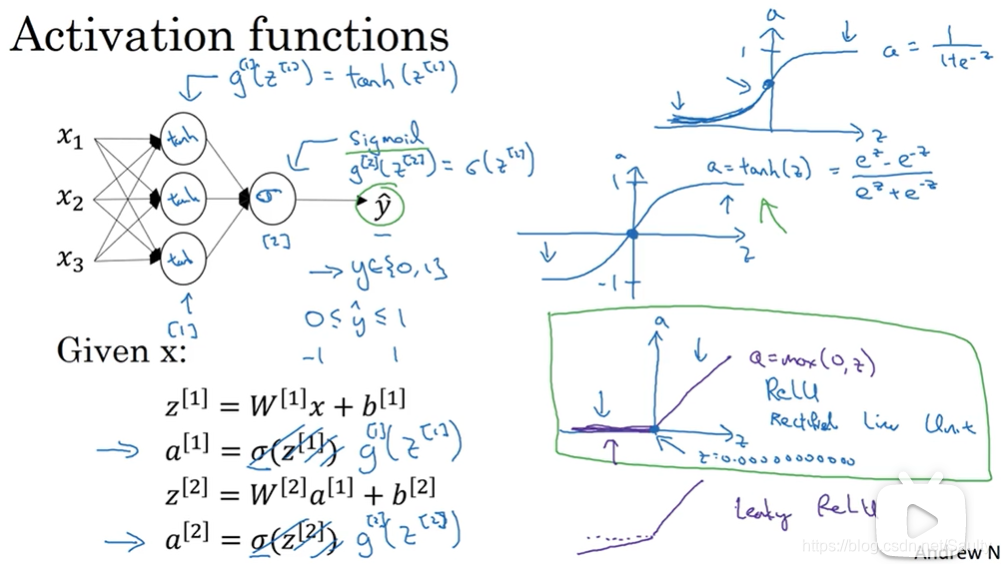
    在这里插入图片描述
    在这里插入图片描述

3.6 激活函数 Activation functions

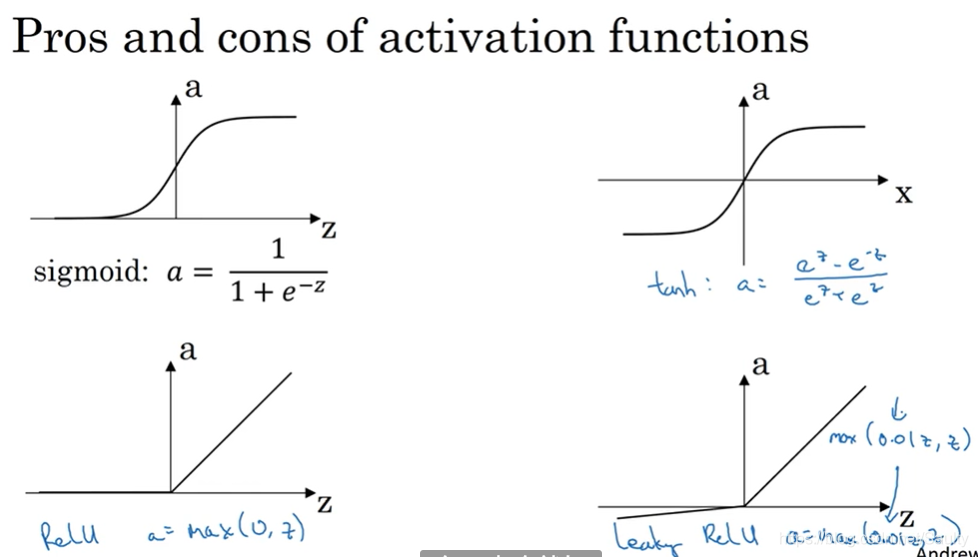
在这里插入图片描述
在这里插入图片描述

3.7 为什么需要非线性激活函数？Why do you need non-linear activation functions?

  • 为了提高模型的复杂度
  • 线性函数组合本身就是线性函数
  • 若只使用线性激活函数，与不使用隐藏层的逻辑回归函数无异
    在这里插入图片描述

3.8 激活函数的导数 Derivatives of activation functions

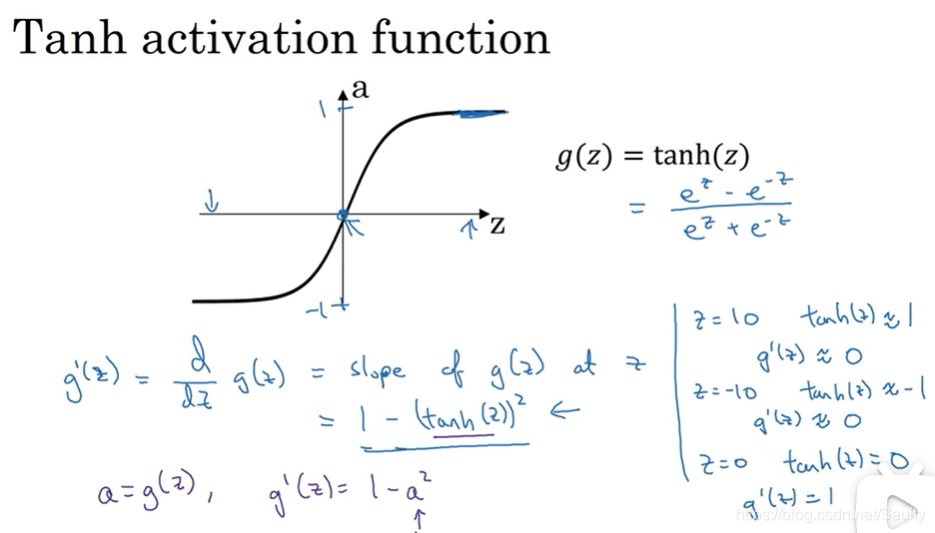
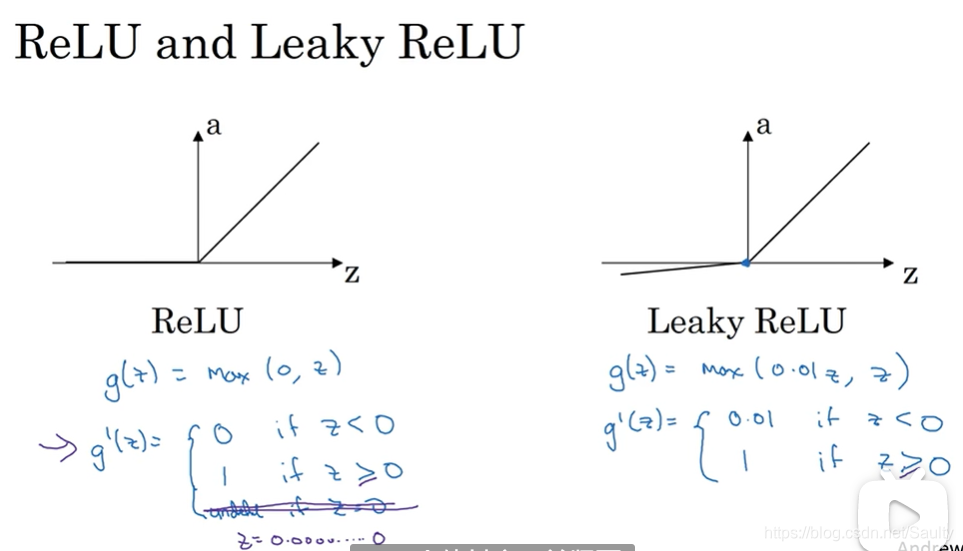
在这里插入图片描述
在这里插入图片描述

3.9 神经网络的梯度下降法 Gradient descent for neural networks

在这里插入图片描述
在这里插入图片描述

3.10 （选修）直观理解反向传播 Backpropagation intuition

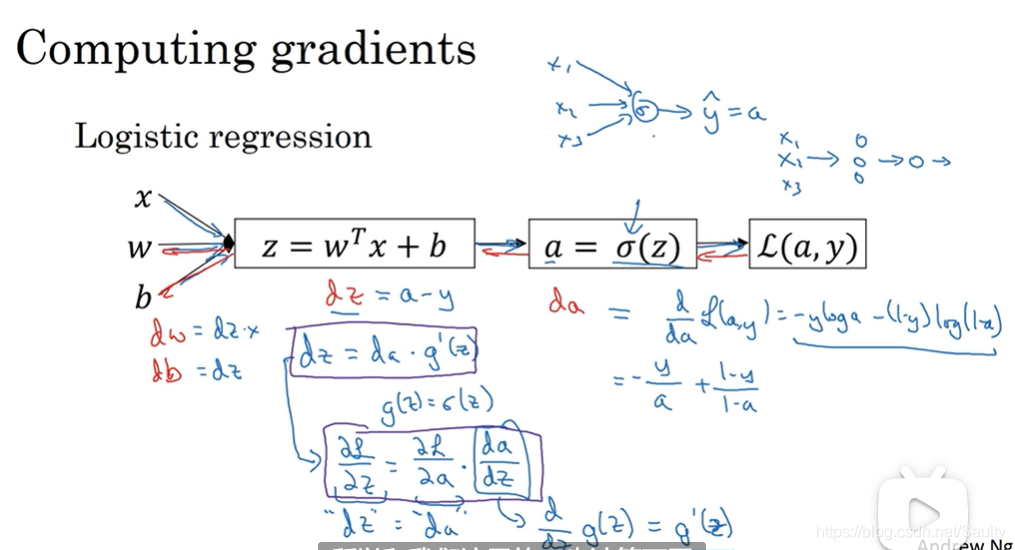
在这里插入图片描述

  • 单个样本
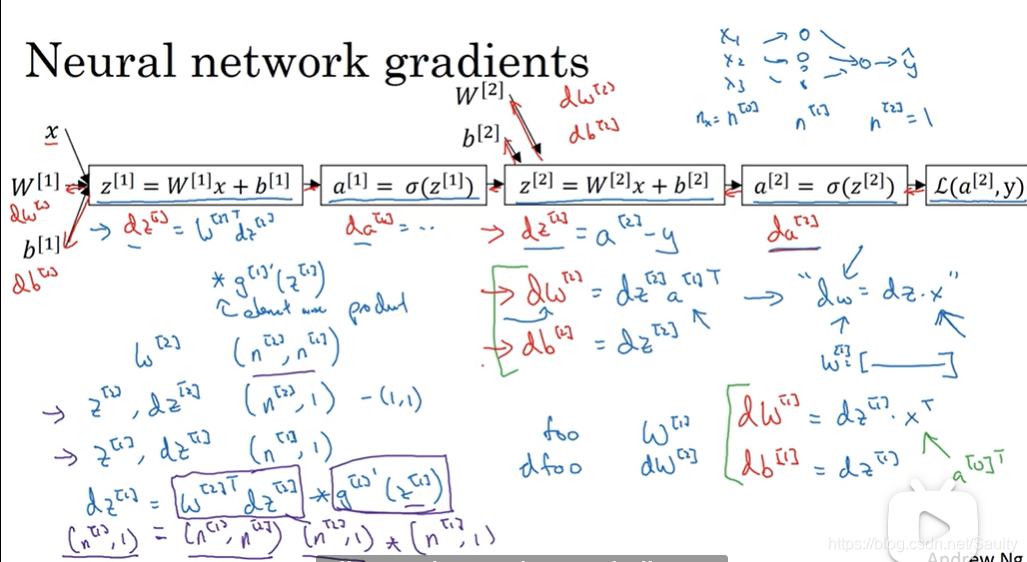
    在这里插入图片描述
  • 多个样本
    前向传播
    在这里插入图片描述
    反向传播
    在这里插入图片描述

3.11 随机初始化权重 Random Initialization

  • 对称性问题
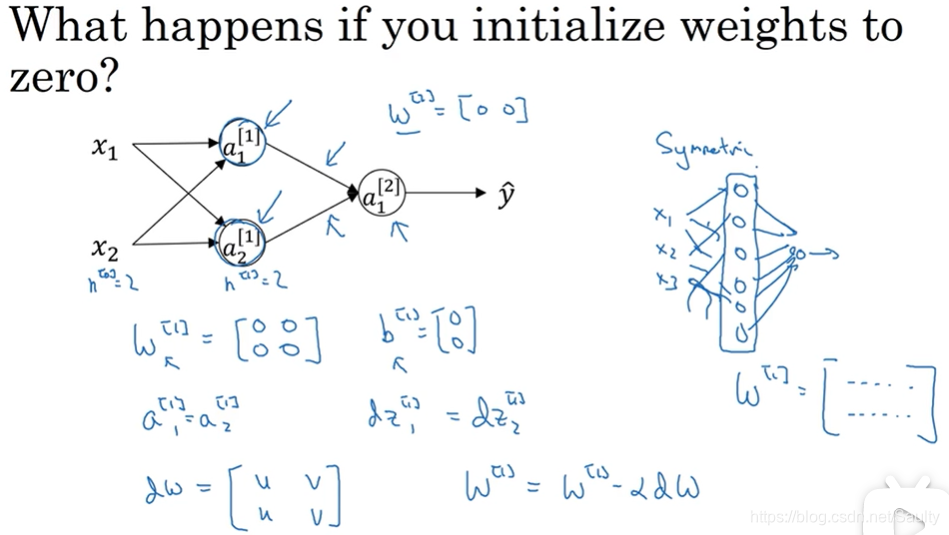
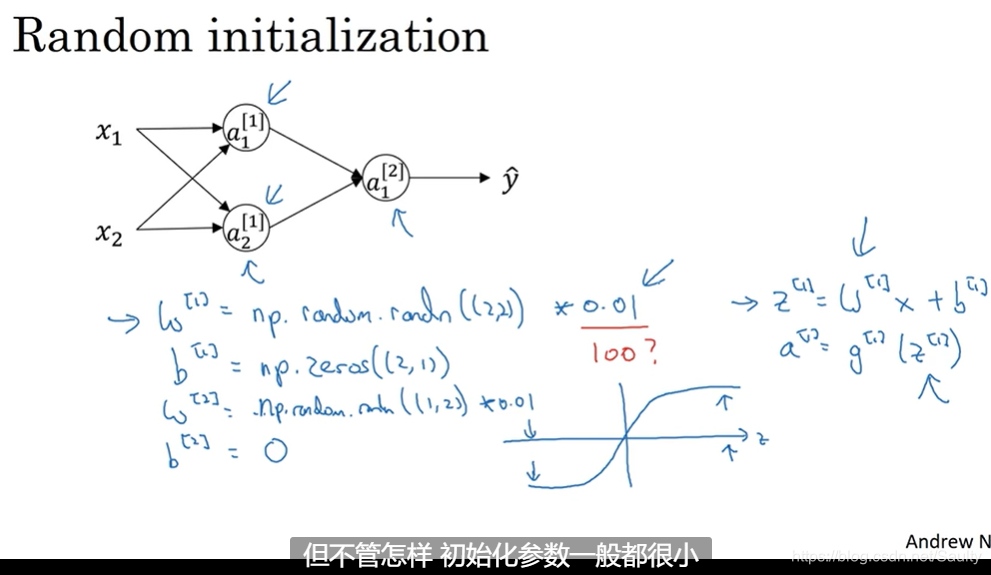
    在这里插入图片描述
    在这里插入图片描述
Saulty
关注
浅层神经网络（One Hidden Layer Neural Network）
qq_32865355的博客
12-27 6225
在之前课程中，我们实现了逻辑回归函数，它是一个不包含隐藏层的网络结构。 本节课中，我们将继续神经网络的学习，本文主要来讲解包含一个隐藏层的神经网络结构及其原理。 本文内容概述 之前的文章中，我们讲述了一个逻辑回归的模型如下： 其中，输入参数包含w, x和b，具体计算流程如下： 而对应一个包含隐藏的神经网络而言，其网络结构如下：
Course1-week3-one hidden layer neural network
XuShuai
06-08 646
3.1 - neural networks overview Some new notation have been introduce, we’ll use superscript square bracket 1 to refer to the layer of neural network, for instance, w[1]w[1]w^{[1]} representing the pa...
One hidden layer Neural Network - Neural Network Representation
王彩旗的技术博客
07-05 176
The notes when study the Coursera class by Mr. Andrew Ng "Neural Networks & Deep Learning", section 3.2 "Neural Network Representation". Share it with you and hope it helps! ------------------ figure-1 Figure-1 shows names of different parts of Neura
吴恩达深度学习作业/01.机器学习和神经网络/3.第三周浅层神经网络/编程作业/Planar data classification with one hidden layer
我不是程序员的博客
07-30 619
Planar data classification with one hidden layer Welcome to your week 3 programming assignment. It’s time to build your first neural network, which will have a hidden layer. You will see a big difference between this model and the one you implemented using
神经网络与深度学习第三周-Planar data classification with one hidden layer
Suika_Neko的博客
11-18 2514
Planar data classification with one hidden layer(用一个隐藏层平面数据分类) Welcome to your week 3 programming assignment. It’s time to build your first neural network, which will have a hidden layer. You will se...
吴恩达 深度学习 编程作业（5-1）Part 1 - Building your Recurrent Neural Network
大树先生的博客
03-05 1万+
一步步建立一个RNN：Building your Recurrent Neural Network - Step by Step
吴恩达 深度学习 编程作业（1-4）- Building your DNN & DNN for Image Classification: Application
热门推荐
大树先生的博客
09-26 3万+
Part 1：Building your Deep Neural Network: Step by Step Part 2：Deep Neural Network for Image Classification: Application
吴恩达 深度学习 编程作业（5-3）Part 1 - Neural Machine Translation
大树先生的博客
04-04 5828
机器翻译 —— Neural Machine Translation：日期转换、注意力权重可视化
吴恩达 深度学习1 2022， 浙大AI第一课
linyuxi_loretta的博客
10-11 483
举个算法改进的例子，NN一个巨大的突破是，之前神经网络神经元的激活函数是Sigmoid函数，后来改成了ReLU函数。gradient=0，参数会变化的很慢，学习也会变的很慢）。然而，ReLU函数在x大于零的区域，其梯度始终为1，尽管在x小于零的区域梯度为0，但是在实际应用中采用ReLU函数确实要比Sigmoid函数快很多。神经网络在很多短期经济价值的创造，是基于Structured Data，e.g.广告系统，better profit recommendations，处理很多公司拥有的海量数据库，
Machine Learning - Coursera 吴恩达机器学习教程 Week4 学习笔记
zhang35的博客
02-04 1393
背景 当目标函数非线性时（比如下图明显需要一条曲线），就需要增加高次项来获得曲线，当特征数量比较多时，增加高次项会使特征数量爆炸式增长。 比如图像识别问题，对50 * 50像素的图像，如果将每个像素作为特征，增加二次特征就会产生约3 * 10 ^ 6个特征（C22500 = 2500 * 2499 / 2） 这种情况下，若要使用普通逻辑回归学习所有特征，计算量就过大了。 此时用神经网络学习这种复杂的非线性假设函数，就比较合适了。 神经网络 首先学习几个术语： dendrite: 树突（输入） cell
吴恩达 Planar+data+classification+with+one+hidden+layer+v4.ipynb
01-21
吴恩达 planar data classification with one hidden layer 答案
Python:实现 hidden layers neural network浅层神经网络算法(附完整源码)
希望我的博客，能帮上你解决学习中工作中所遇到的问题
08-02 484
Python:实现 hidden layers neural network浅层神经网络算法(附完整源码)
One hidden layer Neural Network - Random Initialization
王彩旗的技术博客
07-12 139
When you train your NN, it's important to initialize the weights ( etc.) randomly. For logistic regression, it's ok to initialize the weights to 0; but for NN, if initialize the weights all to 0 and then apply gradient descent, it won't work!
deepLearning-One hidden layer Neural Network一个隐藏层的神经网络
OneForPlus的博客
01-06 427
一个隐藏层的神经网络的个人总结
【Course 1 神经网络与深度学习】Week 3 浅层神经网络
FREEDOM’s blog
08-13 613
One hidden layer Neural Network 1.Neural Network Overview and Representation 从整体结构上来大致看一下神经网络模型，神经网络的结构与逻辑回归类似，只是神经网络的层数比逻辑回归多一层，多出来的中间那层称为隐藏层或中间层。==隐藏层是抽象的非线性的中间层。==这样从计算上来说，神经网络的正向传播和反向传播过程只是比逻辑回归多了一次重复的计算。 正向传播过程分成两层，第一层是输入层到隐藏层，用上标[1]来表示；第二层是隐藏层到输出层，用上
深度学习 deep neuron network（DNN）hidden layer and how it works
weixin_42666153的博客
01-02 267
hidden layer and how it works 【【官方双语】深度学习之神经网络的结构 Part 1 ver 2.0-哔哩哔哩】 【什么是深度神经网络DNN-哔哩哔哩】
3.深度学习练习：Planar data classification with one hidden layer
10点43的博客
06-28 685
本文节选自吴恩达老师《深度学习专项课程》编程作业，在此表示感谢。 课程链接：https://www.deeplearning.ai/deep-learning-specialization/ You will learn to: Implement a 2-class classification neural network with a single hidden layer Use...
吴恩达深度学习与神经网络编程作业——planar data classification with one hidden layer
qq_38938670的博客
09-08 576
记：该编程作业是第三周的作业，第二周我们完成了一个Logistic regression模型，改模型没有隐藏层，今天要完成的是有一个隐藏层的分类神经网络（即2层神经网络），同时会对比二者的不同之处（即适用情况）。（很多是根据个人理解的情况写的，如有错误还望指出） 1、实验中用到的包 # Package imports import numpy as np import matplotlib.pyplot as plt from testCases import * import sklearn imp
Coursera深度学习：Planar data classification with one hidden layer
elfighting的博客
01-29 255
Coursera深度学习 Planar data classification with one hidden layer神经网络代码实现
深度学习笔记：吴恩达第三周浅层神经网络解析
“第三周：浅层神经网络.pdf，吴恩达深度学习与神经网络课程笔记，涵盖了神经网络的基础知识，包括概述、表示、输出计算、向量化、激活函数、非线性需求、导数、梯度下降以及随机初始化。” 在这一周的学习中，我们...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值