吴恩达机器学习笔记week3——线性代数知识点回顾

3-1.矩阵(Matrix)和向量(Vector)

矩阵与向量：
矩阵的维数：mn（行数列数）、矩阵中的元素：Aij（i行j列）、向量是一个n1维的矩阵、向量中的元素：yi表示第i个元素。
通常用大写字母表示矩阵，小写字母表示向量。
一般情况下，矩阵和向量的下标索引值从数字1开始。
R表示实数集，Rmn表示m*n维矩阵，矩阵中元素为实数。

3-2.加法和标量乘法

只有两个相同维度的矩阵才可以进行加减法。

3-3.矩阵向量乘法

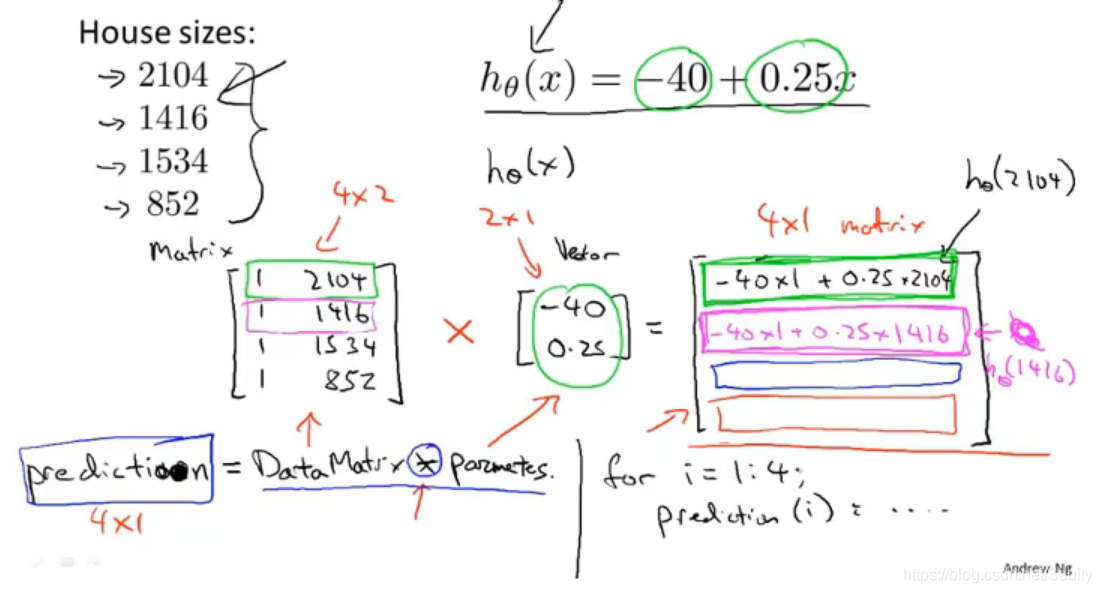
3-4.矩阵乘法

矩阵乘法不满足交换律AB!=BA，但是满足结合律ABC=A*(B*C)

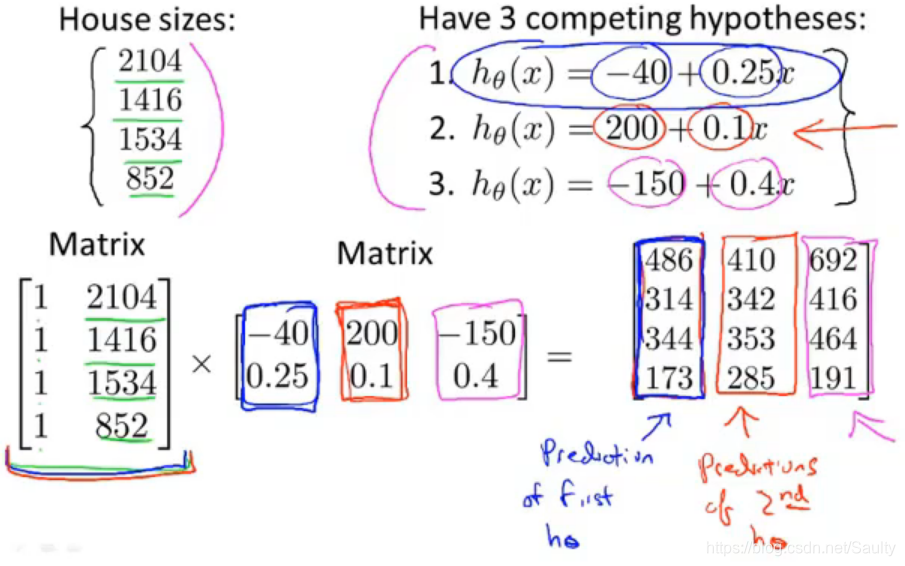
一列一列对应着看

3-5.矩阵乘法特征

I为单位矩阵，AI=IA=A.

3-6.逆和转置

矩阵的逆(Matrix Inverse)：AA-1=A-1A=I，其中A为mm维的方阵，只有方阵才有逆矩阵。
矩阵的转置(Matrix Transpose)：Amn，B=AT，Bn*m，and Bij=Aij