数字图像分割（三）：相似性分割——区域生长与K均值聚类

在灰度的阈值分割部分，就已经提到了类似于K-means的分割思想。

但本次的相似性分割与灰度值中的相似性分割有一个最大的区别：本次的像素要求连通！

这直接让分割任务上了一个档次，对于灰度值的自适应阈值来讲，只需统计图像中的灰度值分布情况与分类就行，不需要考虑像素点是否连通。

但是对于区域生长方法来讲，像素点连通则是区域生长算法的前提！

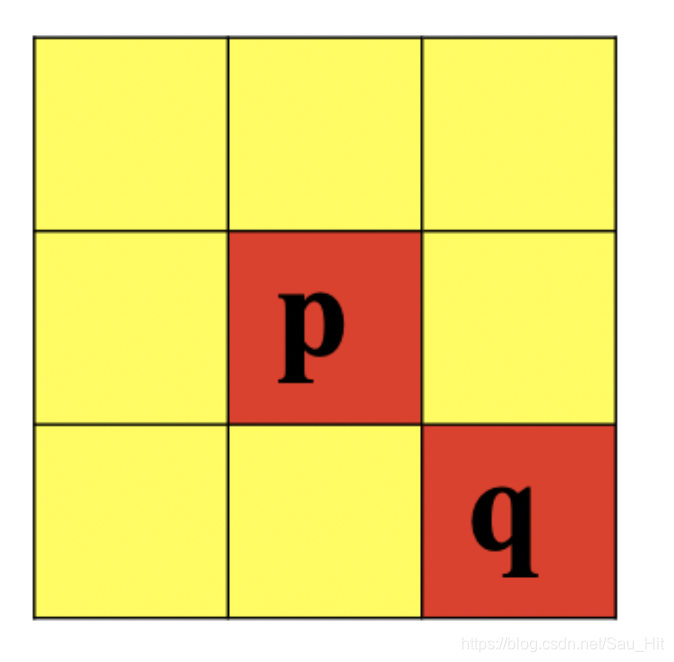
四邻域：

（这里坐标只是示意：具体是Opencv坐标还是图像处理坐标，还是笛卡尔坐标视实际情况！）

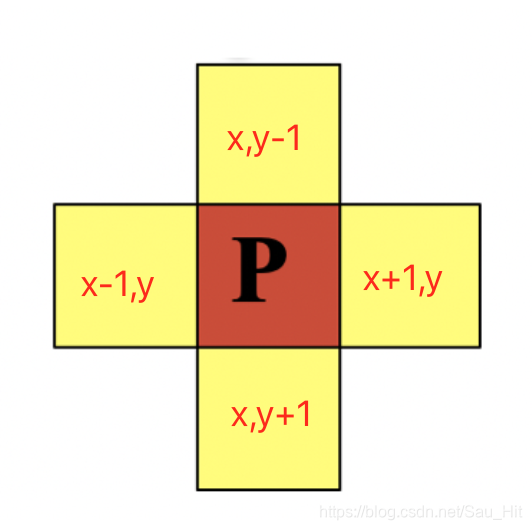
D邻域：

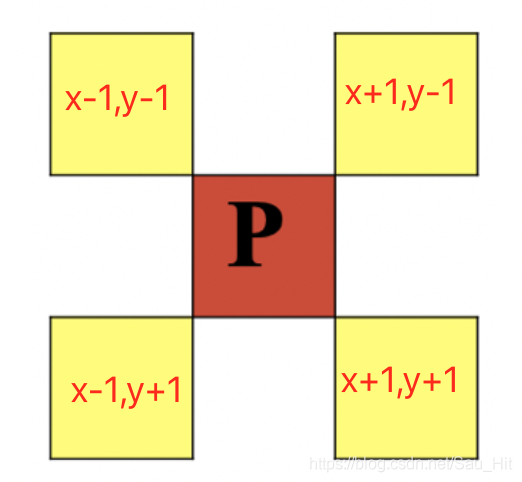
8邻域：

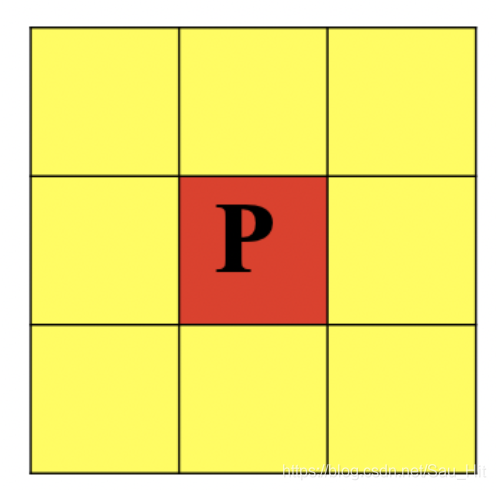
邻域有了，接下来就是连通，关于连通方面，还是需要好好去理解的，

毕竟连通性对于今后的区域图像分割起到了一定的限制作用!

在邻域内满足相似性条件，就成为连通。

对应的有4连通，8连通，以及m连通。

4连通：

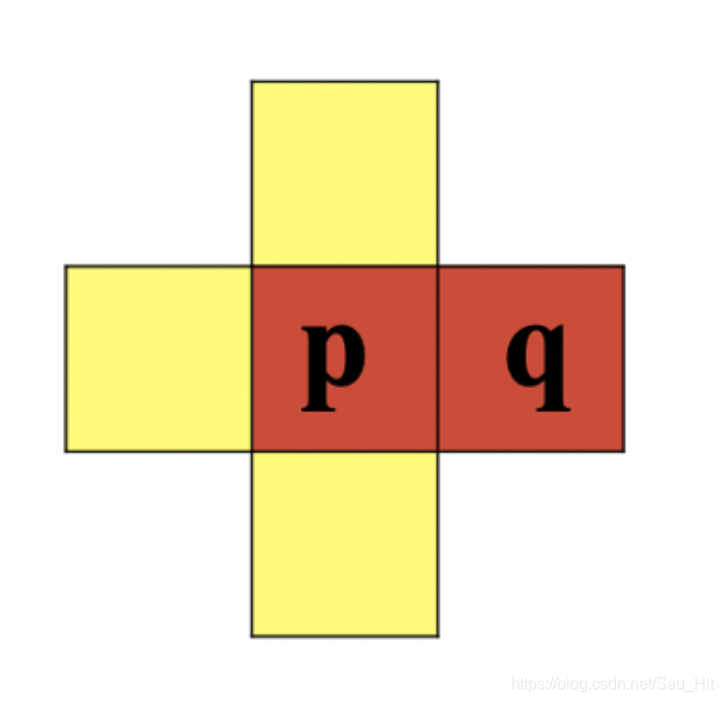
8连通：

关于m连通，理解有点绕：整体上就是4连通+D连通，但是，二者4连通上没有交集。

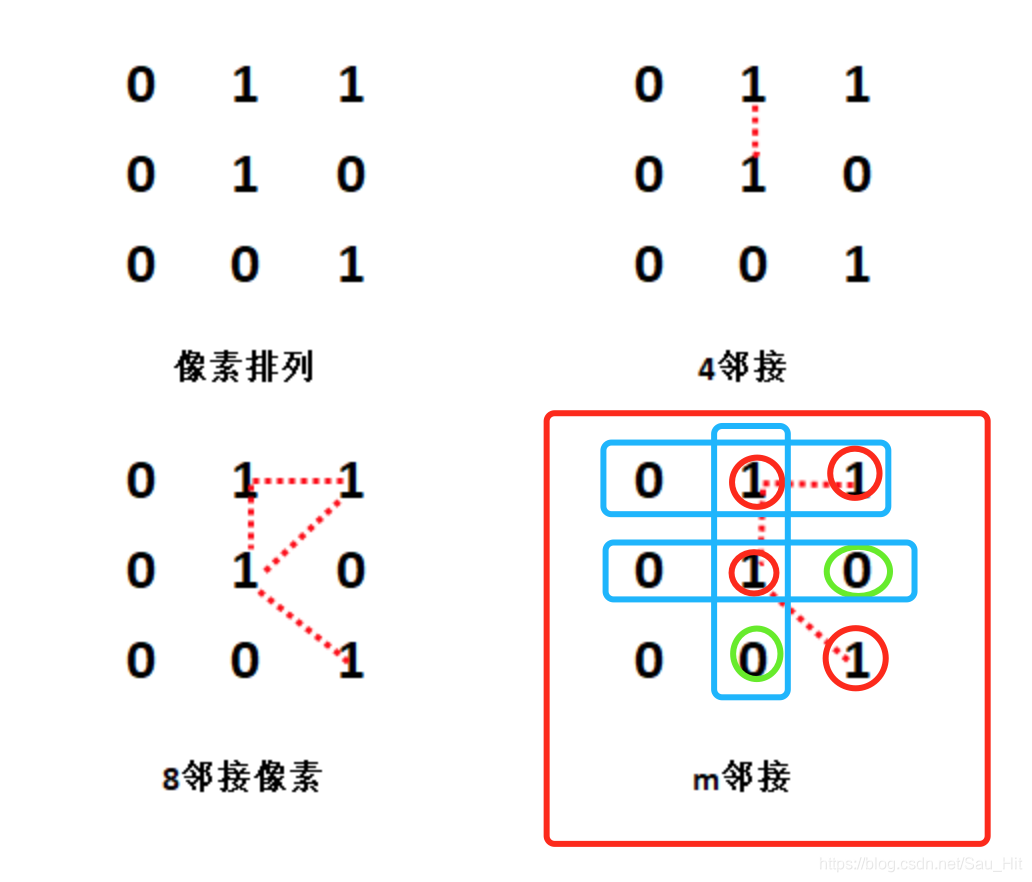
文字不容易表达出来，今后有例子再添加。

我们如何用代码来实现，判断是否连通呢？（以四连通为例）

判断连通是关键，但是该怎么做呢？

1.逐点判断，可能会存在重复值

2.将连通域寻找到底

这里纠正一下，不是去判断是否连通，在实际的代码中是根据连通去操作像素点！！！

不是判断，而是利用连通性去实现算法

use it , not prove it

# 此处的代码先遗留，等将图割部分共同完成后，回来补上代码。

 

写到这里，发现逻辑原理十分简单，但代码方面，该找一个怎样合适的算法是一个技术活。

这里的区域生长算法，与K均值聚类，都可用到树的存储结构来存储连通pixel

这里的差值计算也与图割也有交集。

具体怎么做，还要参考Github上的大神，关于图割与区域生长的具体做法。

未完成，后续更改。

# 后续仍要添加代码
# 2020-09-26