动态规划入门#矩阵连乘问题

动态规划算法通常用来求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。

动态规划算法与分治法类似，其基本思想也是将待求解的问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
与分治法不同的是，适用于用动态规划求解的问题，经分解得到的子问题往往不是互相独立的。若用分治法来求解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。
可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。

以上就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。

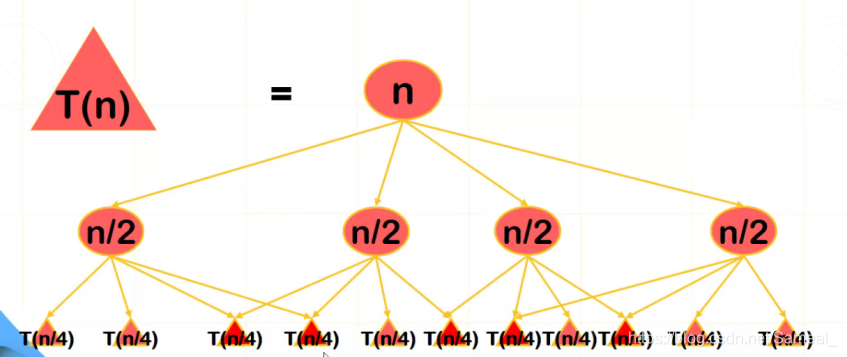
（保存子问题的答案，从而避免重复计算）

基本步骤

1.找出最优解的性质，并刻画其结构特征。
2.递归地定义最优值（写出动态规划方程）。
3.以自底向上的方式计算出最优值。
4.根据计算最优值时得到的信息，构造最优解。

步骤1-3是动态规划算法的基本步骤。在只需要求出最优值的情形，步骤4可以省略，步骤3中记录的信息也较少；若需要求出问题的一个最优解，则必须执行步骤4，步骤3中记录的信息必须足够多以便构造最优解。

动态规划问题的特征
动态规划算法的有效性依赖于问题本身所具有的两个重要性质：最优子结构性质和子问题重叠性质。
最优子结构性质：当问题的最优解包含其子问题的最优解时，称该问题具有最优子结构性质。
重叠子问题：在用递归算法自顶向下解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算了多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只解一次，而后将其解保存在一个表格中，在以后尽可能多地利用这些子问题的解。

示例问题
一、矩阵连乘问题
给定n个矩阵{A1，A2，…，An}，其中Ai与Ai+1是可乘的，i=1,2，…，n-1。考察这n个矩阵的连乘积：
A1A2…An

矩阵连乘具有许多计算顺序，这种计算顺序可以用加括号的方式来确定。
如果一个矩阵连乘积的计算顺序完全确定，也就是说该连乘积已完全加括号；则可以依此次序反复调用两个矩阵相乘的标准算法计算出矩阵连乘积。

#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=50;

//p[]表示矩阵维数   m[][]表示相乘次数   s[][]记录断开的位置 
void matrixchain(int p[],int n,int m[maxn][maxn],int s[maxn][maxn]){
	for(int i=1;i<=n;i++)//只有一个矩阵时，相乘次数为0 
		m[i][i]=0;
	for(int r=2;r<=n;r++){//r表示此时有多少个矩阵相乘 
		for(int i=1;i<=n-r+1;i++){
			int j=i+r-1;//j表示相乘的最后一个矩阵 
			m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];//给m[][]初始一个值 
			s[i][j]=i;//同样给s[][]一个初始值 
			for(int k=i+1;k<j;k++){//当相乘的矩阵个数大于二时，矩阵之间相乘的次序有多种 
				int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
				if(t<m[i][j]){//找到所有次序中最小的那个 
					m[i][j]=t;
					s[i][j]=k;//更新两个数组的值 
				}
			}
		}
	}
} 

void traceback(int i,int j,int s[maxn][maxn]){
	if(i==j)return;
	traceback(i,s[i][j],s);
	traceback(s[i][j]+1,j,s);
	cout<<"Multyply A "<<i<<","<<s[i][j];
	cout<<"and A "<<(s[i][j]+1)<<","<<j<<endl;
}

int main(){
	int p[]={30,35,15,5,10,20,25};
	int s[maxn][maxn],m[maxn][maxn];
	int n=6;
	matrixchain(p,n,m,s);
	traceback(1,6,s);
}