Dijkstra算法算是贪心思想实现的,首先把起点到所有点的距离存下来找个最短的,然后松弛一次再找出最短的,所谓的松弛操作就是,遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近,如果更近了就更新距离,这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。
(1) 初始化:
● 将源点v0加到S中,即S[v0]=true
● 将v0到各个终点的最短路径长度初始化为权值,即Dist[i]=G.arcs[v0][vi]
● 如果v0和顶点vi之间有弧,则将vi的前驱置为v0,即Path[i]=v0,否则Path[i]=-1
(2) 循环n-1次执行以下操作:
● 选择下一条最短路径的终点vk,使得Dist[k]=Min{Dist[i]|vi∈V-S}
● 将vk加入到S中,即S[vk]=true
● 根据条件更新从v0出发到集合V-S上任一顶点的最短路径的长度,若条件Dist[k]+G.arcs[k][i]<Dist[i]成立,则更新Dist[i]=Dist[k]+G.arcs[k][i],同时更改vi的前驱为vk;Path[i]=k
算法思想

//图的定义-邻接矩阵
#define MaxInt 32767 //表示极大值 即无穷大
#define MVNum 100 //最大顶点数
typedef string VerTexType; //设顶点的数据类型为string,需#include<string>
typedef int ArcType; //设权值类型为整型
typedef struct
{
VerTexType vexs[MVNum]; //顶点表
ArcType arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //图的当前点数和边数
}AMGraph;
int Dist[MVNum];//Dist存当前找到的最短路径长度
int Path[MVNum];//当前找到的最短路径最后一个中转顶点,也就是想要到达这个点,需要经过哪一个点
bool S[MVNum];//标记当前是否已求出最短路径,也可以理解为true是集合s,false是集合v-s
void ShortestPath_DIJ(AMGraph G, int v0)//求有向网G的v0顶点到其余顶点的最短路径
{
int n, v, i, w, min;
n = G.vexnum;//顶点数
//初始化
for (v = 0; v < n; v++) //n个顶点依次初始化
{
S[v] = false;//S初始为空集
Dist[v] = G.arcs[v0][v];//将v0到各个终点的最短路径长度初始化为弧上的权值
if (Dist[v] < MaxInt) Path[v] = v0;//如果v0与v之间有弧,则将v的前驱置为v0
else Path[v] = -1;//无弧,置为-1
}
//S集合
S[v0] = true;//将v0加入S
Dist[v0] = 0;//原点到原点的距离为0
//******初始化结束,开始主循环,每次求得v0到某个顶点v的最短路径,将v加入到S集
for (i = 1; i < n; i++)//n-1个顶点
{
min = MaxInt;
//找最小的那条路径,并入集合S
for (w = 0; w < n; w++)
if (!S[w] && Dist[w] < min)//选择一条当前的最短路径,终点为v
{
v = w; min = Dist[w];
}
//并入s
S[v] = true;//将v加入S
for (w = 0; w < n; ++w)//更新从v0出发到集合V-S上所有的最短路径长度
if (!S[w] && (Dist[v] + G.arcs[v][w]) < Dist[w])
{
Dist[w] = Dist[v] + G.arcs[v][w];//更新D[w]
Path[w] = v;//更改w的前驱为v
}
}
}打印出从begin到end的路径:
void DisplayPath(AMGraph G, int begin, int temp)
{
if(begin == temp) {
cout << G.vexs[temp] ;
return ;
};
if (Path[temp] != -1)
{
DisplayPath(name, begin, Path[temp]);
cout << "-->"<< G.vexs[temp] ;
}
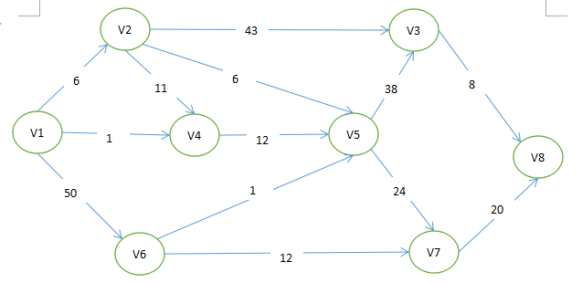
}对于上面的图片经计算v1到v8的最短路径,代码如下:
#include<iostream>
using namespace std;
#define MaxInt 32767 //表示极大值
int Dist[8];//最短路径长度
int Path[8];//中转顶点
bool S[8];//访问标志位
//采用迪杰斯特拉算法,求有向网G的v0顶点到其余顶点的最短路径
void ShortestPath_DIJ(int G[][8], int v0,int nums)
{
int n, v, i, w, min;
n = nums;//顶点数
for (v = 0; v < n; v++) //n个顶点依次初始化
{
S[v] = false;
Dist[v] = G[v0][v];//将v0到各个终点的最短路径长度初始化为弧上的权值
if (Dist[v] < MaxInt) Path[v] = v0;//v0与v之间有弧,则将v的前驱置为v0
else Path[v] = -1;//无弧,置为-1
}
S[v0] = true;
Dist[v0] = 0;
for (i = 1; i < n; i++)//n-1个顶点
{
min = MaxInt;
for (w = 0; w < n; w++)
if (!S[w] && Dist[w] < min)
{
v = w; min = Dist[w];
}
S[v] = true;
for (w = 0; w < n; ++w)
if (!S[w] && (Dist[v] + G[v][w]) < Dist[w])
{
Dist[w] = Dist[v] + G[v][w];
Path[w] = v;
}
}
}
void DisplayPath(string name[], int begin, int temp)
{
if(begin == temp) {
cout << name[temp] ;
return ;
};
if (Path[temp] != -1)
{
DisplayPath(name, begin, Path[temp]);
cout << "-->"<< name[temp] ;
}
}
int main(){
// 邻接矩阵
int G[8][8] = {
{0,6,MaxInt,1,MaxInt,50,MaxInt,MaxInt},//v1
{MaxInt,0,43,11,6,MaxInt,MaxInt,MaxInt},//v2
{MaxInt,MaxInt,0,MaxInt,MaxInt,MaxInt,MaxInt,8},//v3
{MaxInt,MaxInt,MaxInt,0,12,MaxInt,MaxInt,MaxInt},//v4
{MaxInt,MaxInt,MaxInt,MaxInt,0,MaxInt,24,MaxInt},//v5
{MaxInt,MaxInt,MaxInt,MaxInt,1,0,12,MaxInt},//v6
{MaxInt,MaxInt,MaxInt,MaxInt,MaxInt,MaxInt,0,20},//v7
{MaxInt,MaxInt,MaxInt,MaxInt,MaxInt,MaxInt,MaxInt,0}//v8
};
string name[8];
for(int i = 0;i <8;i++){
name[i] ="v"+to_string(i+1);
// cout<<name[i]<<endl;
}
ShortestPath_DIJ(G,0,8);
// for(auto v:Path){
// cout<<v<<endl;
// }
DisplayPath(name, 0, 7);
cout<<endl<<"距离为"<<Dist[7]<<endl;
}



















 3401
3401

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








