一、实验目的:
理解递归算法的思想和递归程序的执行过程,并能熟练编写递归程序。
掌握分治算法的思想,对给定的问题能设计出分治算法予以解决。
二、实验环境:
VC6.0
三、实验内容:
1. Fibonacci数列
无穷数列1,1,2,3,5,8,13,21,34,55,……,称为Fibonacci数列。它可以递归地定义为:
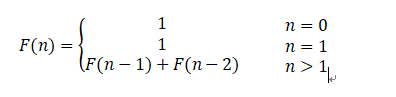
第n个Fibonacci数可递归地计算如下:
int fibonacci(int n)
{
if (n <= 1) return 1;
return fibonacci(n-1)+fibonacci(n-2);
}
- 编写完整的主函数,分别记录利用上述递归函数求第47, 48, 49, 50, 51,52个Fibonacci数所花费的时间。
#include<stdio.h>
#include<time.h>
int fi(int n)
{
if(n<=1) return (n);
else
return(fi(n-1)+fi(n-2));
}
int main()
{ int i;
double X;
X= clock()/CLOCKS_PER_SEC;
for(i=47;i<=52;i++)
{ X= clock()/CLOCKS_PER_SEC;
printf("计算第%d个数 所计算得的结果为%ld\t",i,fi(i));
X= clock() / CLOCKS_PER_SEC-X;
printf("计算第%d个的需要的时间为:%f\n",i,X);
}
}
- 将递归函数改为尾递归,或者是递推函数,求第47, 48, 49, 50, 51,52个Fibonacci数所花费的时间,观察效率是否得到提高。
#include<stdio.h>
#include<time.h>
double fi(int n)
{
double F;
int Fa,Fb;
Fa=0;
Fb=1;
for(int i=0;i<n;i++){
F=Fa+Fb;
Fb=Fa;
Fa=F;
}
return F;
}
int main()
{
int i;
double X;
X= clock()/CLOCKS_PER_SEC;
for(i=47;i<=52;i++)
{
X= clock()/CLOCKS_PER_SEC;
printf("计算第%d个数 所计算得的结果为%ld\t",i,fi(i));
X= clock() / CLOCKS_PER_SEC-X;
printf("计算第%d个的需要的时间为:%f\n",i,X)
}
return 0;
}
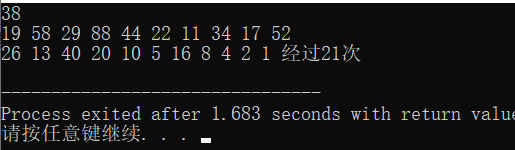
2.角谷定理。
输入一个自然数n,若n为偶数,则把它除以2,若n为奇数,则把它乘以3加1。用新得到的数重复以上步骤,直到值为1为止。求经过多少次看得到自然数1。
#include <iostream>
using namespace std;
int w = 0;
int jg(int n){
if (n == 1)
{
return 0;
}
else if (n % 2 == 0)
{ n /= 2;
cout<<n<<" ";
if(w==9)
cout<<endl;
w++;
return jg(n);
}
else
{ n = n * 3 + 1;
cout<<n<<" ";
if(w==9)
cout<<endl;
w++;
return jg(n);
}
}
int main() {
int n;
cin >> n;
jg(n);
cout << 经过"<<w <<"次"<< endl;
return 0;
}
实验结果:
3.走台阶
有n级台阶,可以一步上一个台阶,也可以一步上两个台阶,编写程序,计算共有几种不同的走法。
#include <iostream>
using namespace std;
int w = 0;
int Step(int n){
if (n < 0)
return 0;
if (n == 0){
w++;
return 0;
}
Step(n - 1);
Step(n - 2);
return 0;
}
int main() {
int n;
cin >> n;
Step(n);
cout << "有"<<w <<"种走法"<< endl;
return 0;
}
实验结果:

4. 半数集问题
问题描述:给定一个自然数n,由n开始可以依次产生半数集set(n)中的数如下:
(1) 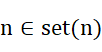 ;
;
(2) 在n的左边加上一个自然数,但该自然数不能超过最近添加的数的一半;
(3) 按此规则进行处理,直到不能再添加自然数为止。
例如,set(6)={6,16,26,126,36,136},半数集set(6)中有6个元素。
输入:整数n(0<n<1000)
输出:半数集set(n)中的元素个数。
请设计递归函数,求出set(n)的个数,并分析算法时间复杂度,对算法进行改进,用程序验证递归算法,以及改进之后的算法。
#include<iostream>
#include<time.h>
using namespace std;
int set(int n)
{
int a=1;
if(n>1)
for(int i=1;i<=n/2;i++)
a=a+set(i);
return a;
}
int main()
{
int n;
cout<<"请输入n值:";
cin>>n;
X= clock()/CLOCKS_PER_SEC;
cout<<"set("<<n<<")的个数为:"<<set(n)<<endl;
X= clock() / CLOCKS_PER_SEC-X;
cout<<"花费的时间为:"<<X<<endl;
return 0;
}
实验结果:
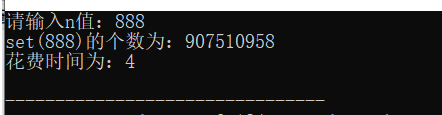
改进:
#include<iostream>
#include<cstring>
#include<time.h>
using namespace std;
int a[1000];
long set(int n)
{
int an=1;
if(a[n]>0)
return a[n];
for(int i=1;i<=n/2;i++)
an=an+set(i);
a[n]=an;
return an;
}
int main()
{
int n;
double X;
cout<<"ÇëÊäÈënÖµ£º";
cin>>n;
memset(a,0,sizeof(a));
a[1]=1;
X= clock()/CLOCKS_PER_SEC;
cout<<"set("<<n<<")的个数为:"<<set(n)<<endl;
X= clock() / CLOCKS_PER_SEC-X;
cout<<"花费的时间为:"<<X<<endl;
return 0;
}
实验结果:
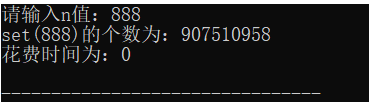




 本文探讨了递归算法在计算Fibonacci数列中的应用,比较了递归、尾递归和递推方法的效率。接着,通过角谷定理实例演示了分治策略,并针对走台阶和半数集问题进行了递归与优化算法的实现。最后,分析了半数集问题的改进算法及其时间复杂度。
本文探讨了递归算法在计算Fibonacci数列中的应用,比较了递归、尾递归和递推方法的效率。接着,通过角谷定理实例演示了分治策略,并针对走台阶和半数集问题进行了递归与优化算法的实现。最后,分析了半数集问题的改进算法及其时间复杂度。
















 787
787

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








