【排序算法】堆排序(Heapsort)

✨✨✨专栏：排序算法 

          🧑‍🎓个人主页：SWsunlight

目录

​编辑

前言：

一、堆排序：

时间复杂度：

空间复杂度：

算法稳定性：

二、升序的实现：通过建大堆实现

>思路：

1、向上调整算法实现大堆的建立：了解即可

 2、向下调整算法实现大堆的建立：

 3、排序：

 代码实现升序：

三、降序的实现：通过建小堆实现

>思路：

1、向上调整算法实现小堆的建立：了解即可

​编辑

2、向下调整算法实现小堆的建立：

​编辑

3、排序：

代码：

四、建堆的时间复杂度计算：

五、总结：

---

---

前言：

        本文基于对堆已经理解并通过代码实现后进行的，不知道堆的可以看上篇文章：堆

一、堆排序：

概念：   堆排序(Heapsort)是指利用 堆 这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。

利用了堆的特点：堆分为大根堆和小根堆，是完全二叉树。为啥升序大堆，降序小堆：大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。相反小堆最小值一定在堆顶；

时间复杂度：

        堆排序包括构建堆和排序两个操作：
        构建堆的时间复杂度：              T(n) = O(n)
        排序过程的时间复杂度：         ​​​​  T(n) = O(nlog2n)
        堆排序整体的时间复杂度：       T(n) = O(nlog2n)

空间复杂度：

         O(1)     实现排序不需要额外的空间，就是以数组自身的空间进行的

算法稳定性：

           堆的调整过程中，值相同的结点在比较过程中不能保证顺序，所以堆排序是一种不稳定的排序方法

二、升序的实现：通过建大堆实现

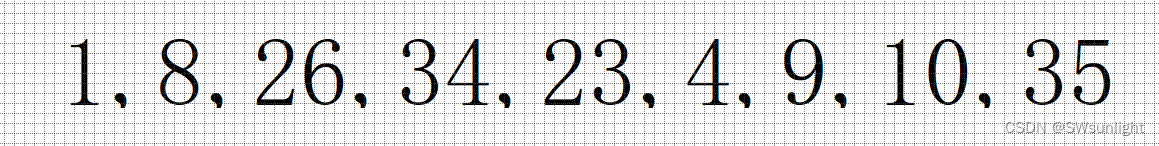
>思路：

1. 将待排序数组构造成一个大堆
2. 这个序列最大值在堆顶
3. 将其与末尾元素进行交换，末尾变成最大值
4. 将剩下的n-1个结点重新调整为大堆
5. 再次将最大值与新的末尾元素（此时有n-1个结点）交换
6. 重复下去，到最后就是有序的了，整个数组最小的元素此时在栈顶

1、向上调整算法实现大堆的建立：了解即可

我们将上图数组的第一个元素作为堆顶（即下标为0的元素），进行建堆，然后将第二个数据看成是插入堆（会进行比较，谁大谁会放到堆顶），依次类推，直到数组的最后一个元素，就是模拟的大堆进行插入操作，只是这些值已经有了，相当于插好了，只是需要进行调整

如下是我们将数组在逻辑结构上画成堆的样子，但不是堆，不满足堆的性质，所以需要我们进行