【数据结构】平衡二叉树AVLtree_平衡二叉树插入结点复杂度-优快云博客

本文链接：https://blog.youkuaiyun.com/SWELER/article/details/125030169

本文深入讲解AVL树的基本概念及其实现细节，包括左旋、右旋等平衡操作，以及插入、删除等关键操作的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

基本概念

一般来说（如图1），二叉查找树的查找操作的时间复杂度为O（log2（n））但是，如果我们每次插入数据都在二叉树的一侧（如图2），那么二叉查找树就会退化成一个链表，查找操作的时间复杂度为O（n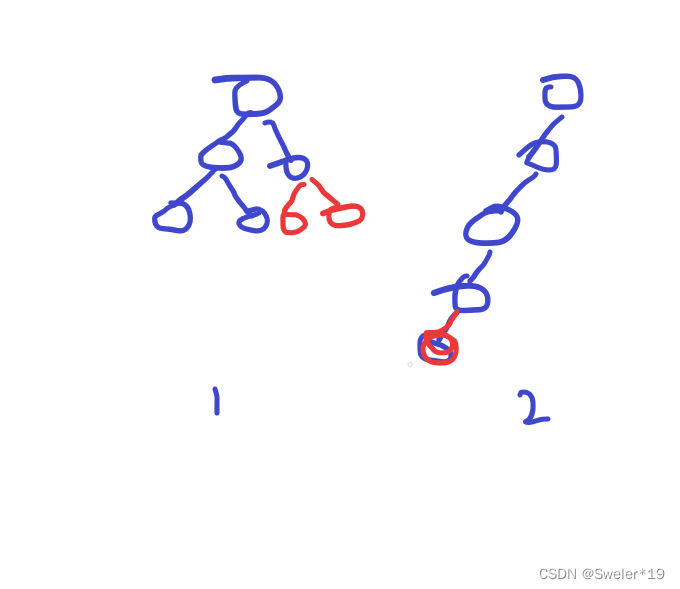）。请添加图片描述如何避免这种情况？需要在每次插入后从下往上逐个调整树的结构。图示是其中一种调节方法，经过调节后，根节点的两边子树高度差不会超过1，查找效率大大提高。

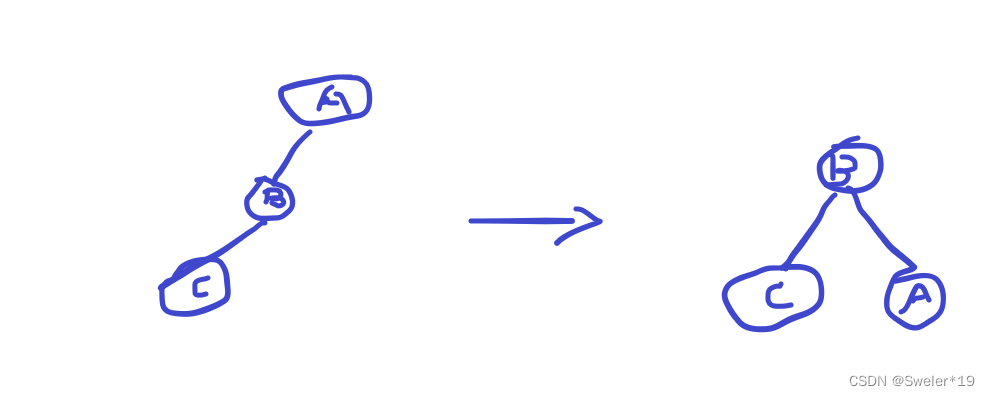
代码实现

和普通二叉树类似的，每个树节点都包含一个数据元素，一个左子树和一个右子树，另外还需要一个记录此树高度的数据height。

typedef int T;

struct AVLNode {
	T elem;
	struct AVLNode * lchil;
	struct AVLNode * rchil;
	int height;

};
typedef struct AVLNode* AVLTree;

需要实现的操作：
初始化、是否为空、求大小、求高度、前序后序中序遍历、清空、插入，删除。还需要有修复。

void initAVLTree(AVLTree *ptree);
bool emptyAVLTree(AVLTree tree);
size_t sizeAVLTree(AVLTree tree);
size_t heightAVLTree(AVLTree tree);
void foreachPrevAVLTree(AVLTree tree,void (*func)(T));
void oreachMidAVLTree(AVLTree tree,void (*func)(T));
void foreachBackAVLTree(AVLTree tree,void (*func)(T));

void clearAVLTree(AVLTree *ptree);
int insertAVLTree(AVLTree *ptree,T elem);
int insertAVLTreeCallSelf(AVLTree *ptree,T elem);
int deleteAVLTree(AVLTree *ptree,T elem);
int deleteAVLTreeCallSelf(AVLTree *ptree,T elem);

求高度我们用两个宏函数，HEIGHT用于正确的获取一个节点的height，REHEIGHT 用于在做修改之后重新确定树的高度，具体操作是获取左右子树中最高的高度再加一。

#define HEIGHT(node) (node==NULL?0:node->height)
#define REHEIGHT(node) (HEIGHT(node->lchil)>HEIGHT((node)->rchil)?HEIGHT((node)->lchil)+1:HEIGHT((node)->rchil)+1)

是否为空：返回tree==NULL
求大小：递归，tree为NULL返回0，返回左右子树size之和加1
求高度：用前面定义的宏函数

bool emptyAVLTree(AVLTree tree){
	assert(tree!=NULL);
	return tree==NULL;
}
size_t sizeAVLTree(AVLTree tree){
	if (tree==NULL) return 0;
	return sizeAVLTree(tree->lchil) + sizeAVLTree(tree->rchil)+1;
}
size_t heightAVLTree(AVLTree tree){
	return HEIGHT (tree);
}

前中后遍历：前面章节有介绍，这里略。

void foreachPrevAVLTree(AVLTree tree,void (*func)(T)){
	if(tree!=NULL){
		func(tree->elem);
		foreachPrevAVLTree(tree->lchil,func);
		foreachPrevAVLTree(tree->rchil,func);
	}
}
void foreachMidAVLTree(AVLTree tree,void (*func)(T)){
	if(tree!=NULL){
		foreachMidAVLTree(tree->lchil,func);
		func(tree->elem);
		foreachMidAVLTree(tree->rchil,func);
	}
}
void foreachBackAVLTree(AVLTree tree,void (*func)(T)){
	if(tree!=NULL){
		foreachBackAVLTree(tree->lchil,func);
		foreachBackAVLTree(tree->rchil,func);
		func(tree->elem);
	}
}

清空，解释略


void clearAVLTree(AVLTree *ptree){
	assert(ptree!=NULL);
	if(*ptree!=NULL){
		clearAVLTree(&(*ptree)->lchil);
		clearAVLTree(&(*ptree)->rchil);
		*ptree=NULL;
	}
}

建立一个节点，略

static struct AVLNode * createAVLNode(T elem,struct AVLNode *lchil,struct AVLNode * rchil,int height){
	struct AVLNode * node=malloc(sizeof(struct AVLNode));
	if(node!=NULL){
		node->lchil=lchil;
		node->rchil=rchil;
		node->elem=elem;
		node->height=height;
	}
	return node;
}

注意，重点来了

树的左旋、右旋

LL旋转（右旋）：树的左子树的左子树过高、
下面是示意图。
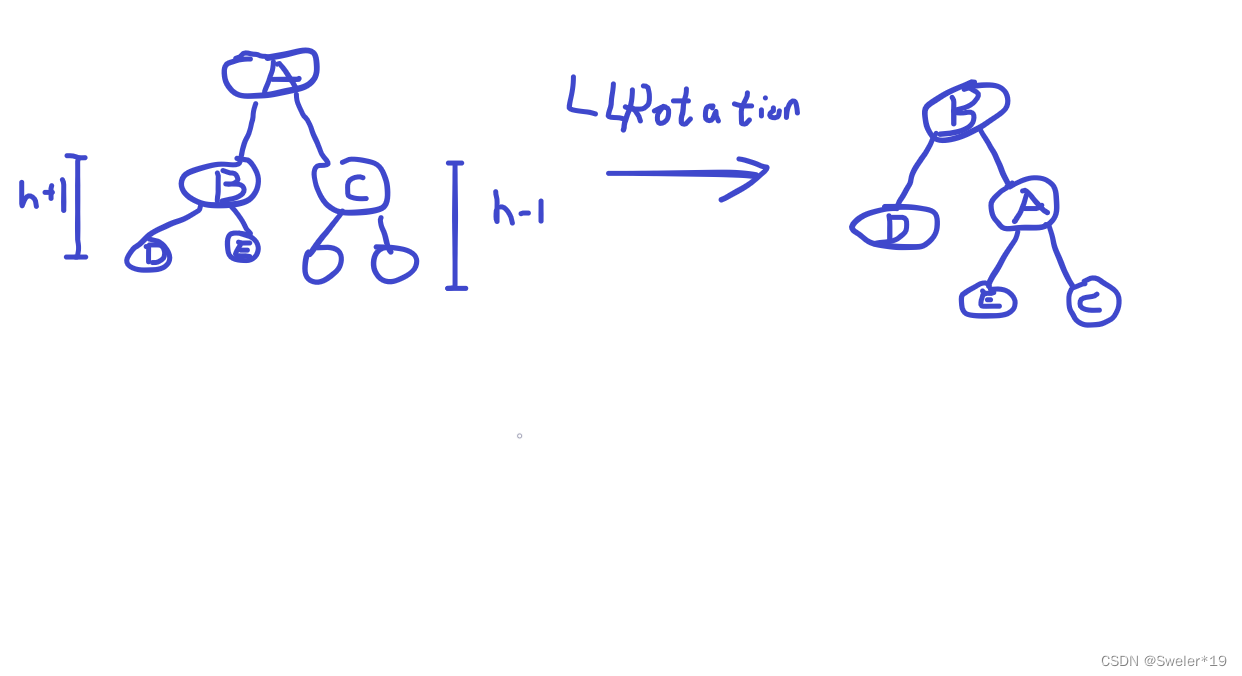
请添加图片描述
记录node的左子树为left，node左子树接left的右子树，left的右子树接node，调整之后需要更新node和left的高度，返回left（旋转之后的根节点）。

static struct AVLNode *LL_rotation(struct AVLNode * node){
	struct AVLNode * left=node->lchil;
	node->lchil=left->rchil;
	left->rchil=node;
	node->height=REHEIGHT(node);
	left->height=REHEIGHT(left);
	return left;
}

RR旋转（左旋）：树的右子树的右子树过高。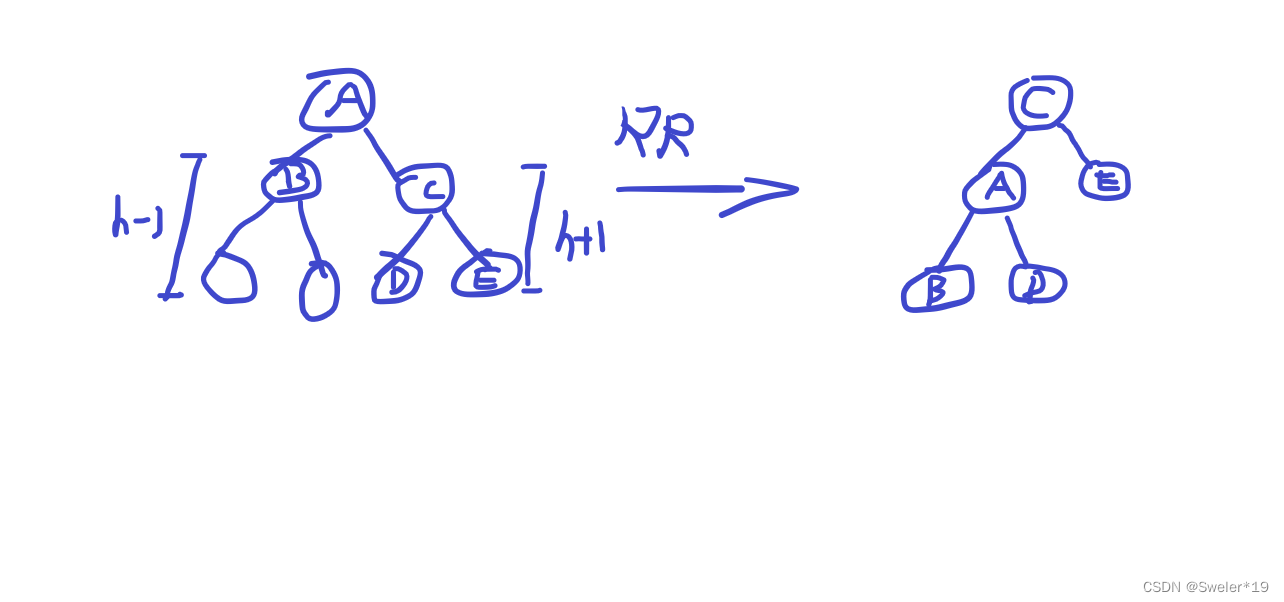请添加图片描述
记录node的右子树为right，node的右子树接right的左子树，right的左子树接node，更新高度，返回right

static struct AVLNode * RR_rotation(struct AVLNode * node){
	struct AVLNode * right=node->rchil;
	node->rchil=right->lchil;
	right->lchil=node;
	REHEIGHT(node);
	REHEIGHT(right);
	return right;
}

LR旋转（先左转再右转）
这里是图中c节点的左子树高了。
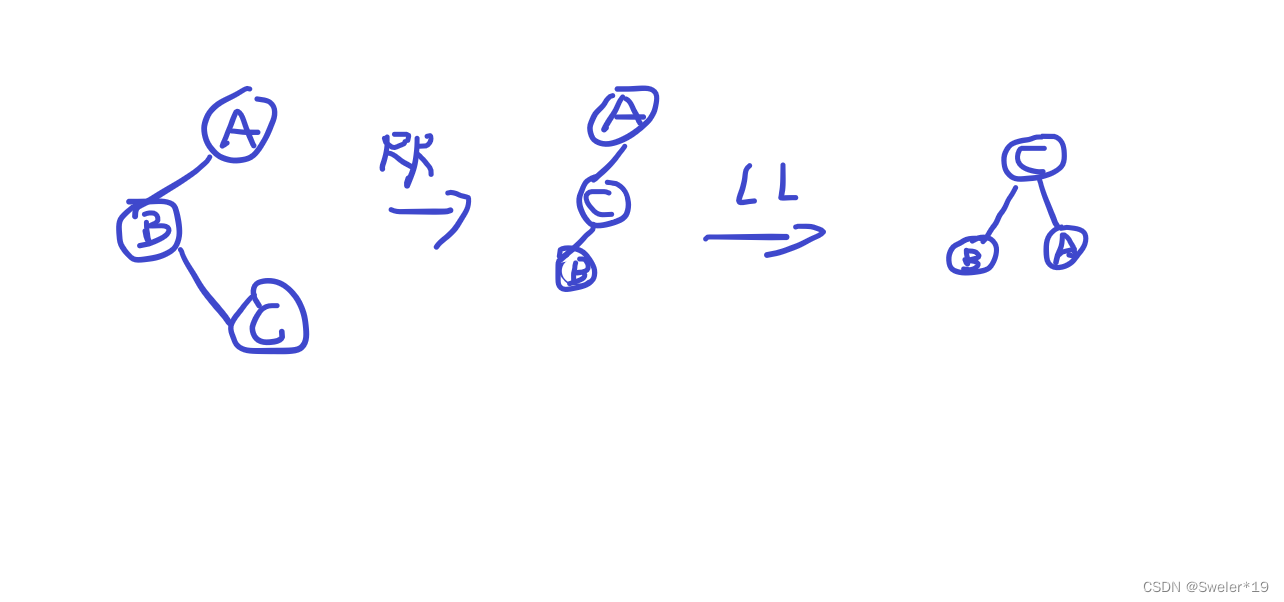请添加图片描述先给node的左子树左转，再对node右转

static struct AVLNode * LR_rotation(struct AVLNode * node){
	node->lchil=RR_rotation(node->lchil);
	return LL_rotation(node);
}

RL旋转：先左转再右转
这里是c节点的右子树高了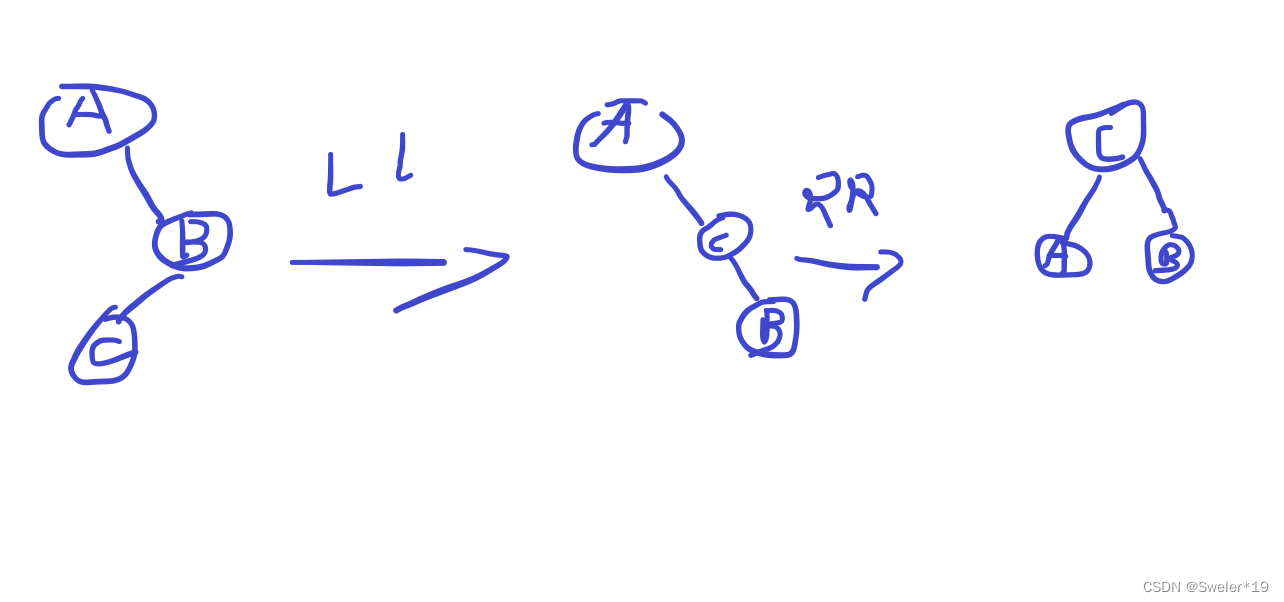请添加图片描述
先给node的右子树右转，也就是右转图中的B，转完之后C和B交换了位置，再对node左转。

static struct AVLNode * RL_rotation(struct AVLNode * node){
	node->rchil=LL_rotation(node->rchil);
	return RR_rotation(node);
}

修复：传入节点的地址的地址，定义平衡系数bn，bn为左子树高度减右子树高度。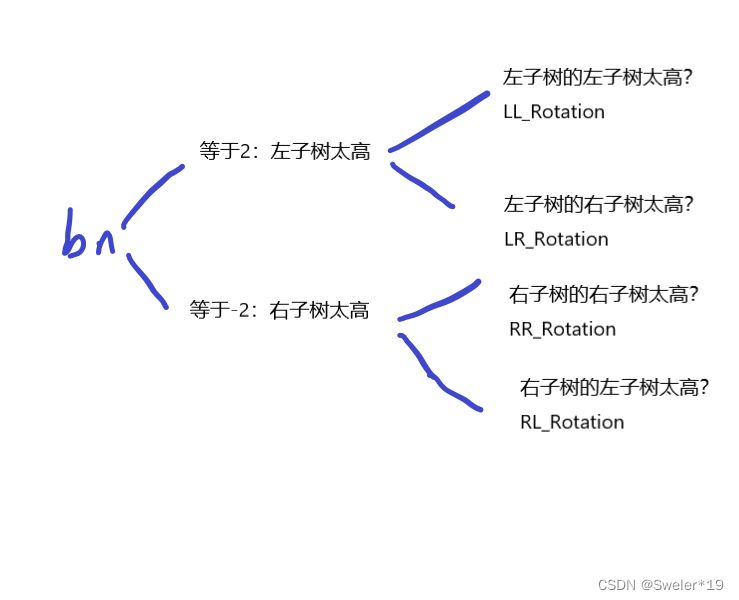请添加图片描述

void repairAVLTree(AVLTree * ptree){
	struct AVLNode * node=* ptree;
	int bn=HEIGHT(node->lchil)-HEIGHT(node->rchil);
	if(bn==2){
		int llh=HEIGHT(node->lchil->lchil);
		int lrh=HEIGHT(node->lchil->rchil);
		if(llh>lrh){
			*ptree=LL_rotation(*ptree);
		}else{
			*ptree=LR_rotation(*ptree);
		}
	}
	else if(bn==-2){
		int rlh=HEIGHT(node->rchil->lchil);
		int rrh=HEIGHT(node->rchil->rchil);
		if(rlh>rrh){
			*ptree=LR_rotation(*ptree);
		}
		else{
			*ptree=RL_rotation(*ptree);
		}
	}
}

插入：需要用到栈，传入根节点的地址的地址，要插入的元素。
在循环里，每次循环将当前节点入栈，判断插入元素是否大于当前节点元素。若小于，当前节点变为左子树，否则变为右子树，一样的话就清空栈退出（假设不允许插入相同元素。）在这个循环结束后，我们得到了一个适合插入元素的空叶子节点的位置，在这个位置创建节点。最后从栈里逐个弹出元素并修复。

#include"stack.h"
int insertAVLTree(AVLTree *ptree,T elem){
	Stack s;
	initStack(&s);
	while(*ptree!=NULL){
		pushStack(&s,ptree);
		if(elem<(*ptree)->elem){
			ptree=&(*ptree)->lchil;

		}else if(elem>(*ptree)->elem){
			ptree= &(*ptree)->rchil;
		}
		else {
			clearStack(&s);
			return FAILURE;
		}
	}
	*ptree =createAVLNode(elem,NULL,NULL,1);
	if(*ptree==NULL){
		clearStack(&s);
		return FAILURE;
	}
	while(!emptyStack(&s)){
		popStack(&s,&ptree);
		repairAVLTree(ptree);
		(*ptree)->height=REHEIGHT((*ptree));

	}
	clearStack(&s);
	return SUCCESS;
}

递归插入：当节点为空，说明可以插入节点，创建节点。
否则，判断要插入数据是否大于当前节点数据，大于就调用此节点的右子树递归插入，小于就调用此节点左子树递归插入，每次调用递归后记录是否插入成功，然后修复上次调用递归插入的节点，并更新高度。

int insertAVLTreeCallSelf(AVLTree *ptree,T elem){
	assert(ptree!=NULL);
	if(*ptree==NULL){
		*ptree=createAVLNode(elem,NULL,NULL,1);
		if(*ptree==NULL){
			return FAILURE;
		}
		return SUCCESS;
	}
	int ret=0;
	if(elem<(*ptree)->elem){
		ret=insertAVLTreeCallSelf(&(*ptree)->lchil,elem);
	}
	else if(elem<(*ptree)->elem){
		ret=insertAVLTreeCallSelf(&(*ptree)->rchil,elem);
	}
	else{
		return FAILURE;
	}
	if(ret==SUCCESS){
		repairAVLTree(ptree);
		(*ptree)->height=REHEIGHT((*ptree));
	}
	return ret;

}

递归删除：判断要删除元素是否等于当前节点的元素,若是，判断当前节点是否同时有左右子树，若有，找到此节点左子树的最大值的子树，替换此节点的值，递归调用删除本函数，调用结束后修复，更新高度。若节点没有同时有左右节点，用其中一个替代，在free此节点。不等于的话，去调用相应的左右子树的递归删除，删除成功后修复、更新。
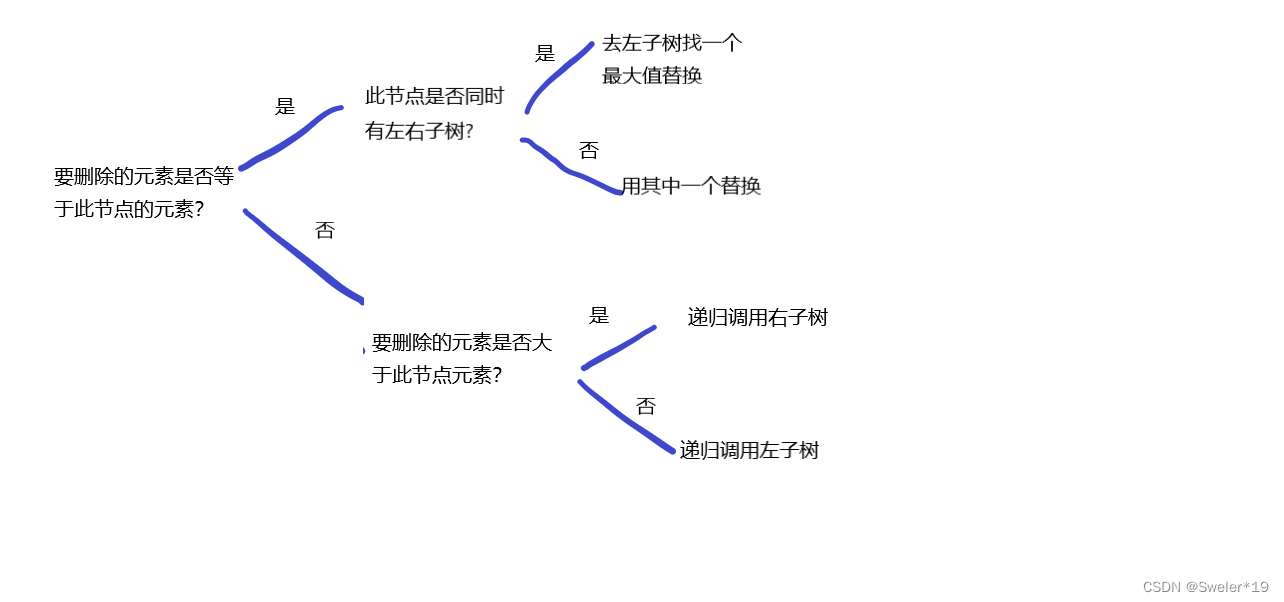
请添加图片描述

int deleteAVLTreeCallSelf(AVLTree *ptree,T elem){
	assert(ptree!=NULL);
	if(*ptree==NULL){
		return FAILURE;
	}
	if(elem==(*ptree)->elem){
		struct AVLNode * node=*ptree;
		if(node->lchil!=NULL&&node->rchil!=NULL){
			for(node=node->lchil;node->rchil!=NULL;node=node->rchil);
			(*ptree)->elem=node->elem;
			int ret=deleteAVLTreeCallSelf(&(*ptree)->lchil,node->elem);
			if(ret==SUCCESS){
				repairAVLTree(ptree);
				(*ptree)->height=REHEIGHT((*ptree));
			}
		}else{
			*ptree=node->lchil!=NULL?node->lchil:node->rchil;
			free(node);
		}
		return SUCCESS;
	}
	int ret=0;
	if(elem<(*ptree)->elem){
		ret=deleteAVLTreeCallSelf(&(*ptree)->lchil,elem);
	}else{
		ret=deleteAVLTreeCallSelf(&(*ptree)->rchil,elem);
		}
	if(ret==SUCCESS){
		repairAVLTree(ptree);
		(*ptree)->height=REHEIGHT((*ptree));
	}
	return ret;

}

删除：需要用栈。从当前节点开始遍历，每次循环将当前节点入栈，若节点元素等于要删除的元素，退出循环，若小于去左子树，若大于去右子树。假设遍历之后找到了要删除的节点，若此节点左右子树都不为空，用循环找到其左子树中最大值的节点，每次循环当前节点都入栈。循环结束，用找到的这个节点替换要删除的节点，再用左右子树替换它，再释放节点。最后把栈里的节点以此出栈，修复、更新高度。

int deleteAVLTree(AVLTree *ptree,T elem){
	Stack s;
	initStack(&s);
	while(*ptree!=NULL){
		pushStack(&s,ptree);
		if(elem==(*ptree)->elem){
			break;
		}else if(elem<(*ptree)->elem){
			ptree=&(*ptree)->lchil;
		}else{
			ptree=&(*ptree)->rchil;
		}

	}
	if(*ptree==NULL){
		clearStack(&s);
		return FAILURE;
	}
	struct AVLNode * node=*ptree;
	if(node->lchil!=NULL&&node->rchil!=NULL){
		for(ptree=&(*ptree)->lchil;(*ptree)->rchil!=NULL;ptree=&(*ptree)->rchil){
			pushStack(&s,ptree);
		}
		node->elem=(*ptree)->elem;
		node=*ptree;
	}
	*ptree=node->lchil!=NULL?node->lchil:node->rchil;
	free(node);
	popStack(&s,NULL);
	while(!emptyStack(&s)){
		popStack(&s,&ptree);
		repairAVLTree(ptree);
		(*ptree)->height=REHEIGHT((*ptree));
	}
	clearStack(&s);
	return SUCCESS;
}