视觉面经自用

原创已于 2025-06-16 21:26:41 修改 · 974 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#面试

于 2025-06-13 15:22:30 首次发布

部署运行你感兴趣的模型镜像

ViT

等待完善

Unet和分割

Unet网络结构

编码器 - 解码器结构：U - Net采用编码器 - 解码器的网络架构。编码器部分负责提取图像的特征，通常由多个卷积层和池化层组成。卷积层用于提取图像的局部特征，池化层则用于降低特征图的空间维度，同时保留重要的特征信息。随着网络的深入，特征图的空间分辨率逐渐减小，但通道数不断增加，从而能够捕捉到更抽象、更高级的特征。
跳跃连接（Skip Connections）：这是U - Net的一个关键特性。在解码器部分，网络通过跳跃连接将编码器中对应位置的特征图与解码器的特征图进行融合。这种连接方式可以有效地将编码器中提取的低层次、高分辨率的特征信息传递到解码器，从而有助于恢复分割目标的细节信息，提高分割的精度。
上采样操作：在解码器中，通过上采样操作逐步恢复特征图的空间分辨率。上采样可以通过多种方式实现，如反卷积层（转置卷积层）、最近邻插值等。上采样后的特征图与来自编码器的特征图进行融合，然后经过一系列的卷积操作进一步处理，最终得到分割结果。

介绍常用的分割损失函数

Bce-loss

criterion = nn.BCELoss()
loss = criterion(predictions, labels)

loss= -np.mean(label*np.log(oput) +(1-label)*np.log(1-oput))

Dice loss = 1-Dice

Dice loss = 1-Dice
Dice=

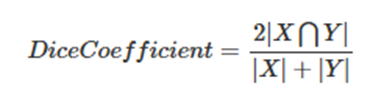
分割常用的评估方法

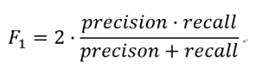
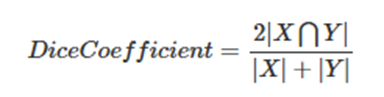
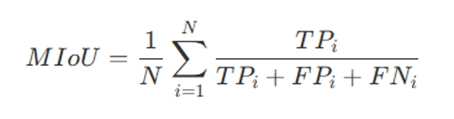
在这里插入图片描述

Swin-unet和unet 的区别

• UNet：

编码器-解码器结构：UNet 是一种经典的语义分割网络，采用编码器-解码器架构，通过卷积层和池化层逐步下采样特征图，再通过上采样和卷积层逐步恢复特征图的分辨率。
跳跃连接：通过跳跃连接将编码器的特征图与解码器的特征图拼接，以保留空间信息，避免因下采样导致的细节丢失。

• Swin-UNet：

纯 Transformer 架构：Swin-UNet 是第一个完全基于 Transformer 的 U 形架构。它将传统的卷积层替换为 Swin Transformer 块，用于提取分层特征。
窗口平移机制：Swin Transformer 引入了窗口平移机制，将注意力计算限制在当前区域附近的窗口内，从而更好地保留位置信息。
Patch 扩展层：在解码器中，使用 Patch 扩展层对特征图进行上采样，而不是传统的反卷积操作。

Mamba

状态空间模型，输入一个x和一个潜在的状态h

Yolo部分

介绍yolov8网络架构

• Backbone（骨干网络）Backbone 是 YOLOv8 的核心部分，负责从输入图像中提取特征。YOLOv8 的 Backbone 采用了类似于 CSPDarknet 的结构，具体为 CSPDarknet53 的变体。其主要特点包括：

C2f 模块：C2f 是 YOLOv8 中引入的一种新型模块，用于替代 YOLOv5 中的 C3 模块。它通过多分支结构和瓶颈设计，优化了梯度流，减少了冗余参数，同时保持了高效的特征提取能力。
空间金字塔池化模块（SPPF）：该模块通过不同大小的池化核对特征图进行处理，然后将结果拼接在一起，增加了感受野，能够更好地融合局部和全局特征，帮助网络学习多尺度的语义信息。

• Neck（颈部网络）Neck 位于 Backbone 和 Head 之间，主要用于特征融合和增强。YOLOv8 的 Neck 采用了路径聚合网络（PANet），它结合了特征金字塔网络（FPN）和 PANet 的优点，通过自下而上的路径机制，使得底层特征能够更顺畅地传递到高层，从而增强了对不同尺度目标的检测性能。
• Head（头部网络）Head 是 YOLOv8 的输出部分，负责将 Neck 输出的特征图转换为目标检测结果。YOLOv8 的 Head 采用了无锚点（Anchor-Free）设计的解耦检测头，将分类和检测任务分离为两个独立的分支：

分类分支：负责预测目标的类别概率。
回归分支：负责预测目标的边界框位置和尺寸。这种解耦设计使得模型能够更灵活地处理不同任务，提高了检测的准确性和效率。

Yolov8损失函数：

分类、回归、分割三个方面

分类损失（Classification Loss）
YOLOv8的分类损失通常采用二元交叉熵损失（Binary Cross-Entropy, BCE）或改进的交叉熵损失（Variational Focal Loss, VFL）。VFL是YOLOv8中引入的一种改进的损失函数，它通过引入非对称加权机制来突出正样本（即与真实框重叠较高的预测框）的重要性。VFL的公式如下： LVFL=−q⋅yi⋅ln(pi)−(1−yi)⋅ln(1−pi) 其中，q 是预测框与真实框的IoU（交并比），用于对正样本进行加权。
边界框回归损失（Bounding Box Regression Loss）
YOLOv8的边界框回归损失由CIoU损失（Complete IoU Loss）和分布焦点损失（Distribution Focal Loss, DFL）组成。
• CIoU损失：CIoU损失是一种改进的IoU损失，它不仅考虑了预测框和真实框的重叠面积，还引入了形状和尺度的惩罚项。CIoU损失的公式如下：
• 分布焦点损失（DFL）：DFL用于优化边界框的预测精度，它将边界框的位置建模为一个分布，使得网络能够更快速地聚焦于与目标位置距离较近的位置。
总损失函数（Total Loss）
YOLOv8的总损失函数是分类损失、边界框回归损失的加权和，具体公式如下： Ltotal=λclsLcls+λboxLbox+λdflLdfl 其中，λcls、λbox 和 λdfl 是各部分损失的权重。

图像进行训练之前的预处理方法

Resize 归一化裁剪旋转填充

介绍一下yolov8的nms

不想介绍

GAN网络

DCGAN

DCGAN对卷积神经网络的结构做了一些改变，以提高样本的质量和收敛的速度，这些改变有：

取消所有pooling层。G网络中使用转置卷积（transposed convolutional layer）进行上采样，D网络中用加入stride的卷积代替pooling。
在D和G中均使用batch normalization
去掉FC层，使网络变为全卷积网络
G网络中使用ReLU作为激活函数，最后一层使用tanh
D网络中使用LeakyReLU作为激活函数

GANs是一种以半监督方式训练分类器的方法，在没有很多带标签的训练集的时候，可以不做任何修改的直接使用GANs的代码

cGan

构建生成器
pix2pix cGAN 是经过修改的 U-Net。U-Net 由编码器（下采样器）和解码器（上采样器）。（有关详细信息，请参阅图像分割教程和 U-Net 项目网站。）
• 编码器中的每个块为：Convolution -> Batch normalization -> Leaky ReLU
• 解码器中的每个块为：Transposed convolution -> Batch normalization -> Dropout（应用于前三个块）-> ReLU
• 编码器和解码器之间存在跳跃连接（如在 U-Net 中）。
构建判别器
pix2pix cGAN 中的判别器是一个卷积 PatchGAN 分类器，它会尝试对每个图像分块的真实与否进行分类，如 pix2pix 论文中所述。
• 判别器中的每个块为：Convolution -> Batch normalization -> Leaky ReLU。
• 最后一层之后的输出形状为 (batch_size, 30, 30, 1)。
• 输出的每个 30 x 30 图像分块会对输入图像的 70 x 70 部分进行分类。
• 判别器接收 2 个输入：
• 输入图像和目标图像，应分类为真实图像。
• 输入图像和生成图像（生成器的输出），应分类为伪图像。
• 使用tf.concat([inp, tar], axis=-1) 将这 2 个输入连接在一起。

GAN缺点：

训练GAN需要达到纳什均衡,有时候可以用梯度下降法做到,有时候做不到。我们还没有找到很好的达到纳什均衡的方法
GAN不适合处理离散形式的数据，比如文本
GAN训练不稳定。

在博弈论中，纳什均衡是指在非合作博弈中，每个参与者都选择了最优的策略，前提是其他参与者的策略保持不变。

GAN训练问题

GAN为什么不好收敛

训练过程的复杂性
- GAN的训练是一个动态的、非线性的优化过程。生成器和判别器的更新是交替进行的，每次更新都会改变对方的优化目标。
- 生成器和判别器的优化目标是相互对抗的，这种对抗可能导致训练过程不稳定，甚至出现振荡。
模式崩溃（Mode Collapse）
- 模式崩溃是指生成器只生成少数几种类型的样本，而无法生成多样化的数据。这违反了纳什均衡的要求，因为生成器没有充分利用其策略空间。
- 模式崩溃使得生成器无法达到最优策略，进而无法达到纳什均衡。
训练的不完全性
- 实际训练中，生成器和判别器的网络结构和优化算法都有局限性。例如，网络的深度、宽度、学习率等超参数的选择都会影响训练结果。
- 由于这些限制，生成器和判别器可能无法达到理论上的最优策略，从而无法达到纳什均衡。
生成器梯度消失问题
- 当判别器D非常准确时，判别器的损失很快收敛到0，从而无法提供可靠的路径使生成器的梯度继续更新，造成生成器梯度消失。
- GAN的训练因为一开始随机噪声分布，与真实数据分布相差距离太远，两个分布之间几乎没有任何重叠的部分，这时候判别器能够很快的学习把真实数据和生成的假数据区分开来达到判别器的最优，造成生成器的梯度无法继续更新甚至梯度消失。

为什么GAN中的优化器不常用SGD

SGD容易震荡，容易使GAN 训练不稳定，GAN的目的是在高维非凸的参数空间中找到纳什均衡点，
GAN的纳什均衡点是一个鞍点，但是SGD 只会找到局部极小值，因为SGD解决的是一个寻找最小值的问题，GAN是一个博弈问题。

SGD和Adam

学习率调整

SGD：学习率是固定的，或者需要手动调整。在训练过程中，通常需要根据经验或学习率调度策略（如学习率衰减）来调整学习率。
Adam：学习率是自适应的。它根据梯度的一阶矩和二阶矩动态调整学习率，对不同参数使用不同的学习率。这种自适应特性使得Adam对初始学习率的选择不那么敏感。

内存占用

SGD：内存占用较小，因为它只需要存储当前的参数和梯度。
Adam：内存占用较大，因为它需要存储梯度的一阶矩和二阶矩的估计值。对于大规模模型，这可能会增加内存负担。

适用场景

SGD：
- 适用于大规模数据集，尤其是当数据量非常大时，SGD的计算效率高。
- 适用于简单的优化问题，如线性回归、逻辑回归等。
- 适用于对内存占用有限制的场景。
Adam：
- 适用于复杂的非凸优化问题，如深度神经网络训练。
- 适用于需要快速收敛的场景，尤其是在训练初期。
- 适用于对学习率调整不太敏感的场景。

激活函数：

激活函数的作用

引入非线性：这是激活函数最重要的作用。由于大多数实际问题都是非线性的，非线性激活函数使得神经网络能够拟合复杂的函数映射关系，从而解决非线性问题。
控制神经元输出范围：不同的激活函数有不同的输出范围，比如Sigmoid函数的输出在(0, 1)之间，Tanh函数的输出在(-1, 1)之间，ReLU函数的输出在[0, ∞)之间。这些特性有助于控制神经元的输出，防止数值不稳定。
加速训练：某些激活函数（如ReLU）具有计算效率高的优点，因为它们的计算只涉及到基本的算术操作，而不需要昂贵的指数运算。
缓解梯度消失/爆炸问题：一些激活函数（如ReLU及其变种）被设计来避免梯度消失或梯度爆炸问题，这些问题在训练深度神经网络时尤为突出。

RELU，leakrelu，tanh，sigmoid

1. Sigmoid

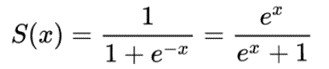
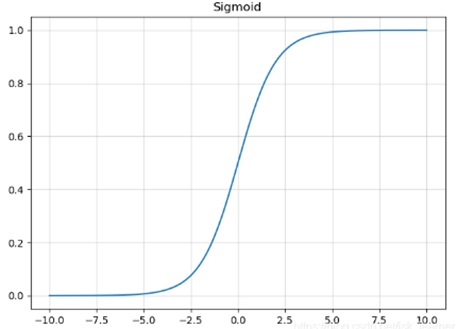
在这里插入图片描述

sigmoid优点
1. 输出范围明确：Sigmoid函数的输出范围在0到1之间，非常适合作为模型的输出函数。用于输出一个0到1范围内的概率值，比如用于表示二分类的类别或者用于表示置信度。
2. 便于求导：梯度平滑，便于求导，防止模型训练过程中出现突变的梯度。
sigmoid缺点
1. 梯度消失：导函数图像中，sigmoid的导数都是小于0.25的，那么在进行反向传播的时候，梯度相乘结果会慢慢的趋向于0。这样几乎就没有梯度信号通过神经元传递到前面层的梯度更新中，因此这时前面层的权值几乎没有更新。
2. 非零中心化输出：Sigmoid函数的输出不是以0为中心的，而是以0.5为中心。这意味着在训练过程中，输出值总是偏向正值，可能导致权重更新偏向于一个方向，会呈Z型梯度下降，影响学习效率。
3. 饱和性：Sigmoid函数的饱和性导致其在输入值的极端情况下对输入变化不敏感，这限制了网络对极端值的学习能力。
4. 计算资源消耗：Sigmoid函数涉及指数运算，这在计算上可能比其他一些激活函数（如ReLU）更加耗时。

2. Tanh

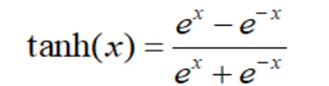
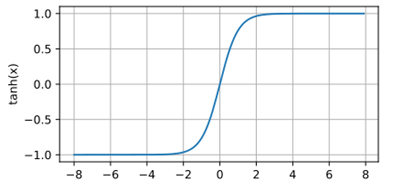
在这里插入图片描述

Tanh范围（-1,1），当输入在0附近时，tanh函数接近线形变换。函数的形状类似于sigmoid函数，tanh是“零为中心”的。因此在实际应用中，tanh会比sigmoid更好一些。

Tanh缺点：
1. 梯度消失问题：尽管Tanh函数在输入接近0时的梯度较大，但在输入值非常大或非常小的情况下，Tanh函数的导数仍然会接近0，导致梯度消失问题。
2. 计算资源消耗：Tanh函数涉及指数运算，这可能比其他一些激活函数（如ReLU）在计算上更加耗时。
3. 初始化敏感性：Tanh函数对权重初始化较为敏感，如果权重初始化不当，可能会导致梯度消失或爆炸问题。

3. Relu

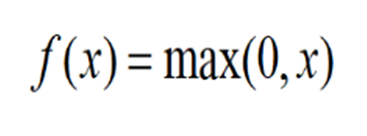
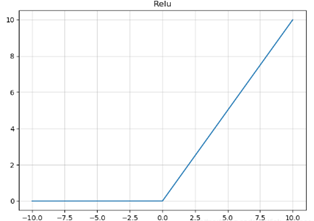
在这里插入图片描述

ReLU优点：
1. ReLU解决了梯度消失的问题，当输入值为正时，神经元不会饱和
2. 计算复杂度低，不需要进行指数运算
ReLU缺点：
1. 与Sigmoid一样，其输出不是以0为中心的
2. Dead ReLU 问题。当输入为负时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新

4. Leaky Relu

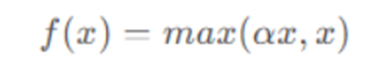
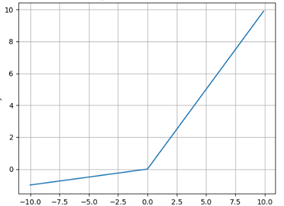
在这里插入图片描述

Leaky ReLU优点：
1. 解决了ReLU输入值为负时神经元出现的死亡的问题
2. 计算复杂度低，不需要进行指数运算
Leaky ReLU缺点：
1. 函数中的α，需要通过先验知识人工赋值（一般设为0.01）
2. 有些近似线性，导致在复杂分类中效果不好。

5. Softmax

Softmax 可以使正样本（正数）的结果趋近于 1，使负样本（负数）的结果趋近于 0；且样本的绝对值越大，两极化越明显。

Softmax层

softmax将输出的分类结果映射到（0-1）之间，将神经网络的分类结果转化成对应的概率。不同的概率，表示此样本属于对应类别的可能性大小，概率越大，样本属于该分类的可能性越大。概率的总和为1。

梯度消失和梯度爆炸：

梯度消失

梯度消失（Vanishing Gradient）定义

梯度消失是指在深层神经网络的反向传播过程中，当网络通过链式法则计算梯度以更新权重时，梯度值随着层数的增加而迅速减小，最终趋近于零。这会导致靠近输入层的权重更新变得非常缓慢，甚至几乎不更新，从而阻止网络从输入数据中学习有效的特征表示。

梯度消失的原因

梯度消失的主要原因包括激活函数的选择、链式法则的应用、权重初始化不当以及网络层数过多等。

激活函数的选择：在使用某些激活函数（如Sigmoid和Tanh）时，当输入值非常大或非常小的时候，这些函数的导数（或梯度）会趋近于零。
链式法则的应用：在深度神经网络中，梯度是通过链式法则从输出层逐层反向传播到输入层的。每一层的梯度都是前一层梯度与该层激活函数导数的乘积。如果每一层的梯度都稍微减小一点，那么经过多层传播后，梯度值就会变得非常小，几乎为零。
权重初始化不当：如果网络权重的初始值设置得太小，那么在前向传播过程中，输入信号可能会迅速衰减，导致激活函数的输入值非常小，进而使得梯度在反向传播过程中也迅速减小。
网络层数过多：随着网络层数的增加，梯度需要通过更多的层进行反向传播。每一层都可能对梯度进行一定的衰减，因此层数越多，梯度消失的风险就越大。

缓解梯度消失

为了缓解梯度消失问题，可以采取多种策略，如使用ReLU或其变体作为激活函数、采用合适的权重初始化策略、引入批量归一化（Batch Normalization）以及使用残差连接（Residual Connections）等。

梯度爆炸

梯度爆炸（Exploding Gradient）

梯度爆炸是指在反向传播过程中，梯度值随着层数的增加而迅速增大，最终变得非常大，超出了神经网络的正常处理范围，从而导致模型参数更新不稳定，甚至训练失败。

梯度爆炸的原因

梯度爆炸的原因主要包括权重初始化过大、网络层数过多以及学习率设置过高等。

权重初始化过大：在神经网络中，如果权重的初始值设置得过大，那么在反向传播过程中，梯度值可能会因为权重的累积效应而迅速增大，导致梯度爆炸。
网络层数过多：在深层神经网络中，由于链式法则的应用，梯度需要通过多层进行反向传播。如果每一层的梯度都稍微增大一点，那么经过多层传播后，梯度值就会变得非常大，导致梯度爆炸。
学习率设置过高：学习率决定了模型参数更新的步长。如果学习率设置得过高，那么模型参数在更新时可能会因为步长过大而跳出最优解的范围，同时过高的学习率会使模型在更新参数时过于激进，从而加剧梯度的波动。

残差连接如何缓解梯度消失

残差连接（Skip Connection）通过引入跨层恒等映射，重构了梯度的传播路径，成为解决梯度消失的关键技术。其设计可从以下多维度深入探讨：

结构设计：恒等映射与残差学习
基本形式：残差块的输出为 H ( x ) = F ( x ) + x，其中F ( x )为非线性变换（如多个卷积层），x为跳跃连接传递的原始输入。
核心思想：强制模型学习残差 F ( x ) = H ( x ) − x，而非直接映射 H ( x )。当目标函数接近恒等映射时，F ( x )趋近于零，易于优化。

归一化和标准化：

Min-max标准化（归一化）

z-score标准化（规范化）减均值除以方差

def Z_Score(data):
    lenth = len(data)
    total = sum(data)
    ave = float(total)/lenth
    tempsum = sum([pow(data[i] - ave,2) for i in range(lenth)])
    tempsum = pow(float(tempsum)/lenth,0.5)
    for i in range(lenth):
        data[i] = (data[i] - ave)/tempsum
    return date

Transformer

Transformer网络架构

整体架构
Transformer 网络主要由编码器（Encoder）和解码器（Decoder）组成。编码器将输入序列转换为上下文表示，解码器则利用这些上下文表示生成输出序列。编码器和解码器都由多个相同的层（Layer）堆叠而成。
编码器（Encoder）
编码器由多个相同的层堆叠而成，每一层包含两个主要模块：
- 多头自注意力机制（Multi-Head Self-Attention）：
  - 这是 Transformer 的核心模块，用于捕捉序列中不同位置之间的关系。
  - 输入序列会被分成多个“头”（Head），每个头学习序列的不同部分，然后将所有头的输出拼接起来。
  - 通过这种方式，模型能够同时关注序列中的多个位置，从而更好地理解上下文。
- 前馈神经网络（Feed-Forward Neural Network）：
  - 每个位置的输出都会经过一个全连接的前馈网络。
  - 这个网络对每个位置的特征进行非线性变换，进一步提取特征。
  - 每个编码器层的前馈网络是相同的，但参数是独立的。
解码器（Decoder）
解码器同样由多个相同的层堆叠而成，每一层包含三个主要模块：
- 掩码多头自注意力机制（Masked Multi-Head Self-Attention）：
  - 与编码器的多头自注意力类似，但加入了掩码（Mask）机制。
  - 掩码的目的是防止解码器在生成当前词时看到未来的信息，确保解码过程符合自然语言的生成顺序。
- 编码器 - 解码器注意力机制（Encoder-Decoder Attention）：
  - 这个模块将解码器的输出与编码器的输出进行交互。
  - 它允许解码器在生成每个词时参考编码器生成的上下文信息。
- 前馈神经网络（Feed-Forward Neural Network）：
  - 与编码器中的前馈网络类似，对每个位置的特征进行非线性变换。
位置编码（Positional Encoding）
由于 Transformer 不像循环神经网络（RNN）那样依赖序列的顺序，因此需要一种机制来引入位置信息。位置编码是一种向量，与输入嵌入（Embedding）相加，为模型提供每个词在序列中的位置信息。
输入和输出
- 输入：
  - 编码器的输入是经过嵌入和位置编码处理的输入序列。
  - 解码器的输入是目标序列的前缀（在训练时）或已生成的部分序列（在推理时）。
- 输出：
  - 解码器的输出是目标序列的概率分布，通过 softmax 函数计算每个词的生成概率。
优点
- 并行化：由于不依赖序列的顺序，Transformer 可以并行处理整个序列，训练速度更快。
- 捕捉长距离依赖：自注意力机制能够直接捕捉序列中任意位置之间的关系，适合处理长文本。
- 灵活性：Transformer 的架构可以应用于多种任务，如机器翻译、文本生成、问答系统等。

qkv公式
手写代码

CNN网络架构

输入层 → 卷积层 → 激活层 → 池化层 → 卷积层 → 激活层 → 池化层 → … → 全连接层 → 输出层

评估指标

AUC MAP recall precision

Recall

查全率（RECALL）——真正正样本中预测正确的比例
在这里插入图片描述

Precision

查准率（precision）——预测为正样本中的预测正确的比例
在这里插入图片描述

AUC

真正率：TPR——RECALL
真正率——正确预测为正样本的样本数占真正样本的比例
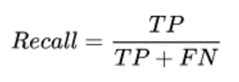
假正率：FPR = FP /（TN+FP）
假正率——错误预测为正样本的样本数占真负样本的比例
（和真正率的符号完全相反）
AUC——由TPR-FPR曲线（ROC）包围的面积
ROC曲线是通过改变分类的阈值，进而得到一系列的（TPR,FPR）的点，然后根据阈值从小到大得到的点绘制成TPR-FRP曲线，这条曲线称之为ROC曲线，然后计算曲线包围的面积，当面积越大时，说明性能越好。即AUC越大性能越好

mAP

P-R曲线——Precision和Recall组成的曲线
跟ROC曲线类似，改变阈值，得到一系列的RECALL和PRECISION点，绘制成的曲线。
AP
P-R曲线包围的面积称之为AP，AP越大性能越好
mAP（mean Average Precision）：所有类别的AP值取平均

LR逻辑回归

逻辑回归是一种广泛应用于二分类问题的线性分类模型，尽管它的名字中有“回归”二字，但它主要用于分类任务。逻辑回归的核心思想是通过一个线性组合来预测目标变量的概率，然后通过一个非线性的激活函数（如 Sigmoid 函数）将输出映射到 [0, 1] 区间，表示样本属于某个类别的概率。

损失函数

损失函数（Loss Function）是机器学习和深度学习中用于衡量模型预测值与真实值之间差异的函数。它的目的是通过量化这种差异，为模型训练提供优化的方向，使得模型能够更好地拟合数据。

均方误差（MSE）

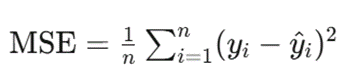
在这里插入图片描述

平均绝对误差（MAE）

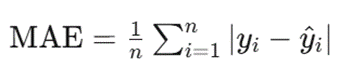
在这里插入图片描述

交叉熵损失（Cross-Entropy Loss）

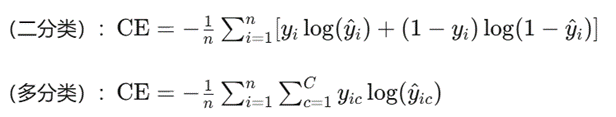
在这里插入图片描述

梯度，梯度下降，梯度下降优化算法

梯度是一个多变量函数在某一点处沿不同方向变化率的向量表示
梯度下降是一种优化算法，用于找到函数的最小值。其基本思想是：从一个初始点开始，沿着函数梯度的反方向（即函数值减小最快的方向）移动，逐步逼近函数的最小值点。

SGD ADAM

正则化

L1正则化和L2正则化的区别

L1正则化（Lasso）：
- 在损失函数中添加一个与模型权重的绝对值成正比的惩罚项。
L2正则化（Ridge）：
- 在损失函数中添加一个与模型权重的平方和成正比的惩罚项。
- L1正则化：通过将一些权重压缩到0，实现特征选择，适合高维数据。
- L2正则化：通过将权重变小，防止模型对某些特征过度依赖，适合低维数据。

过拟合处理方法，BN为什么能缓解过拟合

过拟合是指模型在训练数据上表现很好，但在新的、未见过的数据上表现不佳的现象。以下是几种常见的过拟合处理方法：

增加数据量：
- 方法：通过数据增强（如图像旋转、裁剪、翻转等）、数据合成或获取更多真实数据来扩大训练集。
- 原理：更多的数据可以提供更丰富的信息，减少模型对训练数据的过度拟合。
正则化：
- L1/L2正则化：在损失函数中添加正则化项，限制模型权重的大小。
- Dropout：在训练过程中随机丢弃一部分神经元，防止模型对某些神经元过度依赖。
- 原理：正则化方法通过限制模型的复杂度，减少模型对训练数据的过度拟合。
减少模型复杂度：
- 方法：减少模型的层数或每层的神经元数量。
- 原理：更简单的模型通常更容易泛化，不容易过拟合。
早停（Early Stopping）：
- 方法：在训练过程中，当验证集的损失不再下降时，停止训练。
- 原理：防止模型在训练集上过度拟合，同时保持在验证集上的良好性能。
BN缓解过拟合
内部协变量偏移的缓解：
- 内部协变量偏移：在深度神经网络中，每一层的输入分布会随着训练过程而变化，这种现象称为“内部协变量偏移”（Internal Covariate Shift）。这种变化会导致训练过程不稳定，模型更容易过拟合。
- BN的作用：通过归一化每一层的输入，BN可以减少内部协变量偏移的影响，使每一层的输入分布保持相对稳定，从而提高模型的泛化能力。

BN和LN的区别

Batch Normalization (BN)：
- 范围：对每个特征在小批量（mini-batch）内进行归一化。
Layer Normalization (LN)：
- 范围：对每个样本在同一层的所有特征上进行归一化。
  在图像处理任务中，BN由于其对批次大小的依赖性较小，通常是首选。而在NLP任务中，由于文本数据的复杂性和动态性，LN更为合适

面试问题：

手撕均值滤波
手撕卷积神经网络
手撕神经网络训练过程
力扣股票简单题
手撕mha
手撕transformer

1. 手撕均值滤波

filtered_image = cv2.blur(image, (kernel_size, kernel_size))
手撕代码：
# 定义均值滤波的核大小
kernel_size = 3  # 3x3 的窗口
padding = kernel_size // 2  # 计算填充大小
# 对图像进行边界填充，避免越界
padded_image = np.pad(image_array, ((padding, padding), (padding, padding)), mode='constant')

# 创建一个空的输出图像
filtered_image = np.zeros_like(image_array)

# 遍历每个像素点
for i in range(image_array.shape[0]):
    for j in range(image_array.shape[1]):
        # 提取当前像素点的邻域
        neighborhood = padded_image[i:i+kernel_size, j:j+kernel_size]
        # 计算邻域的平均值
        filtered_image[i, j] = np.mean(neighborhood)

2.手撕卷积：

def conv2olved(input_matrix, kernel, padding=0, stride=1):
    # 获取输入矩阵和卷积核的大小
    input_height, input_width = input_matrix.shape
    kernel_height, kernel_width = kernel.shape
    # 计算输出矩阵的大小
    output_height = (input_height - kernel_height + 2 * padding) // stride + 1
    output_width = (input_width - kernel_width + 2 * padding) // stride + 1
    # 初始化输出矩阵
    output_matrix = np.zeros((output_height, output_width))
    # 对输入矩阵进行填充
    padded_input = np.pad(input_matrix, pad_width=padding, mode='constant', constant_values=0)
    # 进行卷积操作
    for y in range(0, output_height):
        for x in range(0, output_width):
            # 计算当前卷积核覆盖的区域
            input_patch = padded_input[y * stride:y * stride + kernel_height, x * stride:x * stride + kernel_width]
            # 计算卷积核与输入区域的逐元素乘积之和
            output_matrix[y, x] = np.sum(input_patch * kernel)

    return output_matrix

您可能感兴趣的与本文相关的镜像

Yolo-v5

Yolo

YOLO（You Only Look Once）是一种流行的物体检测和图像分割模型，由华盛顿大学的Joseph Redmon 和Ali Farhadi 开发。 YOLO 于2015 年推出，因其高速和高精度而广受欢迎