代码随想录算法训练营第二十二天| 回溯算法理论基础、 77 组合、 216 组合总和III

回溯算法理论基础

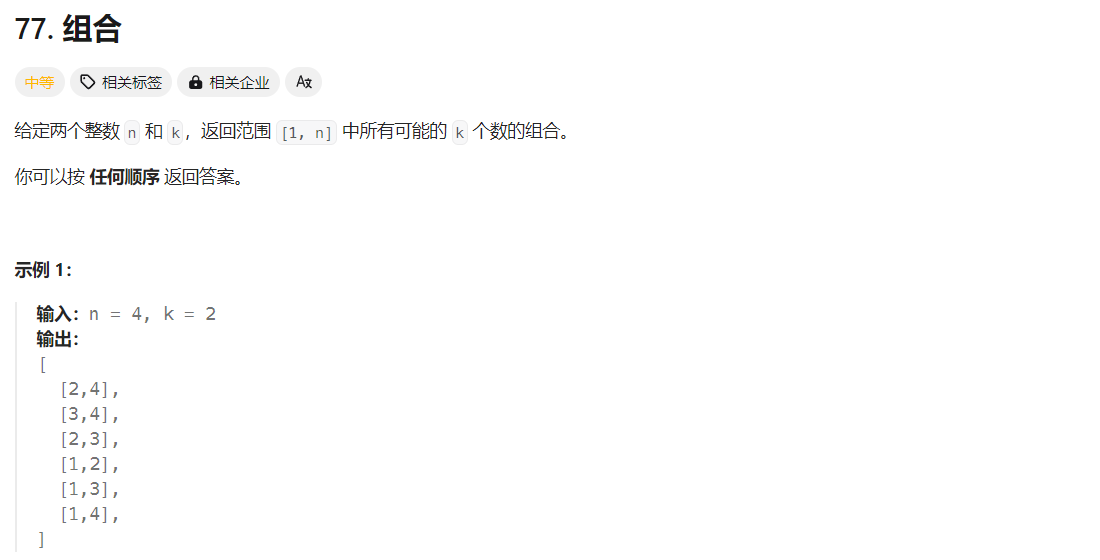
一、 77 组合

//C语言
int *path;//一维数组存放合适的组合，并且用于回溯
int pathSize;
int **result;//二维数组用于存放最终的所有结果
int resultSize;
void backtracking(int n,int k,int startindex){
    //n为元素个数，k为组合大小，startindex用于确定起始位置
    //确定终止条件
    if(pathSize == k){
        int *tmp = (int*)malloc(sizeof(int)*k);
        for(int i=0;i<k;i++)
            tmp[i]=path[i];
        result[resultSize++] = tmp;
        return;
    }
    //单层循环逻辑
    for(int j = startindex;j<=n-(k-pathSize)+1;j++){
        path[pathSize++] = j;//处理节点
        backtracking(n,k,j+1);//递归函数
        pathSize--;//回溯
    }
}
int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {
    path = (int*)malloc(sizeof(int)*k);
    result = (int**)malloc(sizeof(int*)*10000);
    pathSize = 0;
    resultSize = 0;
    backtracking(n,k,1);
    *returnSize = resultSize;
    *returnColumnSizes = (int*)malloc(sizeof(int) *(*returnSize));
    for(int i = 0; i < *returnSize; i++) {
        (*returnColumnSizes)[i] = k;
    }
    return result;
}
//C++
class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i<= n-(k-path.size()) + 1; i++) { // 优化的地方
            path.push_back(i); // 处理节点
            backtracking(n, k, i + 1);
            path.pop_back(); // 回溯，撤销处理的节点
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
};

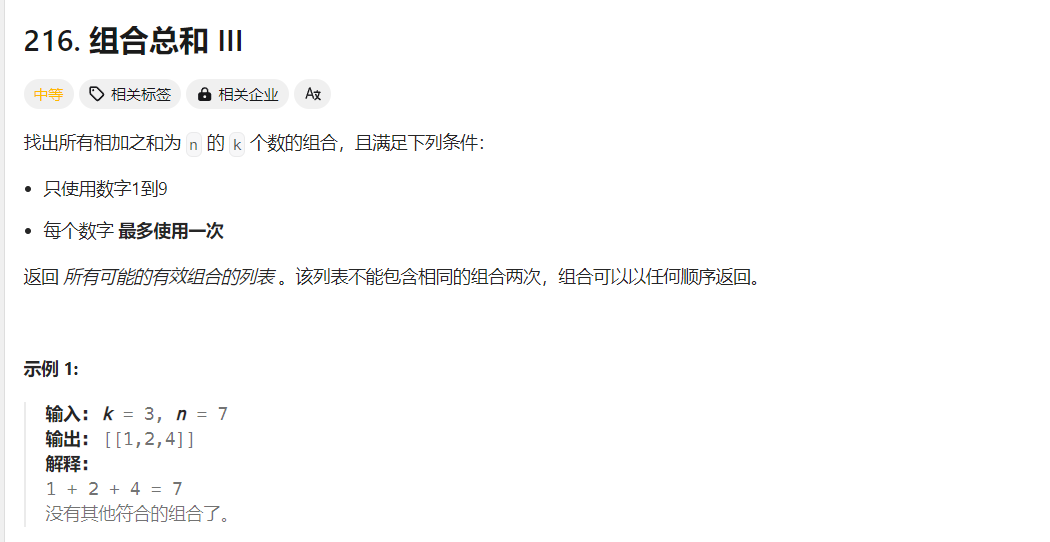
二、 216 组合总和III

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(int n, int k,int sum, int startIndex) {
        if (path.size() == k) {
            if(n == sum)
                result.push_back(path);
            else//剪枝
                return;
        }
        for (int i = startIndex; i<= 9; i++) { // 优化的地方
            sum += i;
            path.push_back(i); // 处理节点
            backtracking(n, k, sum,i + 1);
            sum -= i;
            path.pop_back(); // 回溯，撤销处理的节点
        }
    }
public:
    vector<vector<int>> combinationSum3(int k, int n) {
        backtracking(n,k,0,1);
        return result;
    }
};