粒子群优化算法，C#实现

粒子群算法是一门新兴算法，此算法与遗传算法有很多相似之处，其收敛于全局最优解的概率很大。
①相较于传统算法计算速度非常快，全局搜索能力也很强；
②PSO对于种群大小不十分敏感，所以初始种群设为500-1000，速度影响也不大；
③粒子群算法适用于连续函数极值问题，对于非线性、多峰问题均有较强的全局搜索能力。

作为举例说明，本文将用粒子群算法，求解Rastrigin函数f(x)=x²-10*cos(2πx)+10在区间[-6,6]的极小值。
先用matlab画出这个函数的图像，便于我们直观地观察：

该函数的全局最小值为0，在x=0处取得

下面，用C#实现求极值。测试环境VS2015

using System;
using System.Linq;
using System.Threading;

namespace PSO_FunctionTest
{

    class Program
    {
        public static double[] xlimit = new double[2] { -6, 6 };       //位置边界设置
        public static double[] vlimit = new double[2] { -2, 2 };       //速度边界设置
        
        public static int generation;             //迭代次数

         static void Main(string[] args)
        {
            int popsize;                  //种群规模         
            double Wmax=0.95;             //惯性权重设置
            double Wmin = 0.45;
            double C1 = 2;                //自我学习因子
            double C2 = 2;                //群体学习因子
            Random rand = new Random();
            
            Console.WriteLine("请输入种群规模大小：");
            popsize = Convert.ToInt32(Console.ReadLine());
            Console.WriteLine("请输入迭代次数:");
            generation = Convert.ToInt32(Console.ReadLine());
            Console.WriteLine("算法运行中，请稍后......");

            //参数初始化           
            double[] x0 = new double[popsize];                  //种群位置初始化
            double[] V = new double[popsize];                    //粒子速度初始化
            double[] x_pbest = new double[popsize];         //个体历史最好位置
            double[] p_fitness = new double[popsize];       //个体历史最佳适应度
            double x_gbest = new double();                        //群体历史最好位置
            double g_fitness = new double();                      //群体历史最佳适应度
            Initialize(popsize,out x0,out x_pbest, out p_fitness, out x_gbest, out g_fitness,out V);

            Thread.Sleep(3000);                                            //延时

            //算法运行
            for (int i = 0; i < generation; i++)
            {
                double[] fitness = new double[popsize];
                for (int j = 0; j < popsize; j++)
                {
                    fitness[j] =func(x0[j]);
                }
                //遍历每个粒子
                for (int j = 0; j < popsize; j++)
                {
                    if (fitness[j]<p_fitness[j])             //将当前个体适应度与个体历史最佳适应度比较，符合条件则替换
                    {
                        p_fitness[j] = fitness[j];            //更新个体历史最佳适应度
                        x_pbest[j] = x0[j];                     //更新对应位置
                    }
                }
                if (g_fitness>p_fitness.Min())
                {
                    g_fitness = p_fitness.Min();             //更新全局最优值
                    int index = new int();                      //在个体历史适应度中找到最小值的索引号
                    index = p_fitness.ToList().IndexOf(p_fitness.Min());      //索引值
                    x_gbest = x0[index];               //更新全局最好位置
                }
                double W = new double();
                W= Wmax - (Wmax - Wmin) * i / generation;     //线性递减惯性权重
                
                for (int j = 0; j < popsize; j++)
                {
                    //速度更新
                    V[j] = W * V[j] + C1 * rand.NextDouble() * (x_pbest[j] - x0[j]) + C2 * rand.NextDouble() * (x_gbest - x0[j]);
                    //速度限制
                    if (V[j]>vlimit[1])
                    {
                        V[j] = vlimit[1];
                    }
                    if (V[j]<vlimit[0])
                    {
                        V[j] = vlimit[0];
                    }
                    //位置更新
                    x0[j] = x0[j] + V[j];
                    //位置限制
                    if (x0[j]>xlimit[1])
                    {
                        x0[j] = xlimit[1];
                    }
                    if (x0[j] < xlimit[0])
                    {
                        x0[j] = xlimit[0];
                    }
                }
            }
            Console.WriteLine("目标函数的全局最小值是：{0}\n出现在x={1}处", g_fitness.ToString("f3"), x_gbest.ToString("f3"));
            Console.ReadKey();

        }
        /// <summary>
        /// 函数表达式
        /// </summary>
        /// <param name="variable">自变量</param>
        /// <returns>函数值</returns>
        public static double func(double variable)
        {
            double x = variable;
            double f;
            f = x * x - 10 * Math.Cos(2 * Math.PI * x) + 10;
            return f;
        }

        //初始化参数
        public static void Initialize(int popsize,out double[] x0,out double[] x_pbest,out double[] p_fitness,out double x_gbest,out double g_fitness,out double[] V )
        {
            Random rand = new Random();
            double[] x = new double[popsize];                     //种群位置
            double[] v0 = new double[popsize];                   //粒子速度
            //double[][] pbest = new double[popsize][];      //个体历史最好位置
            double[] p_fit = new double[popsize];                //个体历史最优值
            double gbest = rand.Next(0, 1);                          //群体历史最佳位置
            double g_fit = double.PositiveInfinity;                //群体历史最佳适应度

            for (int i = 0; i < popsize; i++)
            {                              
                x[i] = xlimit[0] + rand.NextDouble() * (xlimit[1] - xlimit[0]);
                v0[i] = rand.NextDouble();                
                p_fit[i] = rand.Next(1,2);              //个体历史最佳适应度初始化选取，需额外注意！！！！
            }           
            x0 = x;
            V = v0;
            x_pbest = x;
            p_fitness = p_fit;
            x_gbest = gbest;
            g_fitness = g_fit;
        }      
    }
}

调试运行，得到如下结果：

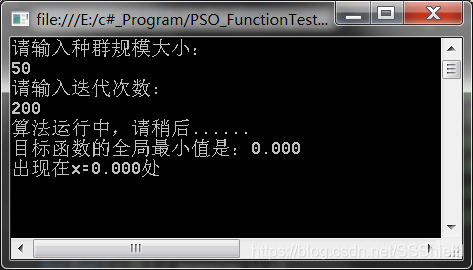
算法运行结果基本正确
本人初学，欢迎各位指正！！！