[DFS][打表]染色的立方体

最新推荐文章于 2022-03-08 19:00:47 发布

原创最新推荐文章于 2022-03-08 19:00:47 发布 · 341 阅读

0 ·

CC 4.0 BY-SA版权

本文介绍了一种通过重新涂色使多个立方体外观一致的算法。该算法利用搜索技术和贪心策略来确定最少的涂色次数，以实现所有立方体颜色的统一。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

小胖最近迷上了3D物体，尤其是立方体。他手里有很多个立方体，他想让所有的立方体全都长得一样，所以他决定给某些立方体的表面重涂颜色，使得所有的立方体完全相同。但是小胖是很懒的，他想知道最少涂多少次颜色，可以让所有立方体完全相同。

Input

输入包含多组数据，每组数据第一行n(1<=n<=4)，表示立方体的数量，接下来n行，每行6个字符串，表示立方体6个面的颜色:Color 1 Color 2 Color 3 Color 4 Color 5 Color 6,中间用一个空格隔开。
其中，面的标号如下：
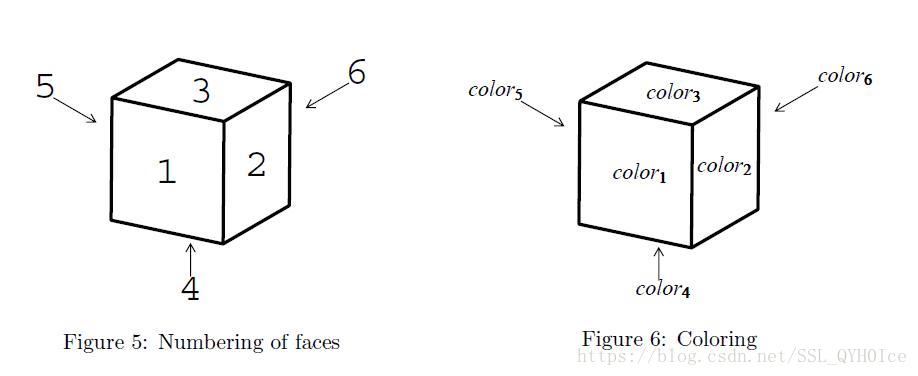
这里写图片描述

n=0表示输入结束。
两个立方体被视为相同，当且仅当他们可以在某种摆放方式下，每个面的颜色都对应相同。

Output

每组数据，输出一行一个整数，表示最少的涂色数。（涂一个面算一次涂色）

Sample Input

3
scarlet green blue yellow magenta cyan
blue pink green magenta cyan lemon
purple red blue yellow cyan green
2
red green blue yellow magenta cyan
cyan green blue yellow magenta red
2
red green gray gray magenta cyan
cyan green gray gray magenta red
2
red green blue yellow magenta cyan
magenta red blue yellow cyan green
3
red green blue yellow magenta cyan
cyan green blue yellow magenta red
magenta red blue yellow cyan green
3
blue green green green green blue
green blue blue green green green
green green green green green sea-green
3
red yellow red yellow red yellow
red red yellow yellow red yellow
red red red red red red
4
violet violet salmon salmon salmon salmon
violet salmon salmon salmon salmon violet
violet violet salmon salmon violet violet
violet violet violet violet salmon salmon
1
red green blue yellow magenta cyan
4
magenta pink red scarlet vermilion wine-red
aquamarine blue cyan indigo sky-blue turquoise-blue
blond cream chrome-yellow lemon olive yellow
chrome-green emerald-green green olive vilidian sky-blue
0

Sample Output

4
2
0
0
2
3
4
4
0
16

分析

~~也许是我做过的最难的模拟题~~
我们知道一个立方体对于那个编号方式，可以有很多不同的摆放
打表出来不就好了？
然后我们用爆搜，每搜齐n个就用贪心思想求出总需涂色数
这里偷懒：用map替代hash给字符串标个号

#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
#define rep(i,a,b) for (i=a;i<=b;i++)
using namespace std;
char c[101];
int a[5][7];
int r[5];
map<string,int> p;
int d[25][7]=
{
{0,0,0,0,0,0,0},
{0,3,2,6,1,5,4},
{0,3,1,2,5,6,4},
{0,3,5,1,6,2,4},
{0,3,6,5,2,1,4},
{0,5,3,6,1,4,2},
{0,6,3,2,5,4,1},
{0,2,3,1,6,4,5},
{0,1,3,5,2,4,6},
{0,1,2,3,4,5,6},
{0,5,1,3,4,6,2},
{0,6,5,3,4,2,1},
{0,2,6,3,4,1,5},
{0,6,2,4,3,5,1},
{0,2,1,4,3,6,5},
{0,1,5,4,3,2,6},
{0,5,6,4,3,1,2},
{0,2,4,6,1,3,5},
{0,1,4,2,5,3,6},
{0,5,4,1,6,3,2},
{0,6,4,5,2,3,1},
{0,4,5,6,1,2,3},
{0,4,6,2,5,1,3},
{0,4,2,1,6,5,3},
{0,4,1,5,2,6,3},
};
int n,i,j,l;
int ans;
void fresh()
{
    int p=0,rex,i,j;
    int cnt[25];
    rep(i,1,6)
    {
        rep(j,0,24) cnt[j]=0;
        rex=0;
        rep(j,1,n)
        {
            cnt[a[j][d[r[j]][i]]]++;
            rex=max(rex,cnt[a[j][d[r[j]][i]]]);
        }
        p+=n-rex;
    }
    ans=min(ans,p);
}
void dfs(int dep)
{
    int i;
    if (dep==n+1)
    fresh();
    else
    rep(i,1,24)
    {
        r[dep]=i;
        dfs(dep+1);
    }
}
int main()
{

    while (1)
    {
        scanf("%d",&n);
        ans=2147483647;
        if (n==0) break;
        p.clear();
        l=0;
        rep(i,1,n)
        rep(j,1,6)
        {
            scanf("%s",&c);
            if (!p[c])
            {
                l++;
                p[c]=l;
            }
            a[i][j]=p[c];
        }
        r[1]=1;
        dfs(2);
        printf("%d\n",ans);
    }
}