[利用性质的简单算法] 判断无向图是否为树

题目：判断一个无向图是否为树。

输入：

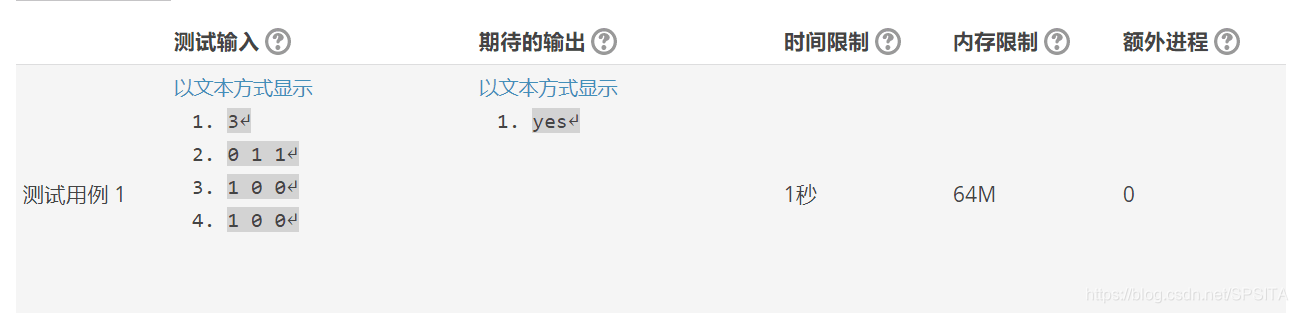
第一行为正整数n，代表图中点的个数；

接下来n行，每行有n个数据，每个数据以空格分隔，代表邻接矩阵。

输出：

若为树，输出yes；

否则，输出no。

首先来讲解树需要满足的性质
1：这个图里面不能有孤立的点，也就是说这应该是一个连通图。
2：n阶图里面边的数量应该是n-1。换句话来说，也就是两个点之间只有唯一的一条路径，当然，我们这里采用前一种描述方法。
3：图里面不应该有圈的存在。

特别注意，如果是平凡图，也就是只有一个点，没有任何边的时候，肯定是树

好的，现在开始根据三条性质来编程。
首先用二维数组的方式，来存储邻接矩阵。

首先，根据第一条性质： 矩阵的每一行都应该不是全部为0
的，如果全部都是0，就代表这是一个孤立点。

其次，通过第二条性质： 邻接矩阵当中所有的数字加在一起，应该是2（n-1），这是“握手定理”，所有点的出度和加上入度和是边数的两倍。很好理解，也就是矩阵里面，一条边会在两个点都出现，也就是计算了两次。如果所有数字加在一起不是2（n-1），那么就一定不是树

最后，分析第三条性质： 这也是根据这三个性质就可以得到答案的最关键的步骤。如果一个图里面存在圈会怎么样？如果存在圈的话，同时还满足第二条性质的话，就必然会有孤立点出现，也就是说一定会违反第一条判定规则。
特殊情况，还有一种情况可以满足三种判定条件，这就是当一个图中的点，存在一条自己到自己的边，也就是最小的圈。这个时候再加入一个特别的判定：point [ i ] [ i ] == 1的话，就一定不是树。

也就是说，这样的算法根本不需要dfs，而且多重的递归非常占用系统的内存，完全没有必要，只需要对输入的邻接矩阵进行分析就可以了，多利用数学的知识来解决问题，而不是编程知识。计算机和编程语言都是数学的工具。