本文深入探讨了朴素贝叶斯算法，一种基于生成式学习策略的机器学习算法。文章详细介绍了算法的理论基础，包括生成式模型与判别式模型的区别，以及贝叶斯定理在分类问题中的应用。朴素贝叶斯算法通过假设特征之间的独立性简化计算，简化版包括伯努利朴素贝叶斯、多项式朴素贝叶斯和高斯朴素贝叶斯。文中还通过代码实例展示了算法在MNIST手写数字识别和IMDb影评数据集分类任务中的应用，并分析了算法的优缺点。
全角度解析朴素贝叶斯(Naive Bayes)：一种基于生成式学习策略的机器学习算法
本篇博客的所有代码均已上传个人Github仓库：https://github.com/Scienthusiasts/Machine-Learning
文章目录
1. 算法简介
如果要将当今的机器学习算法以统计学习的角度建模的话，一般可以划分为两个大的策略。一种属于判别式模型(discriminative models)，另一种是生成式模型(generative models)，本篇博客所要介绍的算法：贝叶斯分类器，或者说是朴素贝叶斯分类器，就属于生成式模型的一种。判别式与生成式这两类算法在以统计数学的角度的决策上存在着些许不同。
1.1 生成式模型 vs. 判别式模型
广义上，以统计学习的建模角度解释机器学习，我们可以给出以下的描述：
给定数据集D，D中的数据包含人为标注的M个类别，可以划分为M个子集。
D = { D 1 , D 2 , . . . , D M } D =\{ D_1, D_2, ...,D_M\} \\ D={D1,D2,...,DM}
其中，D中的每条数据包含有n个维度的特征：
X
∈
D
X
=
{
x
1
,
x
2
,
.
.
.
,
x
n
}
X \in D\\ X = \{x_1, x_2,...,x_n\}
X∈DX={x1,x2,...,xn}
判别式模型的决策过程
对于判别式模型而言。模型相当于从中学习某种条件概率函数。输入一个数据X, 通过模型习得的条件概率函数从输入映射得到一个输出，这个输出可以理解为后验概率P(Di|X)，即：输入一条数据，模型可以直接输出一个score，通过score的取值，来直接给出X属于哪一个类别(每个类别都有对应一个score范围)：
判
别
式
模
型
：
F
(
X
)
=
P
(
Y
∣
X
)
判别式模型：F(X)=P(Y|X)
判别式模型：F(X)=P(Y∣X)
其中的Y直接就是模型认为最有可能是X的类别。
相当于，判别式模型在决策过程中会将输入数据映射至一个相同的决策空间，并生成一个显式的决策边界，数据落入某个边界意味着数据就属于这个类别(如图一左所示)。
机器学习中有大量的算法思路均建立在判别式模型的基础上，其中就包括著名的决策树，线性回归模型，Logistic回归，前馈神经网络以及SVM等。
生成式模型的决策过程
生成式模型和判别式模型的不同在于，判别式模型在学习过程中对条件概率P(Di|X)建立函数模型，而生成式模型则是对联合概率P(Di,X)建立函数映射关系。
具体的差异在于：假设数据集中包含M个类别，生成式模型需要对每一个类别求取M个联合概率P(Di,X)，最终通过比较选取出这M个联合概率中最大的那个联合概率，其对应的参数Di就是算法认为的最有可能是X的类别：
生
成
式
模
型
：
F
(
X
)
=
a
r
g
m
a
x
D
i
[
P
(
D
1
,
X
)
,
P
(
D
2
,
X
)
,
.
.
.
,
P
(
D
M
,
X
)
]
生成式模型：F(X)=argmax_{D_i}[P(D_1,X), P(D_2,X),...,P(D_M,X)]
生成式模型：F(X)=argmaxDi[P(D1,X),P(D2,X),...,P(DM,X)]
相当于，模型会对数据集中的所有类别建模，即学习出每个类别的数据集子集的分布形式，建立Di和X的联合概率密度函数。在预测过程中，输入一条数据X，模型学习的函数f会将X映射至这M个决策空间中，求出联合分布P(Di,X)的概率，最终通过一一比对选出概率最大的概率对应的类别作为输出(如图一右所示)。
机器学习中生成式模型也有许多典型的代表，除了本次博客要介绍的朴素贝叶斯以外，常见的还有HMM隐马尔可夫模型，GMM高斯混合模型，限制波尔兹曼机等等。
再举个浅显易懂的例子：
假如我们现在有猫狗二分类数据集。对于判别式模型而言，模型会从数据集中学习出某些决策属性或参数，这些参数里耦合地包含了猫和狗的决策条件，在测试时输入一张图像，模型从图像中提取特征，通过这些特征判别图像是猫是狗；对于生成式模型而言，模型在学习过程中会直接学习出一个猫的模型，一个狗的模型(解耦合的)，将输入的图像提取特征，分别扔到这两个模型中，哪个概率大就属于哪个类别。
2. 算法思想
基于上文所述，朴素贝叶斯分类算法是一个生成式模型，其决策的数学原理依赖于历史上一个著名的统计学派的思想——贝叶斯学派。
著名的贝叶斯公式：
P
(
A
∣
B
)
=
P
(
B
,
A
)
P
(
B
)
=
P
(
B
∣
A
)
P
(
A
)
P
(
B
)
P\left(A \mid B\right)=\frac{P(B,A)}{P(B)}=\frac{P\left(B \mid A\right) P\left(A\right)}{P(B)}
P(A∣B)=P(B)P(B,A)=P(B)P(B∣A)P(A)
贝叶斯公式告诉我们，对于求解后验概率P(A|B), 可以将其转化为求解先验概率P(A)与似然概率P(B|A)的乘积，再除以一个"证据"因子P(B)。
贝叶斯分类器
利用贝叶斯公式对机器学习的过程建模，就是贝叶斯分类器的基本思想：
P
(
D
i
∣
X
)
=
P
(
X
∣
D
i
)
P
(
D
i
)
P
(
X
)
P\left(D_i \mid X\right)=\frac{P\left(X \mid D_i\right) P\left(D_i\right)}{P(X)}
P(Di∣X)=P(X)P(X∣Di)P(Di)
即，对于数据集中的某条输入样本X，机器学习的目标是获得给定X下属于某个类别Di的条件概率，即后验概率P(Di|X)。而贝叶斯分类器将这一后验概率转化为求取在某个类别Di下X样本出现的频率，即似然概率P(X|Di)，再乘上Di这一类别在总数据集中出现的频率，即先验概率P(Di),再除以样本X在数据集中出现的频率P(X)。
最后，通过比较不同类别下的P(Di|X),选取最大化后验概率作为模型输出。
通过观察我们发现，选取最大后验概率的过程中，表达式的分母均为P(X),对决策结果没有影响，因此可以省略。最终贝叶斯分类器的数学模型便是：
F
(
X
)
=
a
r
g
m
a
x
i
[
P
(
X
∣
D
1
)
P
(
D
1
)
,
P
(
X
∣
D
2
)
P
(
D
2
)
,
.
.
.
,
P
(
X
∣
D
M
)
P
(
D
M
)
]
F(X)=argmax_{i}[P(X|D_1)P(D_1),P(X|D_2)P(D_2),...,P(X|D_M)P(D_M)]
F(X)=argmaxi[P(X∣D1)P(D1),P(X∣D2)P(D2),...,P(X∣DM)P(DM)]
贝叶斯分类器理论上是可行的，不过一运用在现实生活中，就会产生不可预估的重重困难：
首先，对于输入样本X，通常会是一个高维的特征向量：
X
=
(
x
1
,
x
2
,
.
.
.
,
x
n
)
X = (x_1, x_2,...,x_n)
X=(x1,x2,...,xn)
这样一来，似然概率就是：
P
(
X
∣
D
i
)
=
P
(
x
1
,
x
2
,
.
.
.
,
x
n
∣
D
i
)
P(X|D_i) = P(x_1, x_2,...,x_n|D_i)
P(X∣Di)=P(x1,x2,...,xn∣Di)
事实上，其中的困难就来源于从训练集中找出与X一模一样的其他样本，即求取P(X|Di)是困难的。由排列组合公式不难得出，X的维度越大，X在D中出现的频率就越低，由于数据集总是有限的，因此假设新来一条样本X_new,训练集中往往找不到与之对应的样本，所以对于训练集而言，P(X_new|Di)的概率就为0。但这恰恰只能说明在训练集中样本X_new未被观察到，在现实世界中，“未被观测”与“出现概率为0”是两个完全不同的概念，两者不可一概而论。
如果这个问题无法解决，贝叶斯分类器就显得毫无意义，因为在这种情况下，求取似然概率和后验概率的难度是相当的,其中的困难都来源于稀缺的样本X：
后
验
概
率
：
P
(
D
i
∣
X
)
=
P
(
D
i
∣
x
1
,
x
2
,
.
.
.
,
x
n
)
似
然
概
率
：
P
(
X
∣
D
i
)
=
P
(
x
1
,
x
2
,
.
.
.
,
x
n
∣
D
i
)
后验概率：P(D_i|X) = P(D_i|x_1, x_2,...,x_n)\\ 似然概率：P(X|D_i) = P(x_1, x_2,...,x_n|D_i)
后验概率：P(Di∣X)=P(Di∣x1,x2,...,xn)似然概率：P(X∣Di)=P(x1,x2,...,xn∣Di)
kNN算法的统计学习诠释
(接下来是一个小插曲，有些跑题，但我觉得有必要在博客中记录自己的思考过程)：
这时候可能有人就会想了，既然求取两个概率的难度相当，何必大费周折，还把后验概率通过贝叶斯公式转化为求取似然概率和先验概率，这明明是雪上加霜好吧？
确实，我一开始也是这么想的，直接求取P(Di|X)不香吗，虽然X在训练集中几乎找不到与之对应的另一个样本，但是毛主席说过，没有条件创造条件也要上。
因此干脆放宽条件，何必找到和X一模一样的样本呢，把训练集中那些和X相似的样本当作X不就好了，具体要多相似可以根据训练集的规模而定。这样一来，训练集中的X的样本规模就有了保障，进一步的，求取P(Di|X)也便随之而出了。想到这我却突然眼前一亮，这个思路不就是kNN算法么！原来，kNN算法就是在求取后验概率P(Di|X)！，只不过这里X换成了和X相似的k个样本罢了。
【kNN算法在本专栏的第一篇博客已有解析，传送门：https://blog.youkuaiyun.com/SESESssss/article/details/120323905】
这样一来，以统计模型角度描述的kNN算法就是：
1.
设
距
离
度
量
函
数
为
d
(
⋅
)
2.
选
取
训
练
集
前
k
小
的
样
本
作
为
X
n
e
w
的
近
似
：
X
[
k
]
=
a
r
g
m
i
n
[
k
]
(
d
(
X
1
,
X
n
e
w
)
,
d
(
X
2
,
X
n
e
w
)
,
.
.
.
,
d
(
X
n
,
X
n
e
w
)
)
3.
则
后
验
概
率
P
(
D
i
∣
X
n
e
w
)
转
化
为
P
(
D
i
∣
X
[
k
]
)
\begin{aligned} &1.设距离度量函数为d(·)\\ &2.选取训练集前k小的样本作为X_{new}的近似：\\ &X_{[k]}=argmin_{[k]}(d(X_1,X_{new}), d(X_2,X_{new}),...,d(X_n,X_{new}))\\\\ &3.则后验概率P(D_i|X_{new}) 转化为 P(D_i|X_{[k]}) \end{aligned}
1.设距离度量函数为d(⋅)2.选取训练集前k小的样本作为Xnew的近似：X[k]=argmin[k](d(X1,Xnew),d(X2,Xnew),...,d(Xn,Xnew))3.则后验概率P(Di∣Xnew)转化为P(Di∣X[k])
这个思想我认为同样可以用在求取似然概率上。不过既然可以通过这种方法求取后验概率似乎就没必要求取似然概率了。
朴素贝叶斯分类器
回到正题，放宽条件这一个思路是正确的，除了放宽选择X的条件外还有一个方法，那就是
利用概率论中样本独立的条件概率公式进行转化,我们假设样本X中的每一个维度相互之间是独立的随机变量，则有：
P
(
D
i
∣
x
1
,
x
2
,
.
.
.
,
x
n
)
=
P
(
D
i
∣
x
1
)
⋅
P
(
D
i
∣
x
2
)
⋅
⋅
⋅
⋅
P
(
D
i
∣
x
n
)
=
∏
j
=
1
n
P
(
x
j
∣
D
i
)
P(D_i|x_1,x_2,...,x_n) = P(D_i|x_1)·P(D_i|x_2)····P(D_i|x_n)\\ =\prod_{j=1}^{n} P\left(x_{j} \mid D_i\right)
P(Di∣x1,x2,...,xn)=P(Di∣x1)⋅P(Di∣x2)⋅⋅⋅⋅P(Di∣xn)=j=1∏nP(xj∣Di)
这样一来，即使P(Di|x1,x2,…,xn)在训练集中的存在条件过于苛刻，P(Di|xj)也相对容易求取。这时候，我们将后验概率转化为求取似然概率，就相对容易的多，贝叶斯准则也有了它的用武之地，这时候由于多了一个前提假设(样本不同维度之间的特征相互独立)，朴素贝叶斯(naive bayes)也因此得名。
换言之，朴素贝叶斯算法为了简化求解联合概率，假设每个属性独立地对分类结果产生影响。这时候的分类规则便是：
F
(
X
)
=
arg
max
i
P
(
D
i
)
∏
i
=
1
n
P
(
x
i
∣
D
i
)
F(X)=\underset{i}{\arg \max } P(D_i) \prod_{i=1}^{n} P\left(x_{i} \mid D_i\right)
F(X)=iargmaxP(Di)i=1∏nP(xi∣Di)
3. 算法流程
3.1 算法的一般训练流程
训练过程无非就是计算P(xj|Di)和P(Di)，其流程如下：
- 读取训练集D和所属类别标签；
- 将数据集根据标签划分为若干子数据集；
- 遍历所有子数据集Di，计算先验概率P(Di)；
- 在Di中遍历数据集所有维度，穷举每个维度可能的取值，计算每个属性的似然概率P(xj|Di)；
- 将上述计算结果以某种数据结构保存为模型权重。
伪代码：
3.2 算法的一般推理流程
对于朴素贝叶斯算法，其预测过程就基于part2给出的公式：
- 读取训练得到的模型(其实就是一堆已经计算好的概率)
- 遍历所有类别下对应的模型；
- 将X基于子数据集Di的联合条件概率拆分成每个属性的条件概率的乘积，乘积的结果作为似然概率；
- 将似然概率P(X|Di)与先验概率P(Di)相乘得到联合概率P(X, Di)，由于证据因子P(X)对于所有子数据集都是相同的，因此单纯进行比较的情况下可以忽略；
- 最后，求取似然概率最大子数据集作为预测结果。
在这段描述中，可以看到朴素贝叶斯算法具有鲜明的生成式模型的特征。
伪代码：
4. 三种朴素贝叶斯模型
在3.1part中我们给出了朴素贝叶斯算法的一般训练过程，其中在计算似然概率P(xj|Di)的部分我们只是给了一种较为简洁直观的计算方法，即将属性xj出现的频率除以Di数据集的总数，得到的比例就作为似然概率。
这种统计方法在统计学中叫做伯努利实验，伯努利实验准确的前提要求实验次数足够多，换言之就是样本数据足够大，满足大数定律。但是在实际情况下，如果数据集的属性一多起来，相应的每一种属性出现的频率就会随之减少，这样一来对于数据集的需求也就更多，因此单纯的以出现频率作为似然概率并不一定适合所有的数据集。
因此，基于数据本身具有的特征，朴素贝叶斯算法还可以再细分为三种类型，其算法的差异就主要体现在如何计算似然概率这一点上。
4.1 伯努利朴素贝叶斯
基于伯努利分布的朴素贝叶斯算法实际上就是基于3.1part给出的计算方法，我们都知道伯努利实验，一个最著名的例子就是计算抛硬币出现正反面的概率。实验中的样本只有两个非黑即白的结果，因此我们也说抛硬币的结果服从二项分布，对于属性服从二项分布的数据(一般是二值化的离散变量)，我们可以使用伯努利朴素贝叶斯来计算似然概率：
P
(
x
j
=
1
∣
D
i
)
=
∣
D
i
,
j
=
1
∣
∣
D
i
∣
P
(
x
j
=
0
∣
D
i
)
=
1
−
P
(
x
j
=
1
∣
D
i
)
P\left(\mathrm{x}_{j}=1 \mid D_i\right)=\frac{\left|D_{i, j}=1\right|}{\left|D_{i}\right|}\\ P\left(\mathrm{x}_{j}=0 \mid D_i\right)=1 - P\left(\mathrm{x}_{j}=1 \mid D_i\right)
P(xj=1∣Di)=∣Di∣∣Di,j=1∣P(xj=0∣Di)=1−P(xj=1∣Di)
拉普拉斯修正(Laplacian smoothing)
当然，无论是何种贝叶斯算法，仍然不可能完全规避测试集中出现训练集没出现的属性，就如part2中所言，“未观测到”与“概率为0”不可一概而论，因此现实在计算时常常要加入拉普拉斯修正，拉普拉斯修正本质上是引入了一种无信息的均匀先验分布，赋予未观测事件一个小概率：
P
^
(
D
i
)
=
∣
D
i
∣
+
1
∣
D
∣
+
N
P
^
(
x
j
∣
D
i
)
=
∣
D
i
,
x
j
∣
+
1
∣
D
i
∣
+
N
j
\begin{aligned} \hat{P}(D_i) &=\frac{\left|D_{i}\right|+1}{|D|+N} \\ \hat{P}\left(x_{j} \mid D_i\right) &=\frac{\left|D_{i, x_{j}}\right|+1}{\left|D_{i}\right|+N_{j}} \end{aligned}
P^(Di)P^(xj∣Di)=∣D∣+N∣Di∣+1=∣Di∣+Nj∣∣Di,xj∣∣+1
其中，N表示训练集D中的类别数，Nj表示数据集第j维度可能出现的取值数。拉普拉斯修正能够防止概率为0的情况出现，对于一条未见的属性，相应的似然概率就是1/(Di+Nj)
4.2 多元伯努利朴素贝叶斯
多元伯努利试验和伯努利试验的差别在于，一个基于二项分布，一个基于多项分布，仅此而已。
基于多元伯努利朴素贝叶斯的似然概率公式是伯努利朴素贝叶斯一般化形式：
P
(
x
j
=
k
∣
D
i
)
=
∣
D
i
,
j
=
k
∣
∣
D
i
∣
P\left(\mathrm{x}_{j}=k \mid D_i\right)=\frac{\left|D_{i, j}=k\right|}{\left|D_{i}\right|}\\
P(xj=k∣Di)=∣Di∣∣Di,j=k∣
代码实战：MNIST手写数字识别
对于图像而言，我们可以将其展开成一维向量，这样一来，图像的每一个像素就作为一个特征，像素的灰度值就作为特征属性可能的取值。对于伯努利朴素贝叶斯，我们希望数据的属性只有两个取值，满足这个前提只需要将图像二值化便能实现。下面提供代码的具体细节：
import numpy as np
import pickle
from collections import Counter
class naiveBayes:
def __init__(self, X, y):
self.X = X
self.y = y
'''读取权重'''
def loadWeight(self, path):
file = open(path, 'rb')
weight = pickle.load(file)
print(weight)
self.likelihood = weight[:-1]
self.cls_num = weight[-1]
'''伯努利朴素贝叶斯(0,1);多元伯努利朴素贝叶斯(0,1,...,n)'''
'''计算似然概率'''
# 适用于二值化图像(离散值处理)
def calcLikelihood(self, N):
cls_num = []
total_num = self.X.shape[0]
# 统计数据集中的所有类别
classes = set(self.y)
# 将同类的数据划分到一起
division = [self.X[np.where(self.y==i)] for i in classes]
# 计算先验概率 = 该类别数 / 数据集总数
self.prior = [type.shape[0] / total_num for type in division]
# 计算似然概率：
likelihood = np.zeros((len(classes), self.X.shape[1]))
# 转化为列表方便添加不同类型的元素(字典)
likelihood = likelihood.tolist()
# 计算似然概率
for i, type in enumerate(division):
for j in range(self.X.shape[1]):
# 统计属性出现次数
tmp_dict = dict(Counter(type[:,j]))
# 似然概率 = 属性出现次数 / 数据集这个类别的总数
for key in tmp_dict.keys():
tmp_dict[key] = (tmp_dict[key] + 1) / (type.shape[0] + N)
likelihood[i][j] = tmp_dict
cls_num.append(type.shape[0])
self.likelihood = likelihood
self.cls_num = cls_num
print(cls_num)
# 保存权重
file = open('weight.txt', 'wb')
pickle.dump(self.likelihood + [self.cls_num], file)
'''计算后验概率'''
# 适用于二值化图像(离散值处理)
def calcPosterior(self, X_test, N):
cls_num = len(self.likelihood)
sum = np.ones(cls_num)
# 逐维度计算似然概率，条件概率=似然概率的乘积(每个维度独立的假设下)
for i in range(cls_num):
for j in range(X_test.shape[0]):
if X_test[j] in self.likelihood[i][j].keys():
# 取对数运算防止下溢出
sum[i] += np.log(self.likelihood[i][j][X_test[j]])
# sum[i] *= self.likelihood[i][j][X_test[j]]
else:
# laplacian修正，防止概率为0
sum[i] += np.log(1 / (self.cls_num[i] + N))
# sum[i] *= 1e-3
return np.argmax(sum)
值得注意的是，在计算联合概率P(Di,X)时，本应该将其转化为P(Di|X)·P(Di)。但最后还是决定在计算时舍去先验概率P(Di)，除了简化运算之外，一个很重要的原因是：先验概率反映了样本不同的类别出现的频率。但是对于手写数字而言，日常生活中0-9出现的几率理应是均等的，因此省略(在接下来的例子中，先验概率均不参与计算，特此说明)。
main函数：
metrics是自己实现的用于结果评估的相关库，具体实现已在第一篇博客kNN给出，传送：
import numpy as np
from naiveBayes import naiveBayes
from tqdm import trange # 进度条库
import sys;sys.path.append('../metrics')
from metrics import metrics
datapath = 'MNIST'
X_train = np.load('../datasets/%s/train_sets.npy' % datapath).reshape(-1,784)
y_train = np.load('../datasets/%s/train_labels.npy' % datapath)
X_test = np.load('../datasets/%s/valid_sets.npy' % datapath).reshape(-1,784)
y_test = np.load('../datasets/%s/valid_labels.npy' % datapath)
# 二值化
X_train[X_train>0]=1
X_test[X_test>0]=1
NB = naiveBayes(X_train, y_train)
# 模型训练:
# NB.calcLikelihood(2)
# 导入"权重":
NB.loadWeight('weight.txt')
# 计算测试集精度：
pred = []
sum = 0
for i in trange(10000):
pred.append(NB.calcPosterior(X_test[i,:], 2))
sum += pred[-1] == y_test[i]
print(sum / 10000)
np.save('pred.npy',np.array(pred))
pred = np.load('pred.npy')
# 绘制混淆矩阵:
label = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']
metrics.confusion_matrix_vis(y_test, pred, label)
metrics.precision_recall(y_test, pred, label)
伯努利朴素贝叶斯混淆矩阵可视化与算法查准率，查全率对比：
在测试集的精度：84.15%
我们同样可以在MNIST数据集上测试多元伯努利朴素贝叶斯算法，这时候甚至不需要将图像二值化处理。
多元伯努利朴素贝叶斯混淆矩阵可视化与算法查准率，查全率对比：
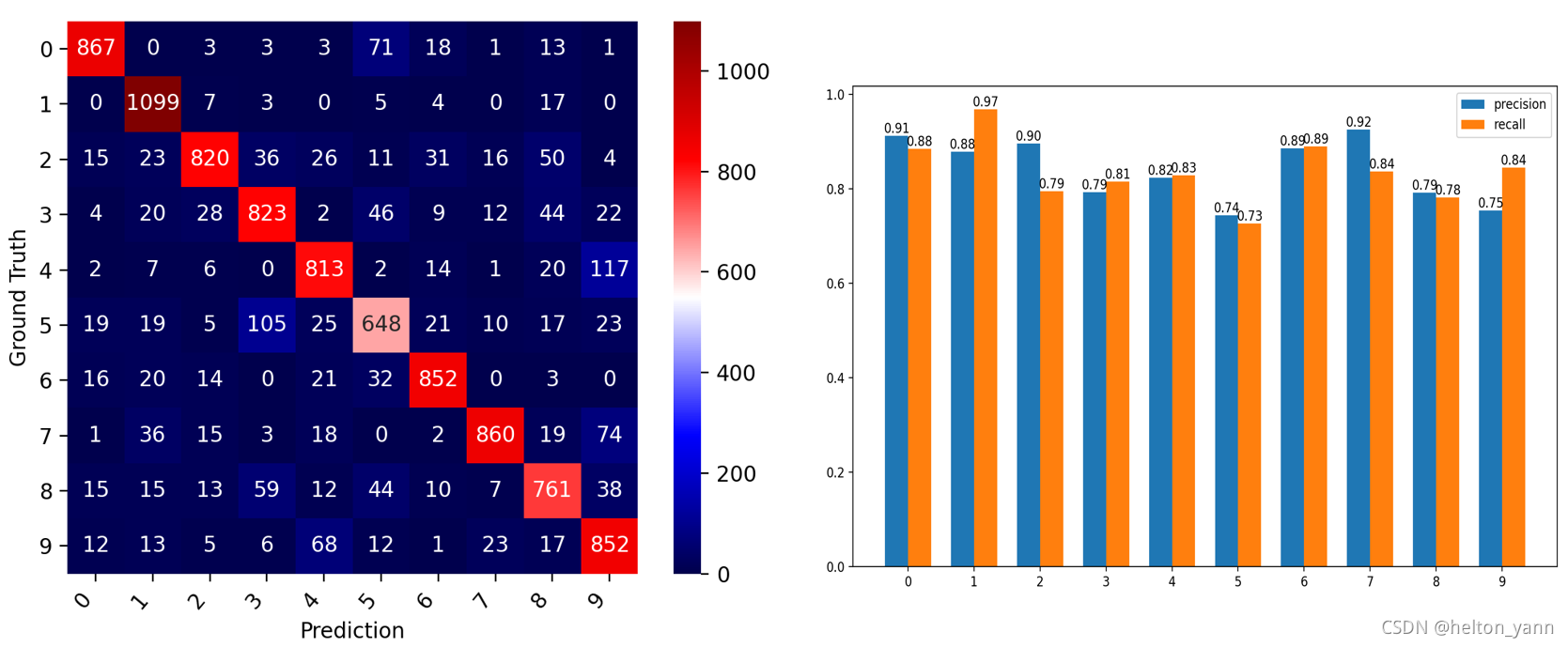
在测试集的精度：83.95%
客观上来说，原始图像包含的信息会远多于二值化图像的信息，因此理论上应该是原始图像的预测精度优于二值化图像的预测精度。但是测试结果显示算法在二值化图像测试精度(84.15%)要稍微优于原始的灰度阶为(0-255)的图像(83.95%)。一个主要的原因还是在似然概率的计算误差上。就如前文所说的，数据的属性一多，相应的就需要更多的数据参与统计来缓解小规模伯努利实验本身的误差(如果从模型拟合的角度，我的理解是，属性过多导致的似然概率估计误差属于朴素贝叶斯算法的一种过拟合原因，缓解过拟合的方法是适当减小样本属性的取值，或者是增加样本数量)。不过，模型的属性过多往往还有另一个原因，有可能是属性本身是连续的。因此在贝叶斯分类算法上，对于连续性较强的属性我们往往有另一种统计似然概率的方法：高斯朴素贝叶斯。
4.3 高斯朴素贝叶斯
对于连续性属性而言，将其离散化后，我们一般很难观测到样本全部的取值，这也是多元伯努利朴素贝叶斯的误差来源。一般情况下，依据中心极限定理，在训练样本数量足够时，我们可以假定连续性属性服从高斯分布，其均值为μ，标准差为σ，μ和σ可以通过估计训练样本中该属性的均值和标准差得到。
这样一来，基于高斯分布的似然概率函数就是(避免混淆，数据集用C表示)：
P
(
x
j
∣
C
i
)
=
N
(
x
j
∣
μ
j
,
σ
j
2
)
=
1
2
π
σ
exp
−
(
x
j
−
μ
j
)
2
2
σ
j
2
其
中
：
μ
j
=
E
(
C
i
,
j
)
，
σ
j
2
=
D
(
C
i
,
j
)
P\left(\mathrm{x}_{j} \mid C_i\right)=N\left(x_j \mid \mu_j, \sigma^{2}_j\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp -\frac{(x_j-\mu_j)^{2}}{2 \sigma^{2}_j}\\ 其中：μ_j = E(C_{i,j})， σ_j^2=D(C_{i,j})
P(xj∣Ci)=N(xj∣μj,σj2)=2πσ1exp−2σj2(xj−μj)2其中：μj=E(Ci,j)，σj2=D(Ci,j)
值得注意的是，高斯分布的函数值并不表示概率值，只能作为一种频数表示，但是概率-频数这两个属性是呈单调正相关的，因此对于单纯比较而言，频数可以取代真实的概率。
代码实战：MNIST手写数字识别
高斯朴素贝叶斯将逐一统计每个灰度值出现的频率转为只需计算每个维度的均值和方差，一定程度上也可以起到压缩模型的效果：
import numpy as np
import pickle
from collections import Counter
class naiveBayes:
def __init__(self, X, y):
self.X = X
self.y = y
self.cls_num = []
'''读取权重'''
def loadWeight(self, path, cls_num):
file = open(path, 'rb')
weight = pickle.load(file)
if len(weight) == cls_num:
self.likelihood = weight
else:
self.likelihood = weight[:-1]
self.cls_num = weight[-1]
'''保存权重'''
def saveWeight(self, path):
file = open(path, 'wb')
if len(self.cls_num) == 0:
pickle.dump(self.likelihood, file)
else:
pickle.dump(self.likelihood + [self.cls_num], file)
'''高斯朴素贝叶斯'''
# 适用于一般图像(连续值处理, 使用正态分布)
def calcLikelihood(self):
total_num = self.X.shape[0]
# 统计数据集中的所有类别
classes = set(self.y)
# 将同类的数据划分到一起
division = [self.X[np.where(self.y==i)] for i in classes]
# 计算先验概率 = 该类别数 / 数据集总数
self.prior = [type.shape[0] / total_num for type in division]
# 计算似然概率：
likelihood = np.zeros((len(classes), self.X.shape[1]))
# 转化为列表方便添加不同类型的元素(字典)
likelihood = likelihood.tolist()
# 计算似然概率
for i, type in enumerate(division):
for j in range(self.X.shape[1]):
μ = np.mean(type[:,j])
σ = np.var(type[:,j])
likelihood[i][j] = [μ, σ]
self.likelihood = likelihood
# 假设连续值服从正态分布
def gaussian_distribution(self, x, μ, σ):
σ += 2e-1 # 平滑
return np.exp(-(x - μ)*(x - μ) / (2 * σ)) / (np.sqrt(2 * np.pi * σ) )
def calcPosterior(self, X_test):
cls_num = len(self.likelihood)
sum = np.zeros(cls_num)
for i in range(cls_num):
for j in range(X_test.shape[0]):
μ = self.likelihood[i][j][0]
σ = self.likelihood[i][j][1]
if X_test[j] == 0 and σ == 0:
sum[i] -= 1 # 防止加上一个过大的值
else:
sum[i] += np.log(self.gaussian_distribution(X_test[j], μ, σ))
return np.argmax(sum)
main函数：
import numpy as np
from naiveBayes import naiveBayes
import matplotlib.pyplot as plt
from tqdm import trange # 进度条库
import sys;sys.path.append('../metrics')
from metrics import metrics
datapath = 'MNIST'
X_train = np.load('../datasets/%s/train_sets.npy' % datapath).reshape(-1,784)
y_train = np.load('../datasets/%s/train_labels.npy' % datapath)
X_test = np.load('../datasets/%s/valid_sets.npy' % datapath).reshape(-1,784)
y_test = np.load('../datasets/%s/valid_labels.npy' % datapath)
# 取对数使得数据近似为高斯分布
# X_train = np.log(X_train.astype(np.float) + 1)
# X_test = np.log(X_test.astype(np.float) + 1)
# 二值化
# X_train[X_train>0]=1
# X_test[X_test>0]=1
# 数据集可视化
for i in range(32):
plt.subplot(4, 8, i+1)
img = X_train[i,:].reshape(28, 28)
plt.imshow(img)
plt.title(y_train[i])
plt.axis("off")
plt.subplots_adjust(hspace = 0.3) # 微调行间距
plt.show()
NB = naiveBayes(X_train, y_train)
# 模型训练:
NB.calcLikelihood()
NB.saveWeight("weight_gau.txt")
# 导入"权重":
NB.loadWeight('weight_gau.txt',10)
# 计算测试集精度：
pred = []
sum = 0
for i in trange(1000):
pred.append(NB.calcPosterior(X_test[i,:]))
sum += pred[-1] == y_test[i]
print(sum / 1000)
np.save('pred_gau.npy',np.array(pred))
不过，使用高斯函数计算似然概率虽然解决了未观测数据的问题，但同时又引入了一个问题，那就是当训练样本的属性取值较少或单一时，会导致频数过大或除以0的现象，最终影响分类效果。因此为了避免除0以及函数"尖峰"过于突出，本人在计算时引入了”平滑因子“，对于方差σ加上一个较小的值(1e-1)。以此同时，对于单样本的情况(方差为0)，只包括平滑因子会导致频数过大，因此手动给予单样本维度一个先验的高斯函数值(e^-5)【事实上，这些超参数都是基于实验试出来的在测试集上效果最好的值 🤔,并且博主通过实验发现超参的取值和数据的分布有很大关系。至于为什么取这些值效果会好博主本人也不是很清楚。。这里先打一个小疑问，若有大佬能在评论区解答，本人感激不尽】
然而，很遗憾的是，即使加入了上面的trick，最终在测试集上的准确率却仅达到了0.767%，甚至劣于伯努利朴素贝叶斯😢。哈哈，别忘了，这是因为我们还忽略了一个高斯朴素贝叶斯的一个很重要前提假设：
D
i
,
j
∼
N
(
μ
i
,
j
,
σ
i
,
j
)
D_{i,j} \sim N(μ_{i,j}, σ_{i,j})
Di,j∼N(μi,j,σi,j)
简单来说，我们假设属性xj是服从高斯分布的，然而在样本不足的情况下，这个假设并不严格成立：我们可以show一下样本属性的分布看看:
def show_distribution():
X_train = np.load('../datasets/MNIST/train_sets.npy').reshape(-1)
count = np.zeros(256)
for i in X_train:
count[i] += 1
axis = np.arange(256)
plt.bar(axis, count, width=1)
plt.xlabel("grey scale")
plt.ylabel("frequency")
plt.show()
一般情况下，不满足正态分布的数据通常是偏态分布，它们通常长这样：
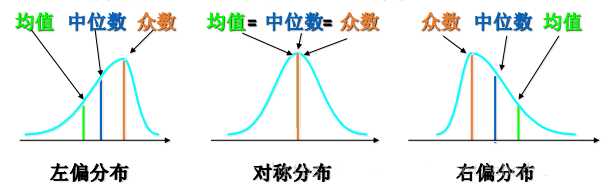
像偏态分布，它们都有一个先增大再减小的趋势，针对右偏分布，我们可以取对数或者开平方根，这是因为对数曲线或者平方根曲线都有一个特点：它们的变化率是逐渐减小的，因此能够把小数值扩展，大数值压缩(数字图像处理中的灰度变换函数也是同样的原理，所以说知识是相通的)把右偏分布转化为正态分布，对于左偏分布，一般可以取指数型曲线变换或者取反转化为右偏分布再做处理。
然而，仔细观察我们的数据，它既不是左偏分布也不是右偏分布，所以上述的方法似乎无效。。。吗
事实上，本人将数据取log变换后，精度确确实实提升了百分之十几(83%)(平滑因子=0.02，高斯函数先验值=1/e)，我们可以show一下对数变换后的灰度阶分布(最后又映射回0,255)：
可以看出虽然说分布仍然不像正态分布，但至少可以明显看出log变换后左边的高峰向右偏移了。【至于说为什么取log后仍然可以显著提升精度，这里也打个小疑问🤔】
基于似然概率最大化的模型可视化
由于朴素贝叶斯算法是一个生成式模型，因此在训练过程中算法会对每一个类别下的数据的联合概率P(xj，Di)建模，省略先验概率的条件下，就是似然概率P(xj|Di)。因此我们可以反向操作，选择属性xj以最大化似然概率P(xj|Di)，基于此我们可以生成一条全新的样本，这个样本即"模型认为的最有可能属于该类别"的模样。
import numpy as np
import matplotlib.pyplot as plt
import pickle
'''基于高斯朴素贝叶斯的似然概率最大化'''
def show_ber(likelihood):
for image in likelihood:
img = np.zeros(len(image))
for i in range(len(image)):
# 遍历所有属性
for attr in image[i].keys():
# 所有属性以概率值加权和作为灰度值:
img[i] += attr * image[i][attr]
plt.imshow(img.reshape(28, 28))
plt.show()
'''基于高斯朴素贝叶斯的似然概率最大化'''
def show_gau(likelihood):
for image in likelihood:
img = np.zeros(len(image))
for i in range(len(image)):
img[i] = image[i][0]
plt.imshow(img.reshape(28, 28))
plt.show()
# 可视化贝叶斯似然概率模型
file = open('weight_gau.txt', 'rb')
likelihood = pickle.load(file)
show_gau(likelihood)
基于伯努利分布的似然概率模型最大化：
基于高斯分布的似然概率模型最大化：
事实上，上述的例子都是基于计算机视觉图像识别任务，然而朴素贝叶斯算法最成功的的应用其实是在文本分类任务上。在约20年前，朴素贝叶斯算法就曾被认为是处理垃圾邮件分类的最佳选择。值得一提的是，对于自然语言处理一类的任务，我比较常用的是朴素贝叶斯的第三种类型，多项式朴素贝叶斯
4.4 多项式朴素贝叶斯
在机器学习当中，自然语言处理任务有别于计算机视觉任务，往往情况更为复杂且一般。自然语言不像图像，一张图像的尺寸往往是规范且确定的，然而句子与句子之间却是长短不一的，如果以图像的思路进行处理，必然会造成短句子某些维度的缺失。同时，由于自然语言拥有的词汇量往往很大，并且词汇无法作为连续值进行处理，这对于似然概率的计算必然会更加困难(需要更大的样本量)。这时候要考虑多项式朴素贝叶斯。
多项式朴素贝叶斯的似然概率计算依赖于多项分布。多项分布实则就是二项分布的推广，具体而言，如果二项分布是抛硬币，那么多项分布就是掷骰子。它研究的问题是：如果掷n次骰子，那么点数1-6出现次数为(n1,n2,n3,n4,n5,n6)的概率是多少(和-6出现的先后顺序无关),其中xi的总和为n。
多项分布的概率公式为：
P
(
x
1
,
x
2
,
.
.
.
,
x
k
)
=
n
!
∏
j
=
1
k
p
j
n
j
n
j
!
,
∑
j
=
1
k
n
j
=
n
P(x_1,x_2,...,x_k)=n ! \prod_{j=1}^{k} \frac{p_{j}^{n_{j}}}{n_{j} !} \quad, \sum_{j=1}^{k} n_{j}=n
P(x1,x2,...,xk)=n!j=1∏knj!pjnj,j=1∑knj=n
对于似然概率的计算，就是：
P
(
x
1
,
x
2
,
.
.
.
,
x
k
∣
D
i
)
=
n
!
∏
j
=
1
k
p
i
,
j
n
j
n
j
!
,
∑
j
=
1
k
n
j
=
n
P(x_1,x_2,...,x_k|D_i)=n ! \prod_{j=1}^{k} \frac{p_{i,j}^{n_{j}}}{n_{j} !} \quad, \sum_{j=1}^{k} n_{j}=n
P(x1,x2,...,xk∣Di)=n!j=1∏knj!pi,jnj,j=1∑knj=n
其中，pij表示属性xj在Di子集中出现的频率。
具体到文本分类问题上，一般情况下，我们会基于一个词袋模型(Bag of Words)统计出一个词频向量，里面包含所有在训练集中出现过词语的次数，用于计算pij，公式中的n就可以特指单词总数。除此之外，为了简化计算，对于文本分类而言，我们一般不考虑一段话的词序，而将某些词语出现的频率作为判断依据。即“I Love You”和“You Love I”是毫无差别的，这对于多项分布而言也是如此。
在公式中，n和nj通常是定值，即和所属类别Di无关。因此在求解比对最大似然概率时，这两个变量就相当于常数，可以被忽略。
简化后的似然概率公式：
P
(
x
1
,
x
2
,
.
.
.
,
x
k
∣
D
i
)
=
∏
j
=
1
k
p
i
,
j
n
j
P(x_1,x_2,...,x_k|D_i)=\prod_{j=1}^{k} p_{i,j}^{n_j} \quad
P(x1,x2,...,xk∣Di)=j=1∏kpi,jnj
取对数似然就是
P
(
x
1
,
x
2
,
.
.
.
,
x
k
∣
D
i
)
=
∑
j
=
1
k
n
j
⋅
l
o
g
(
p
i
,
j
)
P(x_1,x_2,...,x_k|D_i)=\sum_{j=1}^{k} n_j·log(p_{i,j}) \quad
P(x1,x2,...,xk∣Di)=j=1∑knj⋅log(pi,j)
对于概率pij，由于多项式分布是伯努利分布的推广，因此计算方式同伯努利朴素贝叶斯，同样基于伯努利试验：
p
i
,
j
=
∣
D
i
=
x
j
∣
∣
D
i
∣
p_{i,j}=\frac{\left|D_{i}=x_j\right|}{\left|D_{i}\right|}\\
pi,j=∣Di∣∣Di=xj∣
其中Di表示Di中的总词数，Di=xj表示词xj在Di中出现的总次数。
代码实战：imdb影评数据集分类
数据集简介
IMDB数据集来源于著名电影资讯分享网站IMDB的影评内容(英语)。这是著名的用于情感二分类的数据集，包含了对于电影两级分化的评价(好评/差评)。数据集总共包含50000条电影评论文本，其中25000条用于训练，25000条用于测试，训练和测试中的好评/差评文本各半。
数据集下载链接：https://www.kaggle.com/stefanoleone992/imdb-extensive-dataset
数据集文件结构：
imdb/:.
├─test
│ ├─neg
│ └─pos
└─train
├─neg
├─pos
└─unsup
其中unsub代表未打标签的文本，本次实验不涉及。其他的文件夹如/neg或/pos代表负面/正面评价的文本。
文本数据预处理：
将文本转化为计算机可处理的数据格式可比图像要复杂得多。一般来说，对于一段文本，我们首先需要将文本分词处理。去除掉对预测结果影响不大的标点符号，并转化为全小写(BoW里的单词都是小写)，同时考虑到方便读取的因素，在保存时将同一个类别的文本保存到一个二进制文件中：
def read_datasets():
path = 'test/neg/'
datasets = []
for file_path in os.listdir(path):
file = open(path + file_path, encoding='UTF-8')
comment = file.readlines()[0]
# 预处理:
comment = comment.replace('<br />', ' ')
# 定义待去除的标点符号集(正则化表达式)
punc = '[’!"#$%&\'()*+,-./:;<=>?@[\\]^_`{|}~\n。！，]+'
# 去除标点符号,并转化为小写
comment = re.sub(punc,'',comment).lower()
datasets.append(comment.split(' '))
# 以二进制文件保存
file = open('test_neg.txt', 'wb')
pickle.dump(datasets, file)
对于一段文本：
Story of a man: who has unnatural feelings for a pig.
去除标点，转小写，分词，转化为列表：
[‘story’, ‘of’, ‘a’, ‘man’, ‘who’, ‘has’, ‘unnatural’, ‘feelings’, ‘for’, ‘a’, ‘pig’]
imdb数据集还算人性化，在数据文件中提供了词袋模型imdb.vocab,里面包含了80000余条数据集中可能出现的词汇(甚至还包含某些标点)
‘the’, ‘and’, ‘a’, ‘of’, ‘to’, ‘is’, ‘it’, ‘in’, ‘i’, ‘this’, ‘that’, ‘was’, ‘as’, ‘for’, ‘with’, ‘movie’, ‘but’, ‘film’, ‘on’, ‘not’, ‘you’, ‘he’, ‘are’, ‘his’, ‘have’, ‘be’, ‘one’, ‘!’, ‘all’, ‘at’, ‘by’, ‘an’, ‘who’, ‘they’, ‘from’, ‘so’, ‘like’, ‘there’, ‘her’, ‘or’, ‘just’, ‘about’, ‘if’, ‘has’, ‘out’, ‘what’, ‘?’, ‘some’, ‘good’, ‘more’, ‘when’, ‘she’, ‘very’, ‘even’, ‘my’, ‘no’, ‘up’, ‘time’, … …
根据词袋模型，我们可以统计出每个类别下的长度为80000的词频向量，这个词频向量就用来当做算法训练得到的似然概率模型：
'''多项式朴素贝叶斯'''
'''计算似然概率(适用于文本分类)'''
# 统计某类别下的词频
def calcWordFreq(self, bow, texts):
hist = np.zeros(len(bow))
for i, text in enumerate(texts):
for word in text:
if word in bow:
hist[bow.index(word)] += 1
print(i)
return hist
词频向量可视化：
多项式贝叶斯分类器：
import numpy as np
import pickle
from collections import Counter
class naiveBayes:
def __init__(self, X, y):
self.X = X
self.y = y
self.cls_num = []
'''读取权重'''
def loadWeight(self, path, cls_num):
file = open(path, 'rb')
weight = pickle.load(file)
if len(weight) == cls_num:
self.likelihood = weight
else:
self.likelihood = weight[:-1]
self.cls_num = weight[-1]
'''保存权重'''
def saveWeight(self, path):
file = open(path, 'wb')
if len(self.cls_num) == 0:
pickle.dump(self.likelihood, file)
else:
pickle.dump(self.likelihood + [self.cls_num], file)
'''多项式朴素贝叶斯'''
'''计算似然概率(适用于文本分类)'''
# 统计某类别下的词频
def calcWordFreq(self, bow, texts):
hist = np.zeros(len(bow))
for i, text in enumerate(texts):
for word in text:
if word in bow:
hist[bow.index(word)] += 1
print(i)
return hist
'''计算后验概率(适用于文本分类 no unique/ unique)'''
def calcPosterior(self, X, freq_vec, bow):
sum = np.zeros(freq_vec.shape[0])
# 统计不同类别下的后验概率：
for i in range(freq_vec.shape[0]):
total_num = np.sum(freq_vec[i,:])
X_cnt = dict(Counter(X))
for word in X_cnt.keys():
# 如果词语在词袋中:
if word in bow:
# 统计词频
frec = freq_vec[i, bow.index(word)] / total_num
if frec != 0:
sum[i] += X_cnt[word] * np.log(frec)
# 如果词频向量中该词语=0
else:
# 平滑一个小概率，概率不能为 0
sum[i] += np.log(1 / total_num)
# 如果词语不在词袋中:
else:
# 平滑一个小概率，概率不能为 0
sum[i] += np.log(1 / total_num)
return np.argmax(sum)
main函数
import numpy as np
import pickle
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler # 标准归一化
from naiveBayes import naiveBayes
from tqdm import trange # 进度条库
file = open('imdb_cut/train_neg_nounique.txt', 'rb');X_train_neg = pickle.load(file)
file = open('imdb_cut/train_pos_nounique.txt', 'rb');X_train_pos = pickle.load(file)
file = open('imdb_cut/test_neg_nounique.txt', 'rb');X_test_neg = pickle.load(file)
file = open('imdb_cut/test_pos_nounique.txt', 'rb');X_test_pos = pickle.load(file)
file = open('imdb_cut/bag.txt', 'rb');bow = pickle.load(file)
# 模型训练:
NB = naiveBayes(X_train_neg, X_train_neg)
# 统计正负样本的词频：
# neg_hist = NB.calcWordFreq(bow, X_train_neg)
# pos_hist = NB.calcWordFreq(bow, X_train_pos)
# np.save('neg_hist.npy', neg_hist)
# np.save('pos_hist.npy', pos_hist)
# 导入训练好的词频:
neg_hist = np.load('imdb_cut/neg_hist.npy').reshape(1,-1)
pos_hist = np.load('imdb_cut/pos_hist.npy').reshape(1,-1)
freq_vec = np.concatenate((neg_hist, pos_hist), axis=0)
# 词频可视化
plt.subplot(211)
plt.plot(neg_hist[0])
plt.ylim(0,6000)
plt.xlabel('neg Words index')
plt.ylabel('frequency')
plt.subplot(212)
plt.plot(pos_hist[0])
plt.ylim(0,6000)
plt.xlabel('pos Words index')
plt.ylabel('frequency')
plt.legend()
plt.show()
# 评估测试集:
sum_pos = []
sum_neg = []
for i in trange(12500):
pred = NB.calcPosterior(X_test_pos[i], freq_vec, bow) == 1
# print(i, pred)
sum_pos.append(pred)
for i in trange(12500):
pred = NB.calcPosterior(X_test_neg[i], freq_vec, bow) == 0
# print(i, pred)
sum_neg.append(pred)
# pred = np.load('naive_bayes/imdb_cut')
print(np.sum(sum_pos) / 12500)
print(np.sum(sum_neg) / 12500)
# 保存测试结果:
np.save('pred_pos.npy', np.array(sum_pos))
np.save('pred_neg.npy', np.array(sum_neg))
评估模块:
import numpy as np
import sys;sys.path.append('../metrics')
from metrics import metrics
pred_pos = np.load('imdb_nounique/pred_pos.npy')
pred_neg = np.load('imdb_nounique/pred_neg.npy')
pred_all = np.concatenate([pred_pos, ~pred_neg])
y = np.concatenate([np.ones(pred_pos.shape[0]), np.zeros(pred_neg.shape[0])])
pos_acc = sum(pred_pos) / pred_pos.shape[0]
neg_acc = sum(pred_neg) / pred_neg.shape[0]
print('pos acc:%f, neg acc:%f, total acc:%f' % (pos_acc, neg_acc, (pos_acc + neg_acc) / 2))
# 绘制混淆矩阵:
label = np.arange(2)
metrics.confusion_matrix_vis(y, pred_all, label)
metrics.precision_recall(y, pred_all, ['neg','pos'])
混淆矩阵可视化与算法查准率，查全率对比：
pos acc:0.724880, neg acc:0.860400, total acc:0.792640
可以发现，准确率其实一般。
去除 Stop Words:
事实上，在现实应用场景下的自然语言处理任务时，我们往往不仅考虑一个词语出现的频率，还会考虑到这个词语的类别区分能力。举个例子，对于英语而言，一些形如“a”, “the”, “an”, "it"的介词，连词，人称代词在文本中的出现频率往往是最高的，然而这些词对于文本类别的区分度往往没有任何贡献，换句话说，在任何类别的文本中，这些词的出现频率几乎是一样的，因此仅凭借这些词语往往不能改变文本分类时的似然函数倾向，在NLP中，这些词叫做“停用词(Stop Words)”。以TF-IDF算法分析，Stop Words往往是TF很大而IDF很小。
去除一段文本中的停用词不仅能够提升算法的训练效率，有时还能改善算法的分类准确度。
我们可以再可视化一下原始的词频向量，它其实长这样：
前面的高频词往往都是一些StopWords，它们的出现频率实在是太高了，其他词语的词频在它们面前几乎显得黯然失色。
在imdb数据集中并没有提供stop words词袋，为了方便我们直接选取前50个出现频率最高的词作为stopwords：
# 文本预处理
def cutTopN(X, bow, n):
for i in trange(len(X)):
# 去除重复的词(可以去除看看效果)
# X[i] = np.unique(X[i])
# 去除常用词
for pattern in bow[sort_hist[:n]]:
idx = np.where(X[i]==pattern)[0]
if len(idx) != 0:
X[i] = np.delete(X[i], idx)
return X
[‘the’ ‘and’ ‘a’ ‘of’ ‘to’ ‘is’ ‘it’ ‘in’ ‘i’ ‘this’ ‘that’ ‘was’ ‘as’
‘for’ ‘with’ ‘movie’ ‘but’ ‘film’ ‘on’ ‘not’ ‘you’ ‘he’ ‘are’ ‘his’
‘have’ ‘be’ ‘one’ ‘!’ ‘all’ ‘at’ ‘by’ ‘an’ ‘who’ ‘they’ ‘from’ ‘so’
‘like’ ‘there’ ‘her’ ‘or’ ‘just’ ‘about’ ‘if’ ‘has’ ‘out’ ‘what’ ‘?’
‘some’ ‘good’ ‘more’]
混淆矩阵可视化与算法查准率，查全率对比：
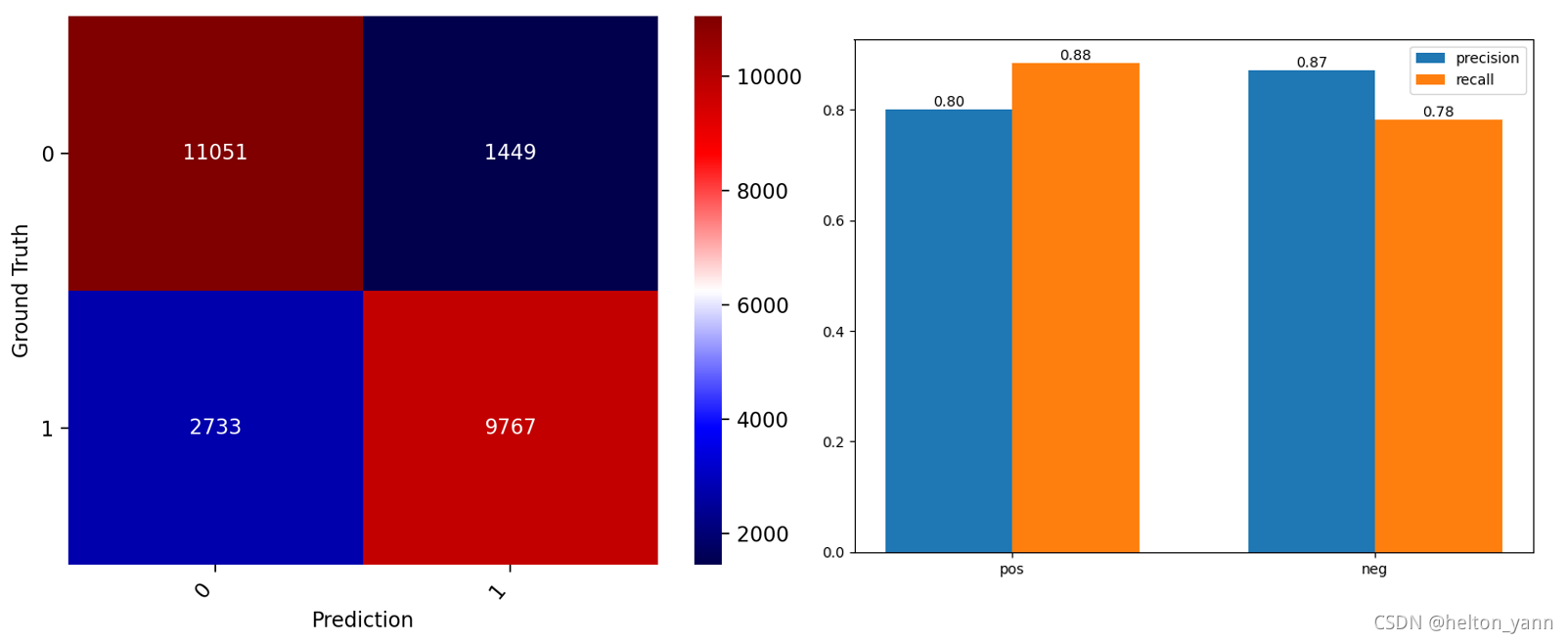
pos acc:0.781360, neg acc:0.884080, total acc:0.832720
精度对比未去除stopwords时有所提升。
对比precision/recall直方图可以发现，正样本的召回率总是较高而负样本的召回率总是较低，一个个人的猜测是人们对于好看的电影总是不加修饰的赞扬而对于批判的言论则倾向于用隐晦的词语表达(总之和数据的特征有关)
5. 算法优缺点总结
缺点：
算法的缺点其实很明显，那就是朴素贝叶斯假定不同特征之间相互独立，然而事实上并不是如此，并且大多数情况下这个假设并不成立。一个很好的例子便是当下Transformer架构的兴起及其在NLP以及CV领域的优异表现。transformer基于的自注意力机制很好说明了数据与数据之间存在着相互关联，并不是假设中的完全相互独立。所以说无法寻找数据之间的关联是朴素贝叶斯算法最大的局限性。
优点：
算法的优点和生成式模型有关。就如文章开头所述，相对于判别式模型学习到的类别与类别之间耦合的特征，生成式模型会对数据的全类别建模，以更为全面的角度考察数据的分布以及类别之下更为深刻的细节。
机器学习实验专栏系列文章：
【机器学习实验一】手撕 kNN(K-Nearest Neighbor, k最邻近算法)
【机器学习实验二】决策树(Decision Tree)及其在图像识别任务上的应用
【机器学习实验三】纯手撕三种朴素贝叶斯算法(Naive Bayes)，并进行IMDB影评数据集分类及手写数字识别
扫一扫
289
到【灌水乐园】发言
