条件概率、乘法概率、全概率、贝叶斯

本人是初学者一枚，写下笔记分享自己的一些见解，若有错误之处希望各位大神多多海涵，并请指出理解有误的地方，谢谢

条件概率公式

Ω样本空间中，A,B两个事件P(B)>0,在B已经发生的条件下A发生的概率，A对B的条件概率P(A|B)。
P(A)是无条件概率->样本空间为Ω
P(A|B)是条件概率->样本空间发生变化，B发生的前提下，以B为样本空间

方法一：
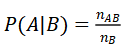其中nB代表B中的样本点数量，nAB代表B发生的前提下A也发生，也就是AB都发生。

方法二：

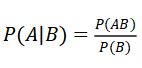
注意条件概率就是样本空间发生了变化。

例子：

编号1-6号的球总共6个，从中随机取一个观察其号码，B事件代表从中取到的球编号为偶数，A1事件取到1号球，A2事件取到2号球，A3事件取到的球编号大于4
问题1：P(A1)=1/6,P(A1|B)=0(取到偶数编号球的前提下，取到1号球的概率)
问题2：P(A2)=1/6,P(A2|B)=1/3(取到偶数编号球的前提下，取到2号球的概率)
问题3：P(A3)=1/3,P(A3|B)=1/3(A3事件会取到5、6号球，而B事件取到2、4、6号球，也就是不会出现5号球)

乘法公式

由之前的条件概率可以推出：


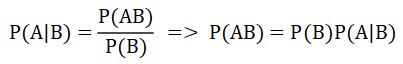
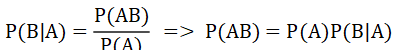
前提条件P(A)>0,P(B)>0，则可以得出乘法公式为：

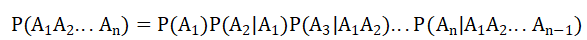
这个公式可以这么理解，笼统的概括把它分为n步，假设A1,A2…An都正确，第一步是正确的也就是P(A1)，然后在第一步是正确的前提下，第二步是正确的也就是P(A2|A1)，然后在第一第二步都正确的前提下，第三步是正确的，P(A3|A1A2)…如此类推，直到后面的在第一第二…第n-1步都正确的前提下，第n步是正确的P(An|A1A2…An-1)。

图示

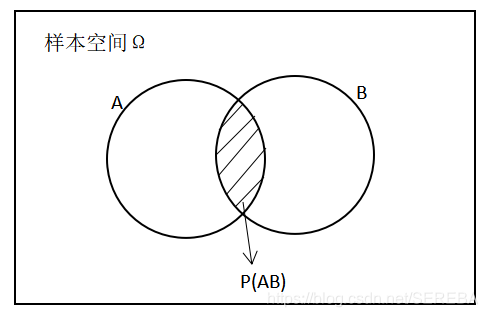
全概率公式

A1,A2…An是实验E的完备事件组，完备事件组条件1、事件之间互不相容，2、全部事件的并集是样本空间Ω,且P(Ai)>0,则全概率公式P(B)：

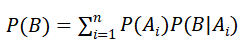
例子

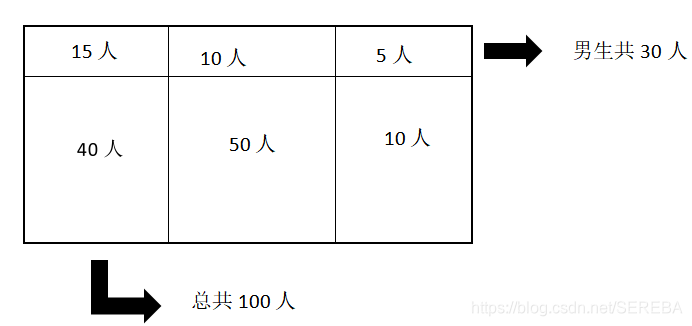
事件B为性别是男生的事件，而A1、A2、A3，把样本点分成三排，分别对应上面第一列，第二列，第三列。则有全概率P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)=40/10015/40+50/10010/50+10/100*5/10,相当于把要求得事件B分成三部分，每一小部分取求解。

贝叶斯公式

全概率公式是知道事件的原因推出结果(因->果)，而贝叶斯公式是知道事件的结果再推出原因(果->因)。
A1,A2…An是实验E的完备事件组，B是其中任意的一个事件，且P(Ai)>0,P(B)>0，求P(Ak|B),已经知道结果B事件发生，求是Ak个原因导致的。

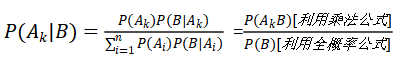
其中P(Ai)是先验概率，已经明确的概率，P(Ai|B)是后验概率，不明确的概率，已知结果求解原因。
仔细观察上面的公式会发现，在乘法公式（利用条件概率推出的）的时候出现过的两条公式：

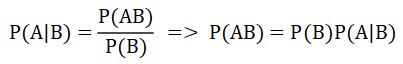
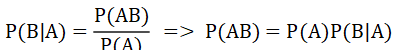
其中结果都是P(AB)，也就是可以通过变形得到：

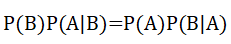
移动一下就会发现，这样得出来的刚好就是贝叶斯公式。