题目描述:
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
(在离散数学里面学习过同构这个概念)百度百科-同构 当然要看懂 最好学习一下代数系统
输入:
N 结点数
结点名称 左孩子下标 右孩子下标(结点名称英文大写字母 左右孩子下标 按0到n-1编号 第几行就对应第几个)
后面再按相同方式给出一棵树的信息
输出:
Yes No (就首字母大写)
#include <stdio.h>
#include <stdlib.h>
#define null -1
typedef struct {
char c;
int left;
int right;
}tree;
tree t1[10];
tree t2[10];
int buildTree(tree t[]){
int n,i,root = null;
char left,right;
scanf("%d\n",&n);
int check[n];
if(n){
for(i = 0; i < n;++i)
check[i] = 0;
for(i = 0; i < n;++i){
scanf("%c %c %c\n",&t[i].c,&left,&right);
if(left != '-'){
t[i].left = left-'0';
check[t[i].left] = 1;
}else
t[i].left = null;
if(right != '-'){
t[i].right = right-'0';
check[t[i].right] = 1;
}else
t[i].right = null;
}
for(i = 0; i < n;++i)
if(!check[i])
break;
root = i;
}
return root;
}
int isomorphic(int r1,int r2){
if((r1 == null) && (r2 == null))
return 1;
if(r1==null&&r2!=null || r1!=null&&r2==null)
return 0;
if(t1[r1].c != t2[r2].c)
return 0;
//左树都不空 且元素相等 不需要旋转
if( (t1[r1].left != null && t2[r2].left != null)
&& (t1[t1[r1].left].c == t2[t2[r2].left].c) )
return isomorphic(t1[r1].right,t2[r2].right)&&
isomorphic(t1[r1].left,t2[r2].left);
else
return (isomorphic(t1[r1].left,t2[r2].right)&&
isomorphic(t1[r1].right,t2[r2].left));
}
int main (){
int r1,r2;
r1 = buildTree(t1);
r2 = buildTree(t2);
if(isomorphic(r1,r2))
printf("Yes");
else
printf("No");
return 0;
}
整体设计
树的存储选择
按照题目来,题目就是想你用静态链表的方式去存放树,按这个方式去定义树的结点就行了。
建树
建树需要注意根节点并不一定是第一个
所以需要去寻找根结点。
根结点就是那个没有一个指向它的结点
所以添加一个数组去标记哪些点是输入结点的孩子
通过一次遍历就可以找出根结点
其次需要注意的就是
读取数据按字符形读取
因为空指针是用字符-表示的
对于不是-的就是数组的下标
去做一下转换就好了(字符是特殊的整形)
判断是否同构
两棵树根都为空
同构
有一棵树根为空而另一个不为空
不同构
两个根都不为空但是结点值不同
不同构
两棵树左子树都不为空且左子树的结点值相同
判断俩个左子树同构 两个右子树是否同构
否则
判断 左右 右左是否同构
这个同构函数所有的判断语句都是同级的啊
不是else if这种 这个还是得稍微注意一下
同构的判断是需要递归进行思考的。
最主要的还是最后一个判断,前面的很简单。
因为同构是可能会交换,所以就可能需要交换两棵树,而需要交换两棵树的情况就是
当前的结点值相同(不相同就可以判段了)
但是两棵树的左子树的结点值不一样,那么就可能需要交换,因为可能是把一颗树把右子树换过来了。
最后这个按照这个逻辑写,在没出问题的情况下,是没问题的。
(我当时最离谱的错误是把左右交换判断那里 写成了左左 左右,愣是看了半天才发现 汗)
题目测试数据
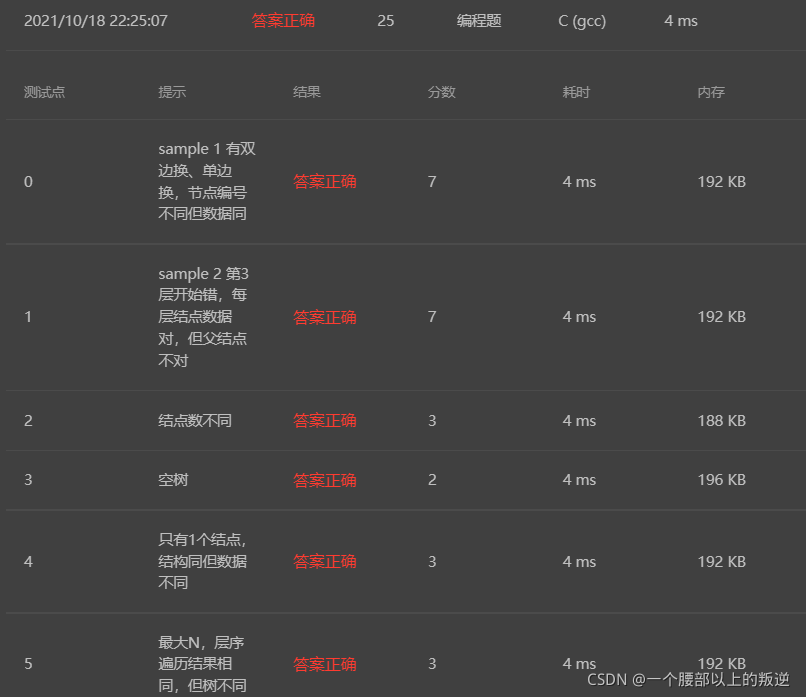




 本文介绍了一种用于判断两棵树是否同构的算法,该算法基于静态链表存储树结构,并通过递归比较节点及其子树进行判断。在C语言中实现,包括建树和同构检查功能。主要思路是检查根节点是否存在,节点值是否相等,以及左右子树的同构性。注意左右子树的同构判断可能需要考虑交换情况。
本文介绍了一种用于判断两棵树是否同构的算法,该算法基于静态链表存储树结构,并通过递归比较节点及其子树进行判断。在C语言中实现,包括建树和同构检查功能。主要思路是检查根节点是否存在,节点值是否相等,以及左右子树的同构性。注意左右子树的同构判断可能需要考虑交换情况。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








