二叉树非递归遍历（先序、中序、后序）

首先是一个二叉树结构：

class TreeNode{
    public int value;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(){
    }
    public TreeNode(int v){
        value=v;
    }

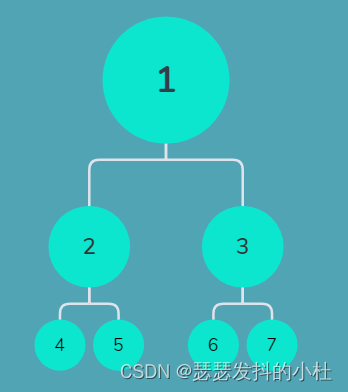
非递归的二叉树遍历需要用到栈的先进后出。

先序遍历

步骤：

1、首先定义一个当前正在检索的结点curNode，将头结点入栈。

2、进入while循环，只有当栈中没有结点时才跳出循环。

3、弹出一个节点赋予curNode，打印这个结点的值。

4、判断当前结点是否有右孩子，有则入栈，判断当前节点是否有左孩子，有则入栈。（注意：此处先入栈右孩子的原因是栈先进后出的特性）

5、重复2~4的步骤直到循环结束。

代码实现：

    //二叉树的非递归遍历 先序
    public static void unorderedTraverse(TreeNode head){
        if(head==null){
            return;
        }
        Stack<TreeNode> stack=new Stack<>();
        stack.push(head);
        TreeNode curNode;
        while (!stack.isEmpty()){
            curNode=stack.pop();
            System.out.print(curNode.value+" ");
            if(curNode.right!=null){
                stack.push(curNode.right);
            }
            if(curNode.left!=null){
                stack.push(curNode.left);
            }
        }
    }

结果：

 

后序遍历

为何先讲后序遍历是因为后序遍历和先序遍历很相似，先序遍历是头左右，后序遍历是左右头，那有人就想了，如果在左右孩子入栈的时候先入左孩子，再入右孩子，是不是就能实现后序遍历了？答案很接近了，如果按是上述实现，得到如下结果：

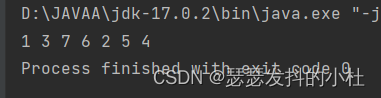
我们想要得到的结果是，4，5，2，6，7，3，1

刚好是反序，那我们只需要用一个数组存储下来再倒序输出就好了。

代码实现：

    //二叉树的非递归遍历 后序
    public static void unorderedTraverse(TreeNode head){
        if(head==null){
            return;
        }
        Stack<TreeNode> stack=new Stack<>();
        stack.push(head);
        TreeNode curNode;
        //存储结果，让结果倒序输出；
        Stack<TreeNode> result=new Stack<>();
        while (!stack.isEmpty()){
            curNode=stack.pop();
            result.push(curNode);
            if(curNode.left!=null){
                stack.push(curNode.left);
            }
            if(curNode.right!=null){
                stack.push(curNode.right);
            }
        }
        //倒序输出
        while (!result.isEmpty()){
            System.out.print(result.pop().value+" ");
        }
    }

结果：

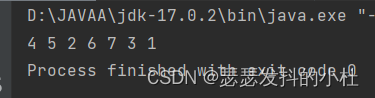
中序遍历：

步骤：

1、判断当前节点是否为null，不为null则入栈，让当前节点更新到当前节点的左孩子直到当前结点为null。

2、更新当前节点为其父节点，输出当前节点的值，让当前节点更新为其右孩子，再一直让当前结点的左孩子判断入栈。

4、重复2~3，直到栈空且当前节点为空。

代码实现：

    //二叉树的非递归遍历 中序
    public static void unorderedTraverse(TreeNode head){
        if(head==null){
            return;
        }
        Stack<TreeNode> stack=new Stack<>();
        TreeNode curNode=head;
        while (!stack.isEmpty()||curNode!=null){
            if(curNode!=null){
                stack.push(curNode);
                curNode=curNode.left;
            }else {
                curNode=stack.pop();
                System.out.print(curNode.value+" ");
                curNode=curNode.right;
            }
        }
    }

 结果：