逻辑回归可以说是互联网领域应用最广的自动分类算法:从单机运行的垃圾邮件自动识别程序到需要成百上千台机器支撑的互联网广告投放系统,其算法主干都是LR。
一句话概括逻辑回归:
逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的。
线性回归
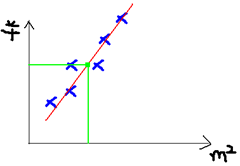
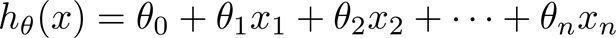
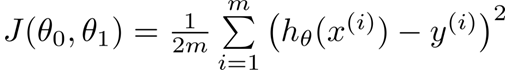
二分类问题
y
∈
0
,
1
y\in{0, 1}
y∈0,1
如果在线性模型上直接做分类。最直观的,可以将线性模型的输出值再套上一个函数,最简单的就是“单位阶跃函数”。
但是这个函数在x=0处不可导,所以我们找到了Logistics函数
y
=
1
1
+
e
−
z
y=\frac{1}{1+e^{-z}}
y=1+e−z1
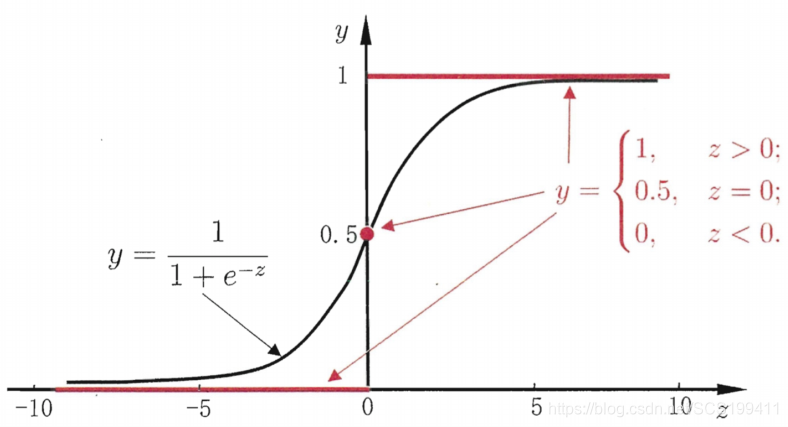
假设函数
h
θ
(
x
)
=
g
(
θ
T
x
)
=
1
1
+
e
−
θ
T
x
h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}
hθ(x)=g(θTx)=1+e−θTx1
l
n
h
θ
(
x
)
1
−
h
θ
(
x
)
=
θ
T
x
ln\frac{h_\theta(x)}{1-h_\theta(x)}=\theta^Tx
ln1−hθ(x)hθ(x)=θTx
记
P
(
y
=
1
∣
x
;
θ
)
=
h
θ
(
x
)
P
(
y
=
0
∣
x
;
θ
)
=
1
−
h
θ
(
x
)
P(y=1|x;\theta)=h_\theta(x) \\ P(y=0|x;\theta)=1-h_\theta(x)
P(y=1∣x;θ)=hθ(x)P(y=0∣x;θ)=1−hθ(x)
损失函数
综合起来表示概率
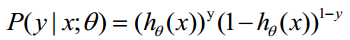
似然函数为
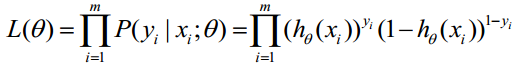
对数似然函数为
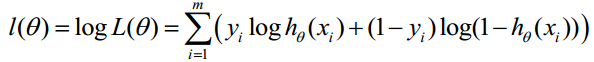
损失函数如下
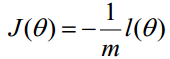
求解方法:梯度下降法、牛顿法、拟牛顿法
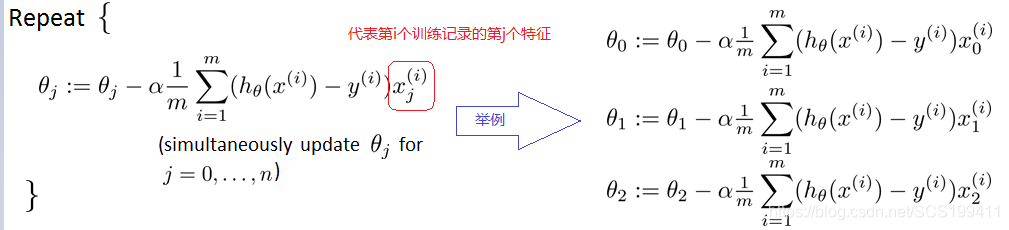
梯度下降法
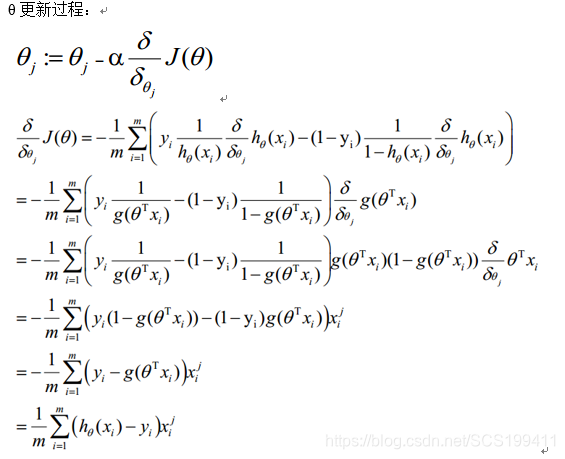
三种梯度下降
- 批量梯度下降 全局最优,计算量大,训练过程慢
- 随机梯度下降 训练速度快,局部最优
- 小批量梯度下降 减少了参数更新的次数,可以达到更加稳定收敛结果
L1和L2正则化
过拟合:对训练数据拟合好,而在测试数据上表现差,泛化能力差。
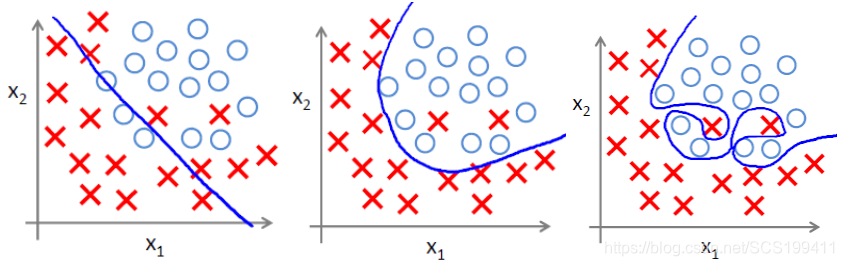
正则化就是在原来的损失函数上加入一个惩罚项。
L1正则化,有助于生成一个稀疏权值矩阵,进而可以用于特征选择。
f
(
θ
)
=
J
(
θ
)
+
λ
∣
∣
θ
∣
∣
1
f(\theta)=J(\theta) + \lambda||\theta||_1
f(θ)=J(θ)+λ∣∣θ∣∣1
L2正则化,拟合过程中通常都倾向于让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。
f
(
θ
)
=
J
(
θ
)
+
λ
2
∣
∣
θ
∣
∣
2
2
f(\theta)=J(\theta)+\frac{\lambda} {2}||\theta||^2_2
f(θ)=J(θ)+2λ∣∣θ∣∣22
优点
- 形式简单,模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响。
- 模型效果不错。在工程上是可以接受的(作为baseline),如果特征工程做的好,效果不会太差。
- 训练速度较快。分类的时候,计算量仅仅只和特征的数目相关。
缺点
- 准确率并不是很高。因为形式非常的简单(非常类似线性模型),很难去拟合数据的真实分布。
- 很难处理类别不平衡的问题。比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。
- 只能处理线性可分二分类的问题。
关于逻辑回归更深入的理解,参考
逻辑回归:从入门到精通





 逻辑回归是互联网领域应用广泛的自动分类算法,假设数据服从伯努利分布,通过极大化似然函数、运用梯度下降求解参数实现二分类。介绍了线性回归、假设函数、求解方法,如梯度下降法等,还提及L1和L2正则化,分析了其优缺点。
逻辑回归是互联网领域应用广泛的自动分类算法,假设数据服从伯努利分布,通过极大化似然函数、运用梯度下降求解参数实现二分类。介绍了线性回归、假设函数、求解方法,如梯度下降法等,还提及L1和L2正则化,分析了其优缺点。
















 527
527

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








