线性规划问题

目录

线性规划模型及其概念

线性规划模型的三要素

建立线性规划模型的三个步骤

灵敏度分析

线性规划模型及其概念

例1.1 某机床厂生产甲、乙两种机床，每台销售后的利润分别为4千元与3千元。生产甲机床需用机器加工，加工时间分别为每台2小时和1小时；生产乙机床需用三种机器加工，加工时间为每台各一小时。若每天可用于加工的机器时数分别为机器10小时、机器8小时和机器7小时，问该厂应生产甲、乙机床各几台，才能使总利润最大？

基本假设

假设该企业的产品不存在积压，即

产量=销量

模型建立

决策变量——xi (i=1,2)分别表示甲、乙机床每天的产量。

目标函数——总利润z=4x1+3x2达到最大值。

约束条件

①生产甲、乙两种机床所花费的加工时间不能超过A,B,C机器每天的最大可用加工时间故

2x1+x2≤10，

x1+x2≤8，

x2≤7.

②甲乙两种j机床的产量还应该满足非负约束，即

xi≥0,i=1,2.

综上所述

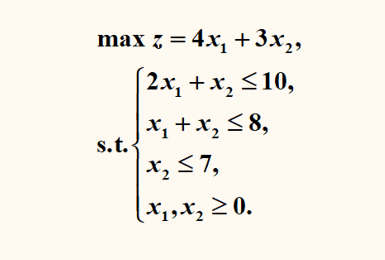
线性规划模型的三要素

（1）决策变量

问题中要确定的未知量，用于表明规划问题中的用数量表示的方案、措施等，可由决策者决定和控制；

（2）目标函数