【LeetCode 37】解数独（递归回溯法）

题目

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 ‘.’ 表示。

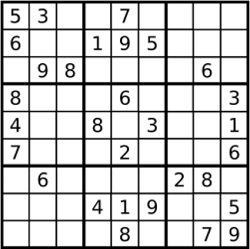
Note:
给定的数独序列只包含数字 1-9 和字符 ‘.’ 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sudoku-solver

题解

此题看似复杂，但其实与经典的“八皇后问题”如出一辙。建议不了解的同学先看“八皇后问题“”。

首先我们先确定数独的三条规则：
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

在此我们用三个二维数组作为数字出现的标记：

struct flag
{
	bool col[9][9] = { false };//col[x][y]=true表示数字y在第x列中出现了
	bool row[9][9] = { false };//row[x][y]=true表示数字y在第x行中出现了
	bool box[9][9] = { false };//box[x][y]=true表示数字y在第x个3x3宫内出现了
	//由于数组从0开始，我们将数字1~9对应到数组0~8号位置
	//例如数字2在第0行出现，则置row[0][2-1]=true
};

数字所在的行和列是明确的，但需要一些转换才能确认数字所在的宫：

int locateBox(int i, int j)//输入数字所在的行列，返回所在宫号
{
	int row = i / 3;
	int col = j / 3;
	return row * 3 + col;
}

现在可以将标记初始化：

void solveSudoku(vector<vector<char>>& board) 
{
	flag tag;
	int size = board.size();

	
	for (int i = 0; i < size; ++i)
	{
		for (int j = 0; j < size; ++j)
		{
			if (board[i][j] != '.')
			{
				int index = board[i][j] - '0' - 1;//board中元素为char型，将其转为int
				tag.row[i][index] = true;
				tag.col[j][index] = true;
				tag.box[locateBox(i, j)][index] = true;
			}
		}
	}

	sudoku(tag, board);//开始递归回溯
	return;
}

初始化完成后开始递归回溯求解：

开始写程序前，我们先手动模拟一下数独的探求方法：

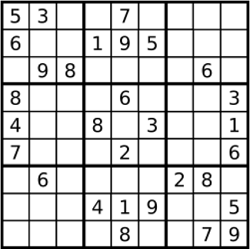
首先，我们可以在[0,2]处填上1

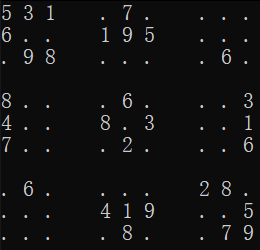
然后以此类推




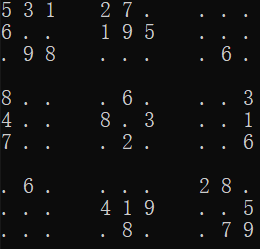
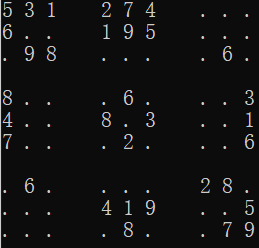
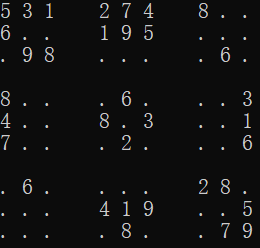
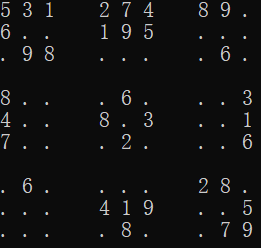
当我们填到[0,8]时，问题出现了，根据规则1~9都无法填入。
这说明之前填入的数字需要修改，于是回退到[0,7]，此时[0,7]的值为9，已无从修改，继续回退，将[0,6]修改为9

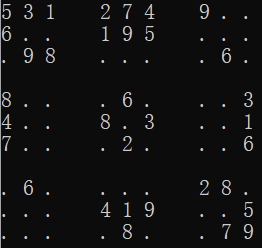
此时[0,7]又无数可填，继续回退，将[0,5]修改为6

以此类推，不断回溯尝试，便可得出一个数独解

以下是递归-回溯代码

bool sudoku(flag& tag, vector<vector<char>>& board)
{
	for (int i = 0; i < 9; ++i)//从左上角开始遍历每一格
	{
		for (int j = 0; j < 9; ++j)
		{
			if (board[i][j] == '.')//遇见没有数字的格，开始尝试填数
			{
				for (int k = 1; k < 10; ++k)
				{
					if (!tag.row[i][k - 1] && !tag.col[j][k - 1] && !tag.box[locateBox(i, j)][k - 1])
					{//如果数k符合三条规则
						board[i][j] = k + '0';//将k填入该格
						if (i==8 && isFinish(board))//当填到最后一行时，每填一个数就扫描整张表，检查是否完成
							return true;
						tag.row[i][k - 1] = true;//填入数后将相应的标记置为true
						tag.col[j][k - 1] = true;
						tag.box[locateBox(i, j)][k - 1] = true;
						if (!sudoku(tag, board))//递归调用
						{
							board[i][j] = '.';//若返回false则说明此路不通，将标志位还原
							tag.row[i][k - 1] = false;;
							tag.col[j][k - 1] = false;
							tag.box[locateBox(i, j)][k - 1] = false;
							if (k == 9)//若1~9都不符合三条规则，则说明先前有数填错，回退
								return false;
						}
						else
							return true;
					}
					else
					{
						if (k == 9)
							return false;//若1~9都不符合三条规则，则说明先前有数填错，回退
					}
				}
			}	
		}
	}
	return true;
}

完整代码：

//board:9*9数独
struct flag
{
	bool col[9][9] = { false };
	bool row[9][9] = { false };
	bool box[9][9] = { false };
};

int locateBox(int i, int j)
{
	int row = i / 3;
	int col = j / 3;
	return row * 3 + col;
}

bool isFinish(vector<vector<char>>& board)
{
	for (int i = 0; i < 9; ++i)
	{
		for (int j = 0; j < 9; ++j)
		{
			if (board[i][j] == '.')
				return false;
		}
	}
	return true;
}

bool sudoku(flag& tag, vector<vector<char>>& board)
{
	for (int i = 0; i < 9; ++i)
	{
		for (int j = 0; j < 9; ++j)
		{
			if (board[i][j] == '.')
			{
				for (int k = 1; k < 10; ++k)
				{
					if (!tag.row[i][k - 1] && !tag.col[j][k - 1] && !tag.box[locateBox(i, j)][k - 1])
					{
						board[i][j] = k + '0';             
						if (i==8 && isFinish(board))
							return true;
						tag.row[i][k - 1] = true;
						tag.col[j][k - 1] = true;
						tag.box[locateBox(i, j)][k - 1] = true;
						if (!sudoku(tag, board))
						{
							board[i][j] = '.';
							tag.row[i][k - 1] = false;;
							tag.col[j][k - 1] = false;
							tag.box[locateBox(i, j)][k - 1] = false;
							if (k == 9)
								return false;
						}
						else
							return true;
					}
					else
					{
						if (k == 9)
							return false;
					}
				}
			}	
		}
	}
	return true;
}

void solveSudoku(vector<vector<char>>& board) 
{
	flag tag;
	int size = board.size();

	
	for (int i = 0; i < size; ++i)
	{
		for (int j = 0; j < size; ++j)
		{
			if (board[i][j] != '.')
			{
				int index = board[i][j] - '0' - 1;
				tag.row[i][index] = true;
				tag.col[j][index] = true;
				tag.box[locateBox(i, j)][index] = true;
			}
		}
	}

	sudoku(tag, board);
	return;
}

int main()
{
	vector<vector<char>> board
	{
		{'5','3','.','.','7','.','.','.','.'},
		{'6','.','.','1','9','5','.','.','.'},
		{'.','9','8','.','.','.','.','6','.'},
		{'8','.','.','.','6','.','.','.','3'},
		{'4','.','.','8','.','3','.','.','1'},
		{'7','.','.','.','2','.','.','.','6'},
		{'.','6','.','.','.','.','2','8','.'},
		{'.','.','.','4','1','9','.','.','5'},
		{'.','.','.','.','8','.','.','7','9'}
	};

	solveSudoku(board);
}