一、进退法及MATLAB实现
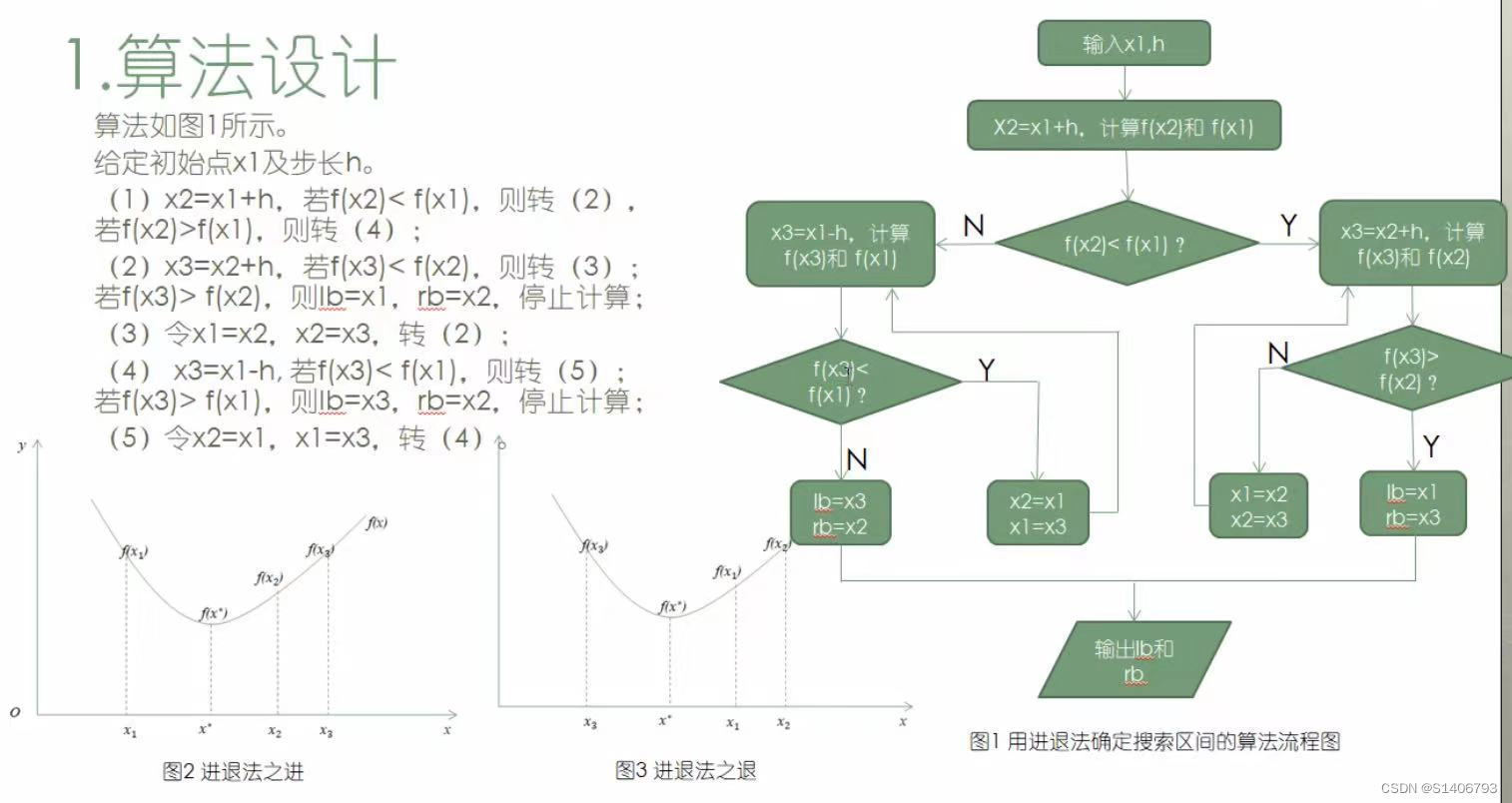
# MATLAB代码
# function [a1,a2,a3]=jintuifa(a1,h)
syms a a1 a2 a3
f=a^2-6*5*a+76;
h=0.1;
% 初始值
a1=2;
a2=a1+h;
f1=subs(f,a,a1);
f2=subs(f,a,a2);
if f1>f2: %这里为进
a3=a2+h;
f3=subs(f,a,a3);
while f3<f2:
a1=a2; %替换
a2=a3;
a3=a2+h; %迭代
f1=subs(f,a,a1);
f2=subs(f,a,a2);
f3=subs(f,a,a3);
end
lb=a1;
rb=a3;
elseif f1<f2: %这里为退
a3=a1-h;
f3=subs(f,a,a3);
while f3<f1:
a2=a1; %替换
a1=a3;
a3=a1-h; %迭代
f1=subs(f,a,a1);
f2=subs(f,a,a2);
f3=subs(f,a,a3);
end
lb=a3;
rb=a2;
end
# 运行
[a,b,c]=jintuifa(0,0.1);
有待深入的问题
- 效率问题:
- 在确定f(x)为单峰函数的情况下,如何确定初始点、步长或二者的组合,使得算法的效率最高?

二、黄金分割法及其MATLAB代码实现
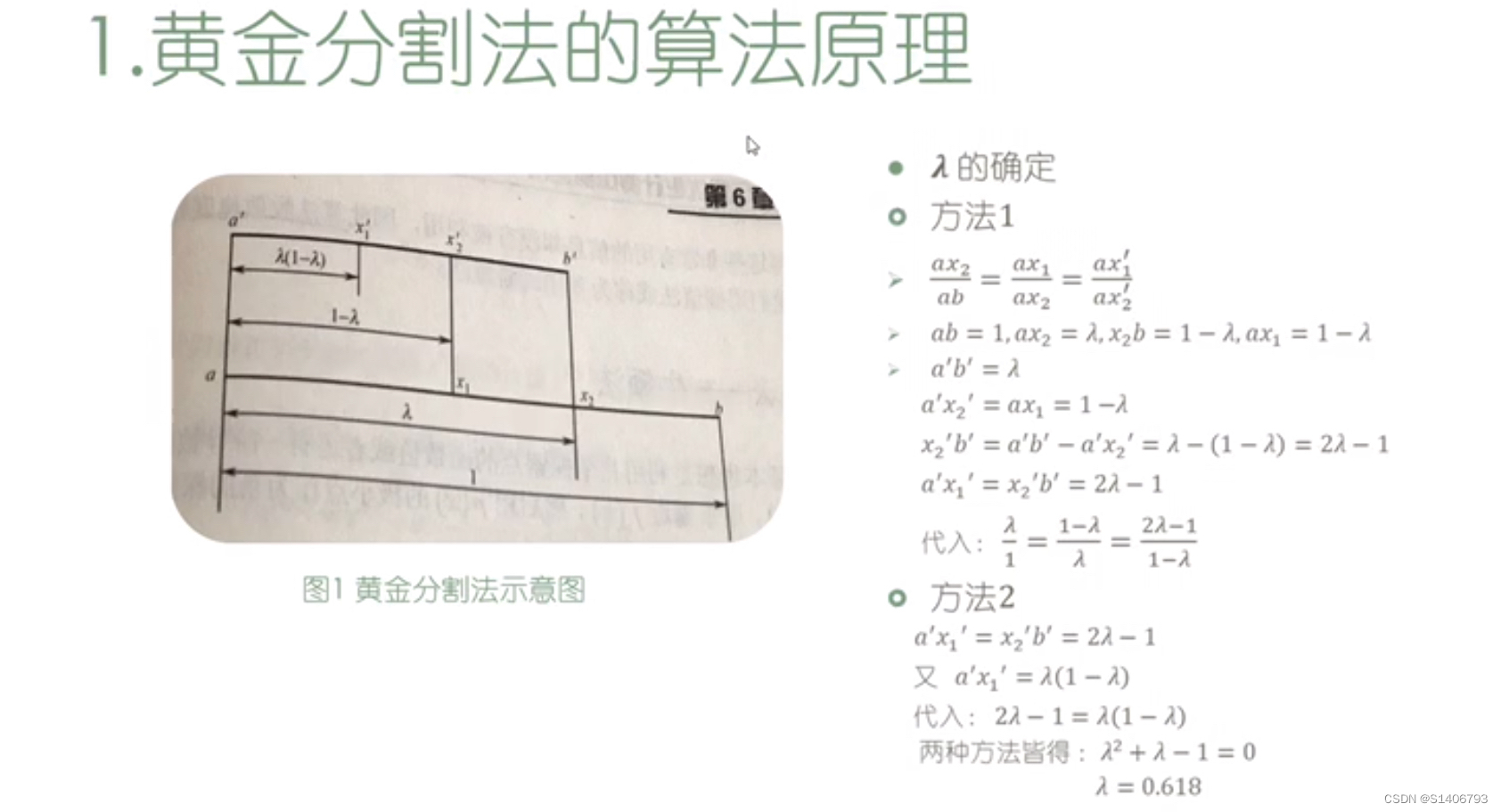
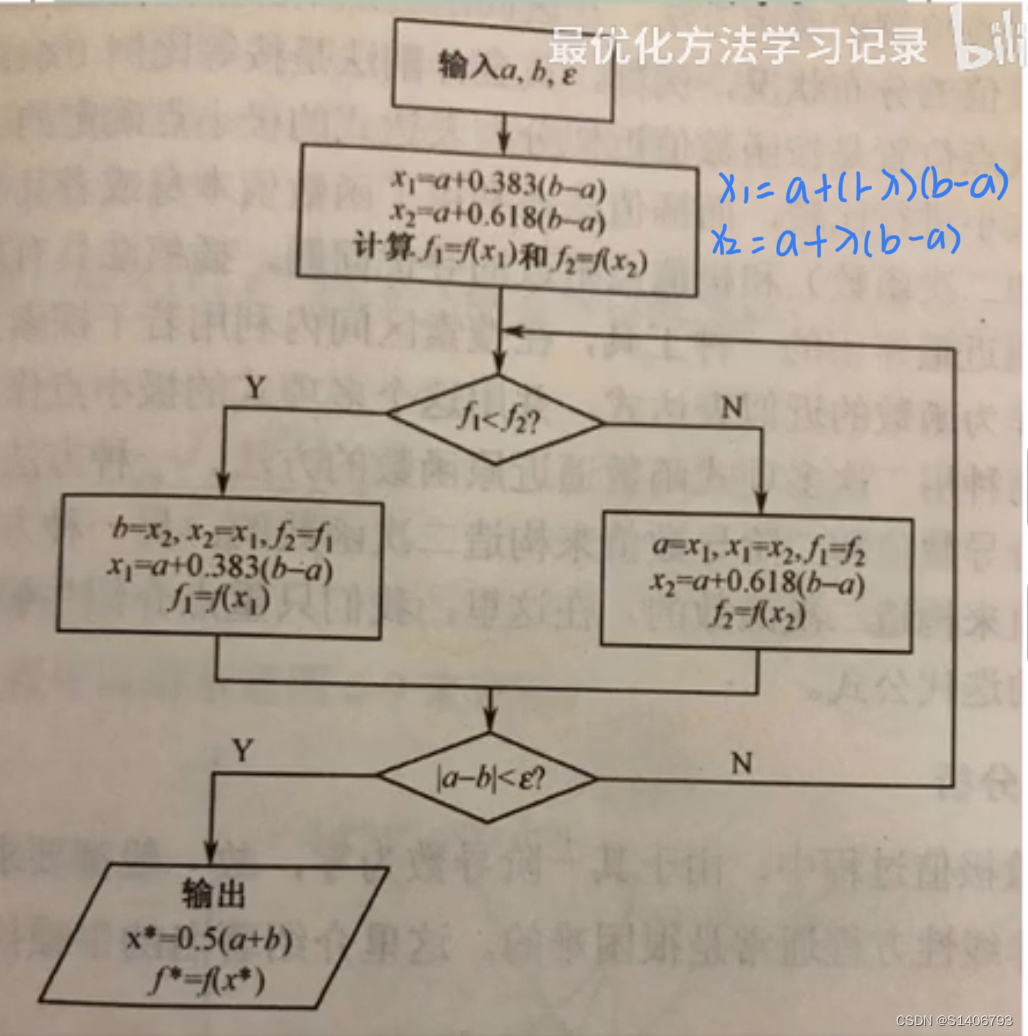
# 黄金分割法
# function x=huangjinfenge(lb,rb,eps)
eps=1.0e-6;
x1=lb+0.383*(rb-lb);
x2=lb+0.618*(rb-lb);
f1=subs(f,a,x1);
f2=subs(f,a,x2);
while abs(rb-lb) > eps % 循环
if f1<f2
rb=x2;
x1=x2;
f2=f1;
x1=lb+0.383*(rb-lb);
f1=subs(f,a,x1);
else % f1 >= f2
lb=x1;
x1=x2;
f1=f2;
x2=lb+0.618*(rb-lb);
f2=subs(f,a,x2);
end
end
xx=(rb+lb)/2;
[a,b,c]=jintuifa(0,0.1);
x=huangjinfenge(a,c,10^-4);
fprintf('黄金分割法:\tx*=%f\tf(x)=%f\n',x,f(x));
- 黄金分割法的缺点
- 该算法对各探索点的函数值都进行了计算,但仅用来比较大小,具体函数值并没有被利用,因此该算法的收敛速度较慢。
- 推荐插值法和多项式逼近法
三、插值法---一维牛顿法及MATLAB代码实现
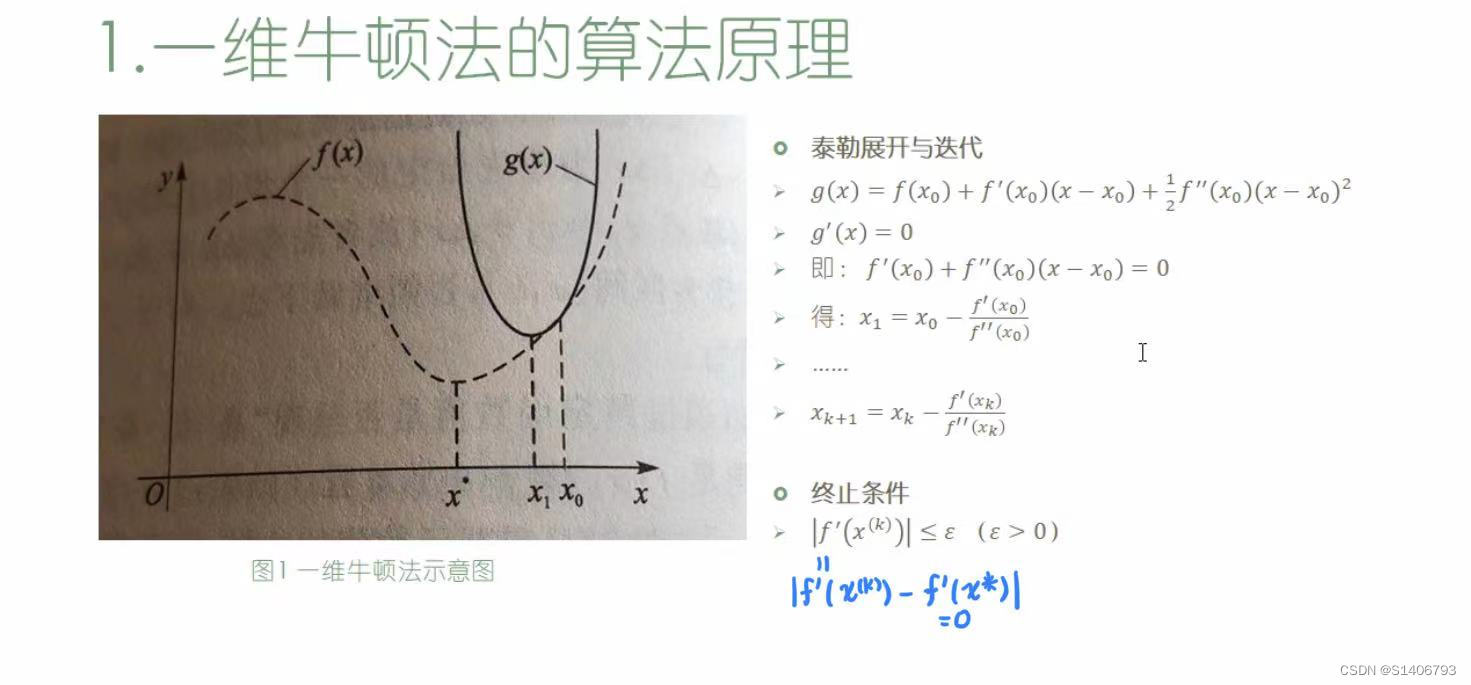
# 一维牛顿法
clear all
clc
% 定义变量、函数f及函数的泰勒展开g
syms x x0 x1
eps=1.0e-6; %定义误差
f=x^4-x^2-1; %定义函数f
x0=4; %定义泰勒展开的初始点
g=taylor(f,3,x,x0) %f在初始点x0的二阶泰勒展开
gp=diff(g,x) %求g的一阶导数gp
x1=solve(gp,x) %令g的一阶导数gp为0,得到g的极小值点
fp=diff(f,x) %求f的一阶导数
fpb=subs(fp,x,x1) %求f在x1处的一阶导数值
c=double(fpb) %把fpb转化为数值,以便于和eps比较
%判断是否满足终止条件,循环
while c>eps
x0=x1 %重新赋值
g=taylor(f,3,x,x0)
gp=diff(g,x)
x1=solve(gp,x)
fpb=subs(fp,x,x1)
c=double(fpb)
end
xx=double(x1) #最优解
minf=subs(f,x1,x)
minf=double(minf)
一维牛顿法的特点
- 优点:收敛速度快。
- 需要注意:只能保证收敛的极限是f(x)的驻点,因此,为了保证收敛到极小点,应要求f''(x)>0,至少对足够大的n如此。
四、插值法---抛物线法及MATLAB代码实现
四、二分法及MATLAB代码实现
lb=0;
rb=1; %根据进退法找到搜索区间
eps=1.0e-6;
middle=(lb+rb)/2; %求中点值
f=2*x^2+4^x-2; %目标函数
fp=diff(f,x); %函数的一阶导数
fpb=subs(fp,x,middle); %一阶导数在中点处的值
while fpb != 0 and abs(rb-lb)>eps %一阶导数值不等于0时,非极小值点
if fbp<0
lb=middle;
end
if fbq>0:
rb=middle;
middle=(lb+rb)/2;
fpb=subs(fp,x,middle);
# 当一阶导数等于0或者搜索区间小于误差时,跳出循环
xx=(rb+lb)/2;

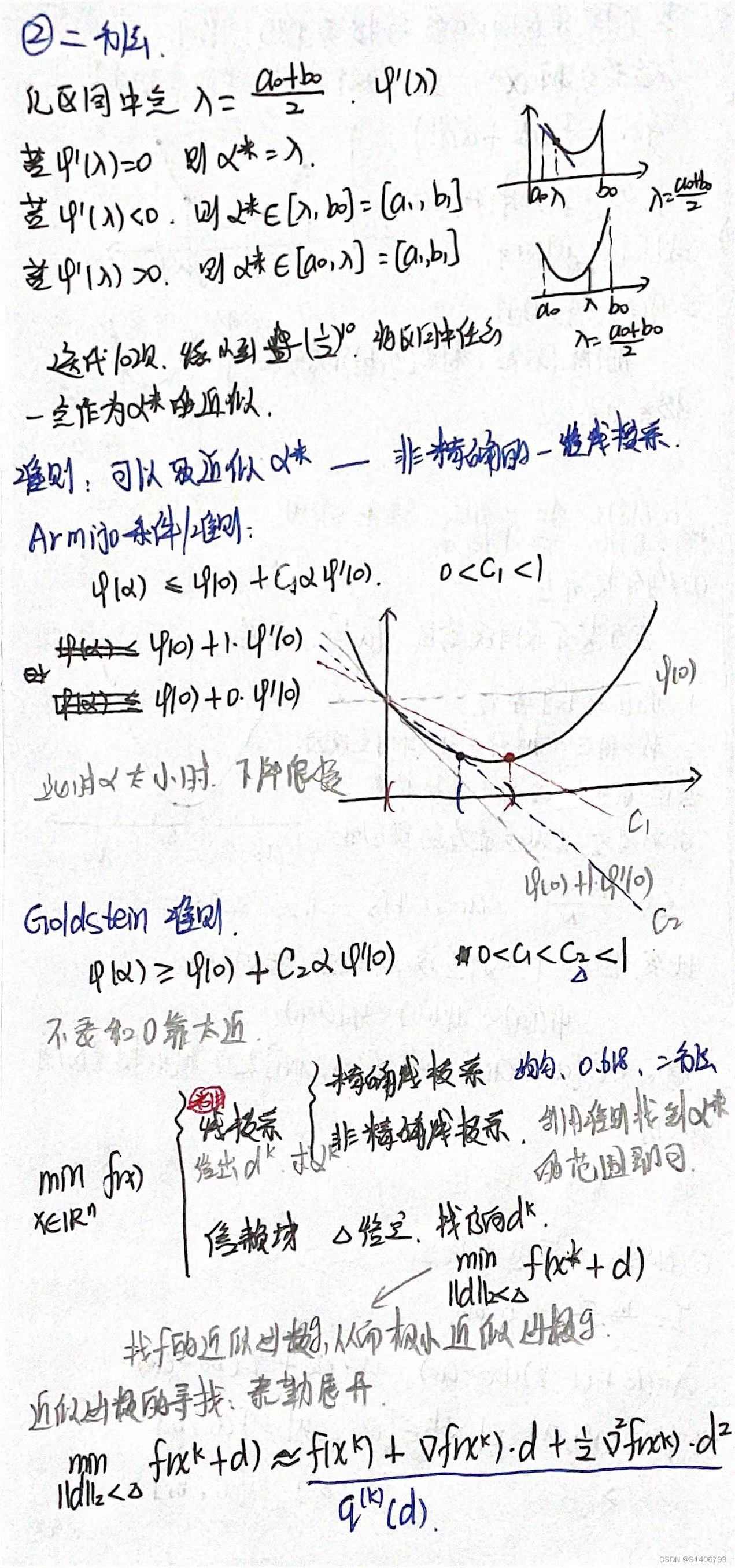





 本文介绍了四种常见的优化算法:进退法、黄金分割法、一维牛顿法和抛物线法,并提供了每种方法的MATLAB实现代码。讨论了算法的优缺点,如黄金分割法虽然简单稳定,但收敛速度较慢;一维牛顿法收敛速度快,但需确保二次导数大于0等。
本文介绍了四种常见的优化算法:进退法、黄金分割法、一维牛顿法和抛物线法,并提供了每种方法的MATLAB实现代码。讨论了算法的优缺点,如黄金分割法虽然简单稳定,但收敛速度较慢;一维牛顿法收敛速度快,但需确保二次导数大于0等。
















 1650
1650

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








