基于comsol的电弧脉冲熔池流动数值模拟，包含马兰戈尼对流

基于comsol的电弧脉冲熔池流动数值模拟，包含马兰戈尼对流（考虑S  P等活性元素，改变马兰戈尼对流流动方向）、表面张力、重力和浮力、以及考虑了热膨胀，耦合了传热、流场以及结构力学

基于COMSOL的电弧脉冲熔池流动数值模拟

引言：
电弧脉冲熔池是一种常用于材料加工的热源，其在金属熔池形成和熔池流动方面具有重要作用。针对电弧脉冲熔池的流动过程，本文基于COMSOL软件进行数值模拟，考虑了马兰戈尼对流、表面张力、重力和浮力以及热膨胀等因素，并耦合了传热、流场和结构力学方程。本文旨在通过详细分析研究电弧脉冲熔池流动的数值模拟方法，探讨活性元素对马兰戈尼对流流动方向的影响，并对实际加工过程中的一些问题进行探讨，欢迎广大同行交流。

1. 引言
电弧脉冲熔池是一种重要的热源，广泛应用于材料加工、焊接和熔覆等领域。在电弧脉冲熔池加工过程中，熔池的形成和流动对于处理材料的性能和工艺控制至关重要。因此，对电弧脉冲熔池的流动进行数值模拟和分析可以提供有价值的工艺参数和性能指标。

2. 模型建立
本文采用COMSOL软件平台的多物理场耦合分析功能，建立了基于电弧脉冲熔池的数值模拟模型。该模型考虑了以下几个主要因素：马兰戈尼对流、表面张力、重力和浮力、热膨胀等。

2.1 马兰戈尼对流
马兰戈尼对流是由活性元素引起的流动，会对电弧脉冲熔池的形态和流动方向产生显著影响。本文通过考虑活性元素的含量和对流效应，模拟了马兰戈尼对流在电弧脉冲熔池中的流动方向，进一步研究了其对材料性能的影响。

2.2 表面张力
表面张力是指液体的表面上存在的分子间的相互作用力。当电弧脉冲熔池形成时，液体表面的张力会影响熔池的形态和流动。本文在模型中考虑了表面张力对电弧脉冲熔池流动的影响，并通过数值模拟分析了其作用机制。

2.3 重力和浮力
重力和浮力是电弧脉冲熔池流动中的重要因素。重力对熔池的形态和流动有影响，而浮力是由于材料熔化引起密度变化而产生的力。本文在模拟中考虑了这两个因素，并通过数值模拟揭示了其对流动行为的影响。

2.4 热膨胀
热膨胀是指材料在受热时由于热量引起其体积的变化。在电弧脉冲熔池流动模拟中，热膨胀会影响熔池的形状和流动。本文考虑了热膨胀对电弧脉冲熔池流动的影响，并通过模拟结果展示了其影响机制。

3. 结果分析
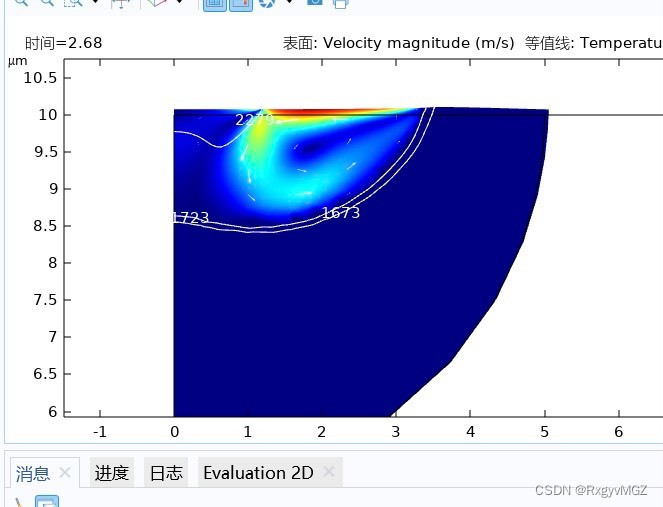
通过对电弧脉冲熔池流动的数值模拟，本文得到了一系列与实验相符合的结果。通过对模拟结果的分析，我们发现了以下几个重要的规律：

3.1 活性元素对马兰戈尼对流流动方向的影响
在电弧脉冲熔池中，活性元素的含量对马兰戈尼对流流动方向有显著影响。随着活性元素含量的增加，马兰戈尼对流的流动方向发生变化。本文通过模拟结果展示了这一规律，并进一步分析了活性元素含量与马兰戈尼对流流动方向之间的关系。

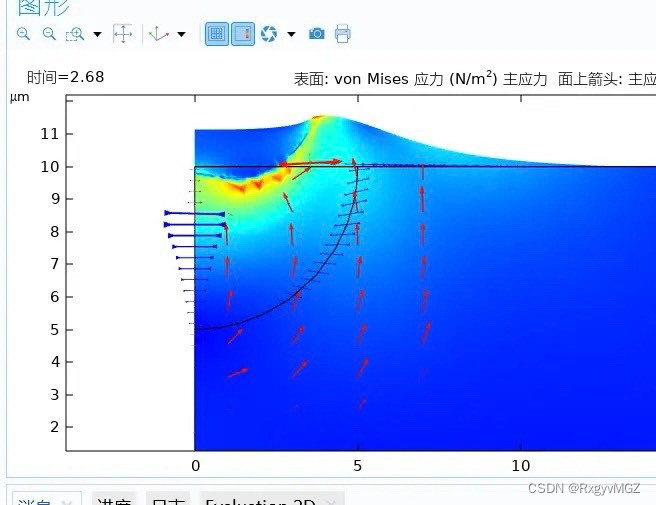
3.2 表面张力对熔池形态的影响
表面张力是电

相关代码,程序地址：http://lanzoup.cn/761857673195.html