笨人小白的温故知新——递归（6）

1205：汉诺塔问题

---

这是一道很经典的题。当然，我一开始也没有做出来，但是！我当时发现了一些规律！只是当时不知道怎么表达而已（傲娇）。

下图，是汉诺塔问题的抽象模型。

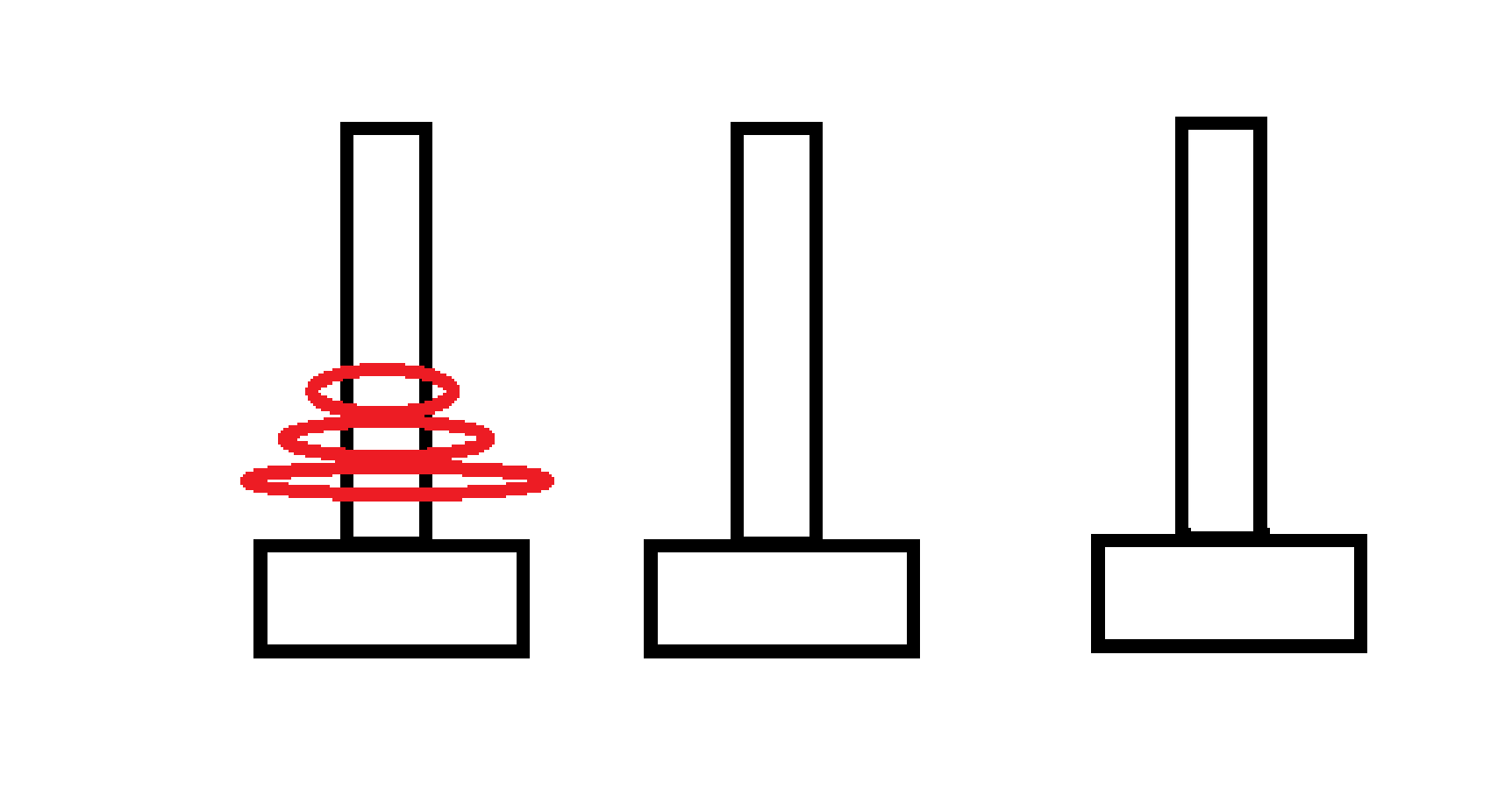
我的发现：

1）因为，小环必须在大环的上面，所以，肯定要借助一根柱子当作“缓停点”。即：我from这里to那里，必须要借助一个aux柱缓一缓。

2）b柱和c柱会在每进行一次“将a柱上的小环拿下放在已排列好的柱上”这一过程中，充当那个“一排列好的柱”，所以，要想让b柱当最后的“已排列好的柱”，在前一个环排列好时，c柱充当的是“已排列好的柱”。

唉~这不就好办了吗。

这道题很明显是个递归问题。那么，我们就按照递归的三大条件，来定义这个hanoi叭~

1）要移出a柱上的第n个环，我们要在移出第n-1的基础上，移第n个环；

2）当然，当移第0个环的时候，就是初始状态，函数就应当停止；

下面是AC代码：

#include <iostream>

using namespace std ;

void hanoi(int n , char from , char to , char aux){
	if (n == 0) return ;
	hanoi(n-1 , from , aux , to) ;
	printf("%c->%d->%c\n", from , n , to) ;
	hanoi(n-1 , aux , to , from) ;
}
int main(){
	int n ;
	char a , b , c ;
	cin >> n >> a >> b >> c ;
	hanoi(n , a , b , c) ;
	return 0 ;
}