【王道】7 动态规划 递推求解

7.1楼梯问题

契波那切数列：1,1,2,3....  第一个是1，第二个也是1，其后，每个数是前两个数之和。

数列为答案排成，f(n)是数列第N个数，也是台阶个数为N是上台阶方式总数

递推关系：考虑最后一步，分为一个台阶，两个台阶到达最后一步,f(i-1)是原来到达i-1方式数量，同理f(i-1).总的步数，求和f(i）=f(i-1)+f(i-2)

注意：循环i=3开始，11d\n控制输出

#include<stdio.h>
long long F[91];//定义数列 1-99
int main (){
	F[1]=1;//初始递推
	F[2]=2;
	for(int i=3;i<=90;i++)
		F[i]=F[i-1]+F[i-2];//所求最后一步的求和
	int n;
	while(scanf("%d",&n)!=EOF){
		printf("%11d\n",F[n]);//判断输入，格式化输出“11”
	}
	return 0;
}

7.2 错排公式

错装方式数量排成数列，f(n)是数列第N个数，也是N个信封的错装总数。

任意一种试错方案做假设，如图

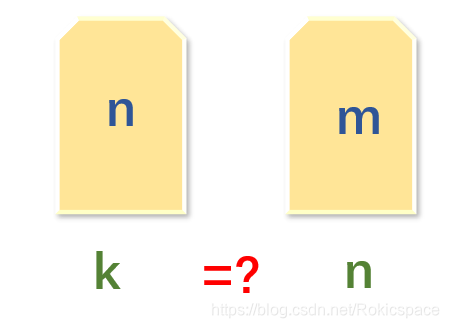
错装公式：f(n)=(n-1)*f(n-1)+(n-1)*f(n-2)

#include<stdio.h>
long long F[91];//定义数列 1-99
int main (){
	F[1]=1;//初始递推
	F[2]=2;
	for(int i=3;i<=90;i++)
		F[i]=(i-1)*F[i-1]+(i-2)*F[i-2];//错排公式
	int n;
	while(scanf("%d",&n)!=EOF){
		printf("%11d\n",F[n]);//判断输入，格式化输出“11”
	}
	return 0;
}