负环——SPFA判断负环

最新推荐文章于 2022-03-24 11:13:03 发布

原创最新推荐文章于 2022-03-24 11:13:03 发布 · 405 阅读

3 ·

CC 4.0 BY-SA版权

图论专栏收录该内容

4 篇文章

订阅专栏

本文详细介绍了如何使用SPFA算法来检测图中是否存在负环。通过实例解释了负环的概念，即边权之和为负的环，并提供了C++代码实现。在SPFA算法中，若一个点的最短路径经过的点数超过n，则说明存在负环。

负环

~~讲的比较难懂，请见谅~~

定义：一个边权之和为负的环。

例如

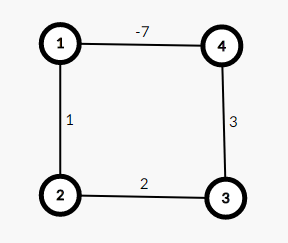
权值和为-1小于0，所以这是负环。

做法：

用SPFA算法，如果走到一个点的最短路中经过的点数超过n，那么说明存在负环。

#include<cstdio>
#include<queue>
#include<vector>
#define maxn 20005
#define maxm 60005
#define inf 0x7fffffff
#define ri register int
int to[maxm];
int weight[maxm];
int next[maxm];
int head[maxn];
int vis[maxn];
int dis[maxn];//1到每个点的最短路 
int sum[maxn];//1到每个点的最短路经过的点的个数 
int T,n,m,cnt,flag;
inline int read()
{
	ri x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
inline void add_edge(int u,int v,int w)
{
	cnt++;
	to[cnt]=v;
	weight[cnt]=w;
	next[cnt]=head[u];
	head[u]=cnt;
}
void SPFA()
{
	std::queue<int>q;
	flag=0;
	sum[1]=1;
	dis[1]=0;
	q.push(1);
	while(q.size())
	{
		ri k=q.front();
		q.pop();
		vis[k]=0;
		for(ri i=head[k];i;i=next[i])
		{
			ri v=to[i],w=weight[i];
			ri s=dis[k]+w;
			if(s<dis[v])
			{
				dis[v]=s;
				sum[v]=sum[k]+1;//关键！当前点的最短路过点数为上个点的+1 
				if(sum[v]>n)//判断最短路经过点数是否超过n 
				{
					flag=1;
					return;	
				}
				if(!vis[v])
				{
					q.push(v);
					vis[v]=1;
				}
			}
		}
	}
}
int main()
{
	T=read();
	for(ri I=1;I<=T;++I)
	{
		n=read(),m=read();
		for(ri i=0;i<=n;++i)//每次清零 
		{
			to[i]=0;
			weight[i]=0;
			next[i]=0;
			head[i]=0;
			sum[i]=0;
			vis[i]=0;
			dis[i]=inf;
		}
		for(ri i=1,u,v,w;i<=m;++i)
		{
			u=read(),v=read(),w=read();
			add_edge(u,v,w);
			if(w>=0) add_edge(v,u,w);
		}
		SPFA();
		if(flag==1) printf("YE5\n");
		else printf("N0\n");
	}
	return 0;
}