基于 Lp 正则化的高维稀疏解的反演

一、稀疏解的逼近问题

对于高维稀疏解的逼近问题，可以归结为模型
$$y=Ax+ϵ$$
其中，$A\in {\mathbb{R}}^{M\times N}$是给定或者训练得到的$M\times N$矩阵，$\mathbf{y}\in {\mathbb{R}}^{\mathbf{M}}$是测得的数据，$ϵ$是扰动噪声。我们的目的是根据已知数据$\mathbf{y},\mathbf{A},ϵ$，来反演高维稀疏解$\mathbf{x}\in {\mathbb{R}}^{\mathbf{N}}$。

机器学习的回归问题中，为了防止过拟合和提高模型泛化性能，对原始损失函数引入额外惩罚项信息，即$L_p$正则化
$$\mathbf{x}=\arg \underset{\mathbf{x}}{\min }{\Vert A\mathbf{x}-\mathbf{y}\Vert }^2+\lambda {\Vert \mathbf{x}\Vert }_{L_p}^p,0\le p\le 2$$
特别的，当$p=0$时，
$${\Vert \mathbf{x}\Vert }_{L_0}=\sum _{i=1}^N{I}_{x_i\ne 0},I_{x_i\ne 0}=\{\begin{array}{cc}1& x_i\ne 0\\ 0& x_i=0\end{array}$$根据不同的问题，选择合适的参数$p$。

$L_1$正则化可以使得参数稀疏化，从而过滤掉模型的一些无用特征，提高模型的泛化能力，降低过拟合的可能。$L_2$正则化可以使得参数平滑，防止模型过拟合。因此对比而言，$L_1$正则化更适合处理高维稀疏数据。

下面以二维为例，从优化问题和概率论角度来讨论为什么$L_1$正则化产生稀疏模型。

1.1、优化问题角度

此时模型的求解转化为如下的优化问题
$$\mathbf{x}=\arg \underset{x}{\min }{\Vert \left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]-\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]\Vert }^2+\lambda \sum _{i=1}^2{\left|x_i\right|}^p$$
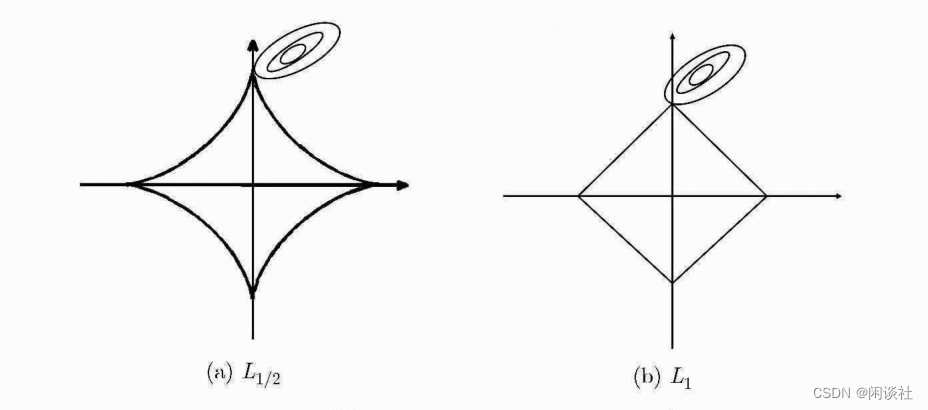
将损失函数$f(x)$投影到$x_1,x_2$平面，即等值线（如图彩色线条），并分别画出$L_1$正则化项和$L_2$正则化项（如图黑色线条）


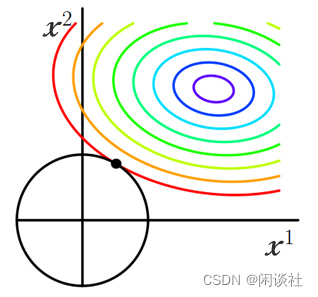
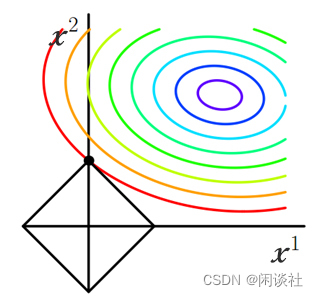
正则化项同拉格朗日乘子的作用一样，起了约束作用。因为当损失函数$f(x)$的等值线与正则化项首次相交的地方就是最优解。从上图可见，$L_1$正则化项比$L_2$多出4个突出的角，当等值线与这些角相交的机率会大大增加。而在这些角上，某个权值$x_i$等于0。当维数增加，$L_1$突出的角更多，因此更容易产生稀疏模型。

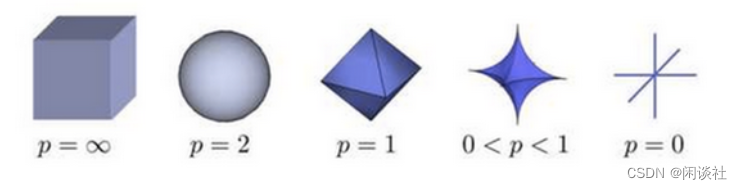
1.2、概率论问题角度}

$L_1$正则化相当于为$\mathbf{x}$加入了Laplace先验分布，而$L_2$正则化项相当于为$\mathbf{x}$加入了Gaussian先验分布。

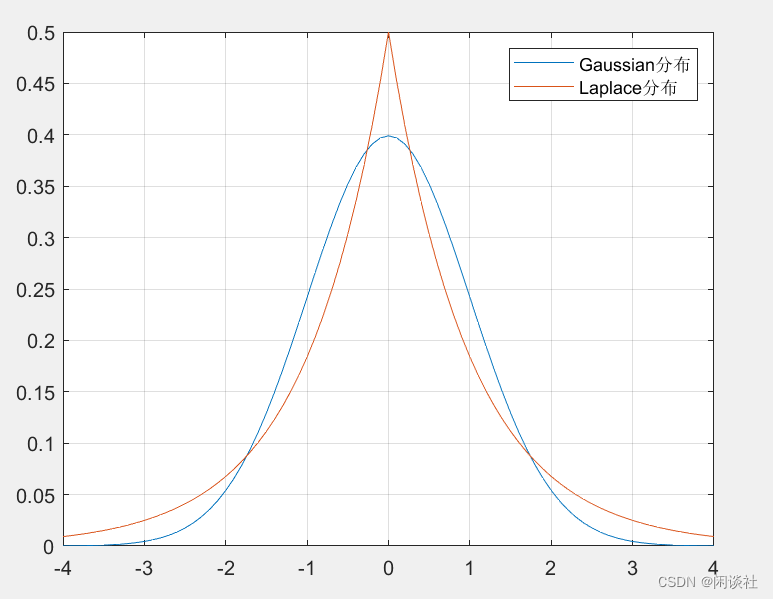
从分布图直观上看，在两端Gaussian分布的概率$p_G(x)$小于Laplace分布的概率$p_L(x)$，且在中间段Gaussian分布等于0和接近0的分布很接近，说明Gaussian分布下的$\bf x $比较均匀。而Laplace分布等于0处的概率远大于其他部分，说明Laplace分布下的x 存在更多的0元素。

二、$L_1$与$L_{1/2}$正则化的求解

2.2、$L_1$的软阈值迭代算法

对于连续可微的无约束优化问题
$$\underset{\mathbf{x}\in \mathbb{R}}{\min }f(\mathbf{x})$$
且满足Lipschitz连续条件
$${\Vert ▽f({\mathbf{x}}_{\mathbf{k}})-▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})\Vert }_2\le L(f){\Vert {\mathbf{x}}_{\mathbf{k}}-{\mathbf{x}}_{\mathbf{k}-1}\Vert }_2$$
根据梯度法，给定初始点$x_0\in R$和初始步长t，有
$${\mathbf{x}}_{\mathbf{k}}={\mathbf{x}}_{\mathbf{k}-1}-\mathbf{t}▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})$$
将$f(\mathbf{x})$在${\mathbf{x}}_{\mathbf{k}-1}$处做二阶泰勒展开，并省略高阶项
$$f(\mathbf{x})=\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})+⟨\mathbf{x}-{\mathbf{x}}_{\mathbf{k}-1},▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})⟩+\frac{⟨{\Vert \mathbf{x}-{\mathbf{x}}_{\mathbf{k}-1}\Vert }_2^2,{▽}^2\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})⟩}{2}$$
结合上述公式，可得
$${\mathbf{x}}_{\mathbf{k}}=\arg \underset{\mathbf{x}}{\min }\left\{\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})+⟨\mathbf{x}-{\mathbf{x}}_{\mathbf{k}-1},▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})⟩+\frac{{\Vert \mathbf{x}-{\mathbf{x}}_{\mathbf{k}-1}\Vert }_2^2}{2\mathbf{t}}\right\}$$
忽略常数项，则上式又可写成
$$\begin{array}{rl}{\mathbf{x}}_{\mathbf{k}}& =\arg \underset{\mathbf{x}}{\min }(▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1}){)}^{\mathbf{T}}(\mathbf{x}-{\mathbf{x}}_{\mathbf{k}-1})+\frac{1}{2\mathbf{t}}(\mathbf{x}-{\mathbf{x}}_{\mathbf{k}-1}{)}^{\mathbf{T}}(\mathbf{x}-{\mathbf{x}}_{\mathbf{k}-1})\\ & =\arg \underset{\mathbf{x}}{\min }\frac{1}{2\mathbf{t}}{\left[\mathbf{x}-({\mathbf{x}}_{\mathbf{k}-1}-2\mathbf{t}▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})\right]}^{\mathbf{T}}(\mathbf{x}-{\mathbf{x}}_{\mathbf{k}-1})\end{array}$$
可见有两个零点，取中点得到函数的最小值
$$\begin{array}{rl}{\mathbf{x}}_{\mathbf{k}}& =\frac{1}{2}\left[{\mathbf{x}}_{\mathbf{k}-1}-2\mathbf{t}▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})+{\mathbf{x}}_{\mathbf{k}-1}\right]\\ & ={\mathbf{x}}_{\mathbf{k}-1}-\mathbf{t}▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})\end{array}$$
将上述的梯度法思想用到$L_1$正则化问题，得到迭代公式
$${\mathbf{x}}_{\mathbf{k}}=\arg \underset{\mathbf{x}}{\min }\left\{\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})+⟨\mathbf{x}-{\mathbf{x}}_{\mathbf{k}-1},▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1})⟩+\frac{{\Vert \mathbf{x}-{\mathbf{x}}_{\mathbf{k}-1}\Vert }_2^2}{2\mathbf{t}}+\lambda {\Vert \mathbf{x}\Vert }_1\right\}$$
忽略常数项，则上式又可写成
$${\mathbf{x}}_{\mathbf{k}}=\arg \underset{\mathbf{x}}{\min }\left\{\frac{{\Vert \mathbf{x}-({\mathbf{x}}_{\mathbf{k}-1}-\mathbf{t}▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1}))\Vert }_2^2}{2\mathbf{t}}+\lambda {\Vert \mathbf{x}\Vert }_1\right\}$$

考虑一般的优化问题
$$\begin{array}{rl}{\mathbf{x}}_{\mathbf{k}}& =\arg \underset{\mathbf{x}}{\min }\left\{\frac{{\Vert \mathbf{x}-\mathbf{s}\Vert }_2^2}{2\mathbf{t}}+\lambda {\Vert \mathbf{x}\Vert }_1\right\}\\ & =\arg \underset{x}{\min }\sum _{i=1}^n\frac{1}{2t}(x_i-s_i{)}^2+\lambda \left|x_i\right|\end{array}$$
令$g(x_i)=\frac{1}{2t}(x_i-s_i{)}^2+\lambda \left|x_i\right|$，对$g(x_i)$求导并令其等于0，
$$\begin{array}{rl}& \frac{\mathrm{d}g}{\mathrm{d}{x}_i}=\frac{1}{t}(x_i-s_i)+sgn(x_i)=0\\ & ⟹x_i=s_i-\lambda t\cdot sgn(x_i)\end{array}$$
即当$x_i>0$时，$x_i=s_i-t\lambda$；当$x_i=0$时，$x_i=s_i=0$；$x_i《0$时，$x_i=s_i+t\lambda$.\
所以，$$\{\begin{array}{ll}{x}_i=s_i-t\lambda & \text{ if }{s}_i>t\lambda \\ x_i=0& \text{ if }-t\lambda \le s_i\le t\lambda \\ x_i=s_i+t\lambda & \text{ if }{s}_i<-t\lambda \end{array}$$
上式可进一步化简，得
$$x_i=\max (\left|s_i\right|-\lambda t,0)\cdot sgn(s_i)=P_{\lambda t}(s)$$
即
$${\mathbf{x}}_{\mathbf{k}}={\mathbf{P}}_{\lambda \mathbf{t}}(\mathbf{s})$$

综上所述，方程的解可写为
$${\mathbf{x}}_{\mathbf{k}}={\mathbf{P}}_{\lambda \mathbf{t}}({\mathbf{x}}_{\mathbf{k}-1}-\mathbf{t}▽\mathbf{f}({\mathbf{x}}_{\mathbf{k}-1}))$$
其中，$P_{\lambda t}$为软阈值算子，步长$t$可取$\frac{1}{L(▽f)}$。

2.1、$L_{1/2}$正则化算法

2008年，徐宗本在《 $L_{1/2}$正则化》中证明,$L_{1/2}$正则化子比$L_1$正则化子具有更好的稀疏性和稳健性。

文献中为了求解$L_{1/2}$正则化问题，提出重赋权迭代求解思想，将$L_{1/2}$正则化问题转化为$L_1$正则化问题
$$x_{k+1}=\arg \underset{x}{\min }{\Vert y-Ax\Vert }_2^2+\lambda \sum _{i=1}^N\frac{\left|x_i\right|}{\sqrt{\left|x_{i,k}\right|}}$$
因为$x_i$可能出现0，为了保证算法可实施，可采用$\frac{1}{\sqrt{|x_{i,k}|}+ϵ}$替代$\frac{1}{\sqrt{|x_{i,k}|}}$，即
$$x_{k+1}=\arg \underset{x}{\min }{\Vert y-Ax\Vert }_2^2+\lambda \sum _{i=1}^N\frac{\left|x_i\right|}{\sqrt{\left|x_{i,k}\right|}+ϵ}$$

三、算例

3.1、例1——高斯分布矩阵

数据源：
1、随机产生$250\times 500$的高斯信号矩阵A，矩阵条件数为 5.5415
2、 随机产生$500\times 1$的高斯分布数据$\mathbf{x}$，再随机令其中20个元素非零，其余为零。。由$A\mathbf{x}=\mathbf{y}$，可3、得到数据$\mathbf{y}$
对得到的数据$\mathbf{y}$，施加$1\%$的随机噪声

计算结果：

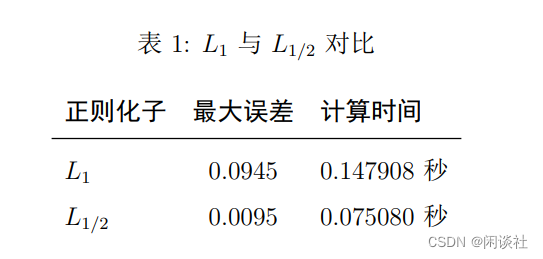
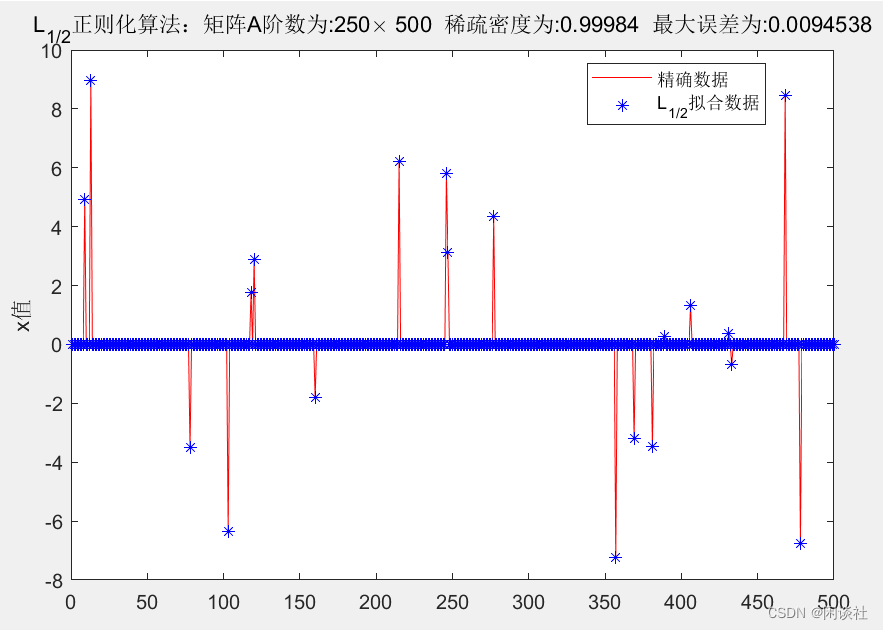
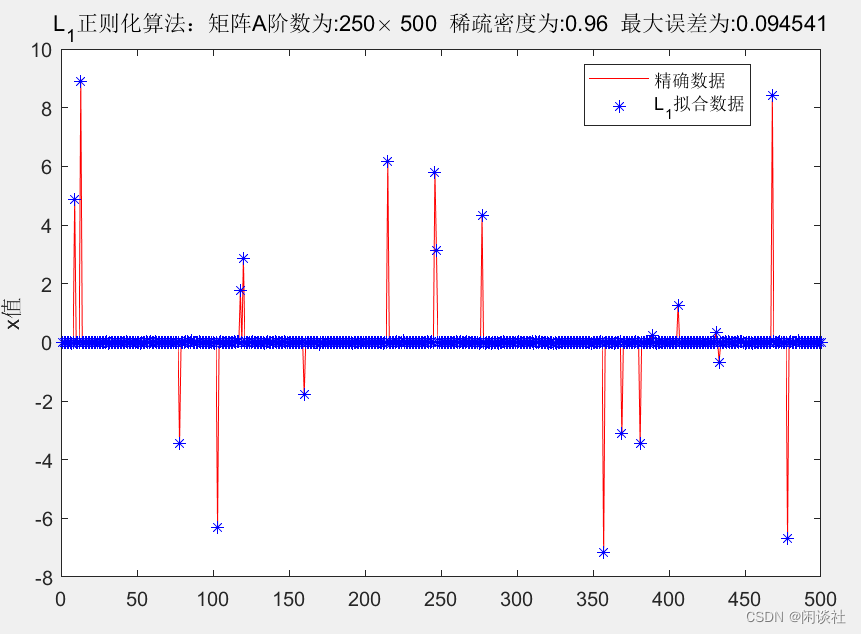
3.2、例2-积分方程

数据源：

1、考虑一个卷积型积分方程例子：
$${\int }_0^{1}K(x,t)g(t)\mathrm{d}t=f(x),0\le x\le 1$$
其中核函数$K(x,t)=e^{xt}$。当核函数矩阵为$20\times 20$时，其条件数为2463.
2、 随机产生$20\times 1$的高斯分布数据$\mathbf{x}$，再随机令其中5个元素非零，其余为零。由$K\mathbf{x}=\mathbf{y}$，可得到数据$\mathbf{y}$
3、对得到的数据$\mathbf{y}$，施加$1\%$的随机噪声

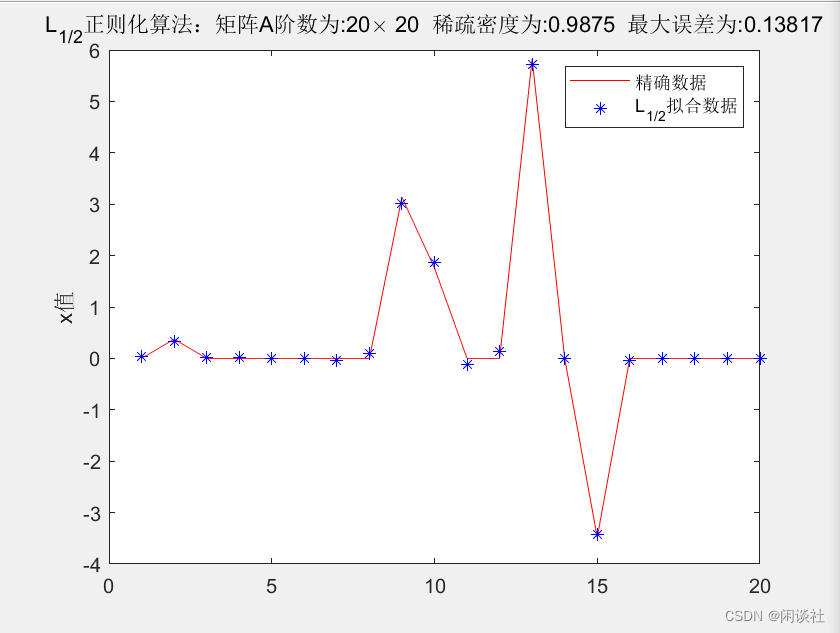
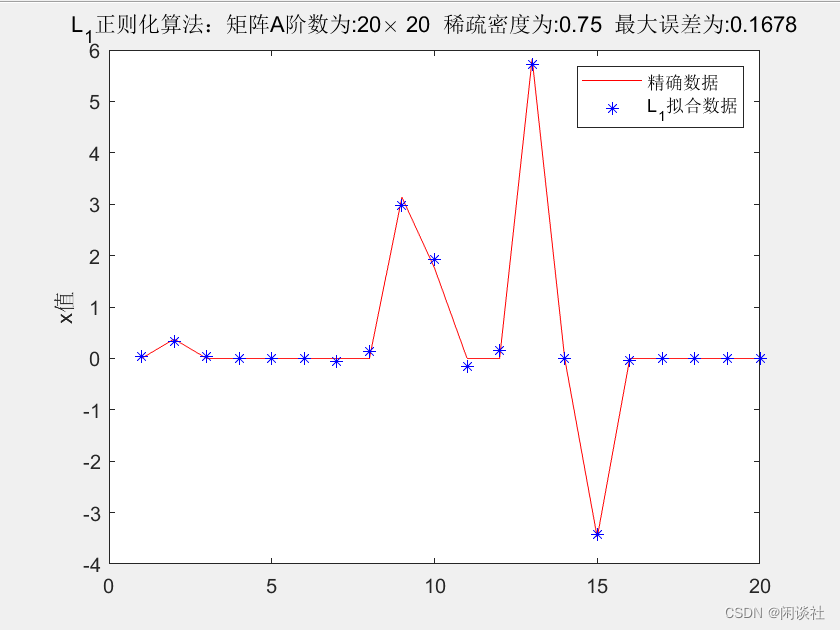
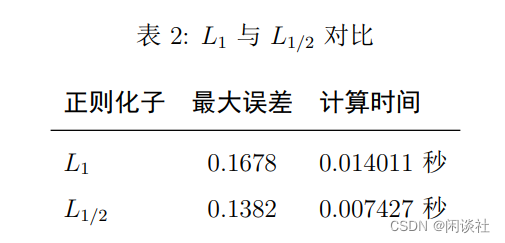
3.3、例3-Hilbert矩阵

数据源：
1、 产生$500\times 500$的Hilbert矩阵A，矩阵条件数为$6.8337\times 10^{20}$
2、随机产生$500\times 1$的高斯分布数据$\mathbf{x}$，再随机令其中20个元素非零，其余为零。由$A\mathbf{x}=\mathbf{y}$，可得到数据$\mathbf{y}$
3、对得到的数据$\mathbf{y}$，施加$1\%$的随机噪声

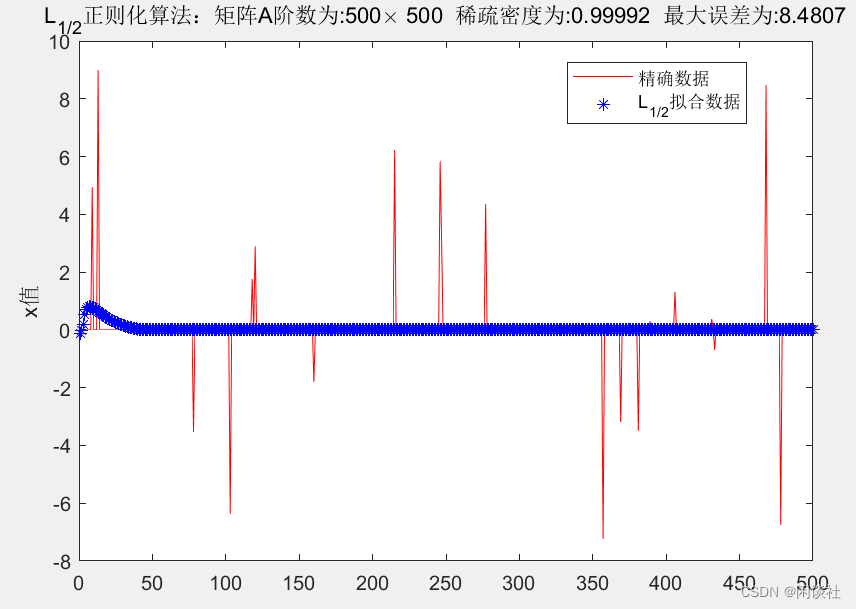
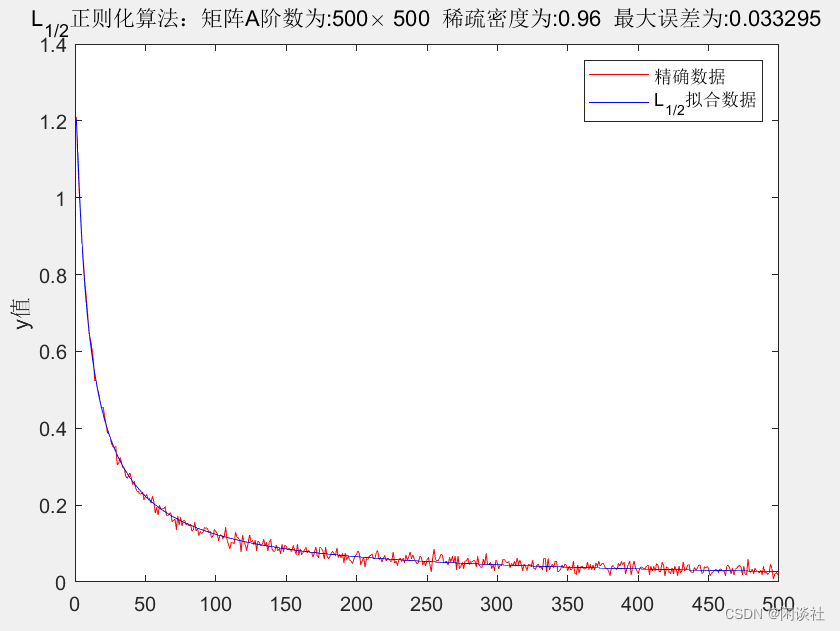
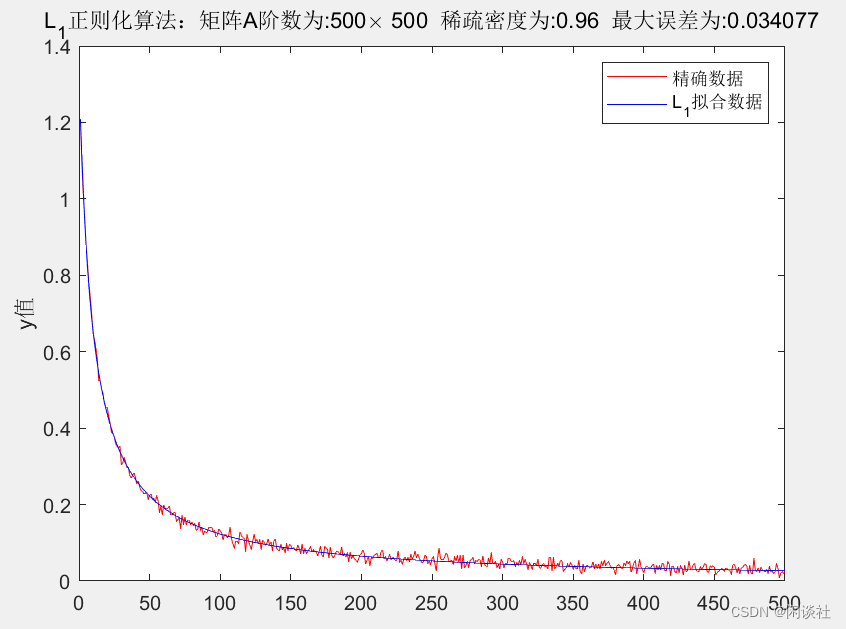
Hilbert矩阵下的高维稀疏数据反演，不论是$L_1$正则化还是$L_{1/2}$正则化，得到的结果均不理想，不能将原数据$\mathbf{x}$的稀疏性表现出来，而是将其磨光。但从观测数据$\mathbf{y}$上分析，虽然拟合的$\mathbf{y}$也被磨光处理，但依旧能较好的拟合真实数据。

经过多次尝试发现，Hilbert矩阵下的高维稀疏数据逼近模型，即$A\mathbf{x}=\mathbf{y}$，对于固定的A和$\mathbf{y}$，其解$\mathbf{x}$不唯一。

这是因为Hilbert矩阵的特征值矩阵高度稀疏，当$\mathbf{x}$也是稀疏数据，运算时将会丢失很多关键信息，因此无法正确反演稀疏数据$\mathbf{x}$。以16位有限数字为界，则$500\times 500$的Hilbert矩阵，其特征值矩阵的稀疏密度为93%。