剑指Offer——重建二叉树

题目链接

https://www.nowcoder.com/practice/8a19cbe57394eeaac2f6ea9b0f6fcf6?tpId=13&tqId=11157&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking

 

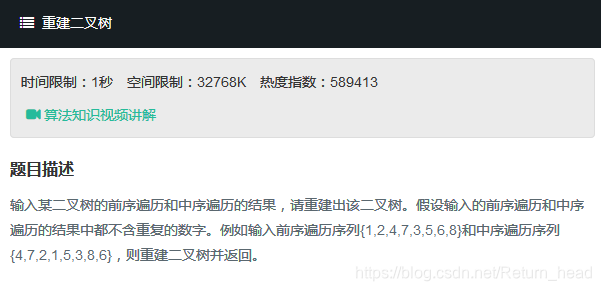
题目

函数接口

 

题解

对于该题。只要是接触过数据结构的同学，整理出思路可能并不算困难。

中序遍历是解题的关键，因为中序遍历是通过左、根、右的方式来遍历二叉树的。所以只要得到根节点，就能很快的划分出左右子树。

以本题为例。[ 4，7，2，1，5，3，8，6 ]是该二叉树的中序遍历结果。

利用前序遍历结果[1，2，4，7，3，5，6，8]，不难得出整个树的根，也即前序遍历首项为1。

从而将整个中序遍历结果又划分成两个部分。

左子树中序遍历结果[ 4，7，2 ]

和

右子树中序遍历结果[ 5，3，8，6 ]

相应的，前序遍历结果也能划分成两个部分。

左子树前序遍历结果[ 2，4，7 ]

和

右子数前序遍历结果[ 3，5，6，8 ]

由此不难对左右子树进行重建。

可见，重建二叉树的过程是一个递归的过程，即不断的通过中序和前序遍历结果重建当前的树，通过当前树的根节点将中序遍历和前序遍历结果划分成左右子树的前序、中序遍历结果，再依次对左右子树进行重建。

这里需要自定义一个方法，用于二叉树重建。

 public TreeNode reConstructBinaryTree(int pre[], int startPre, int endPre,
            int in[], int startIn, int endIn) {}

其中各个参数的意义分别为

pre[ ] —— 当前二叉树的前序遍历数组

startPre —— 当前二叉树的前序遍历数组起始索引

endPre —— 当前二叉树的前序遍历数组结束索引

in[ ] —— 当前二叉树的中序遍历数组

startIn —— 当前二叉树的中序遍历数组起始索引

endIn —— 当前二叉树的中序遍历数组结束索引

在这个方法里需要实现的功能是

1.判断该树是否为空树

2.生成TreeNode，并为val赋值

3.根据中序遍历结果和前序遍历结果，划分二叉树。并通过对划分结果进行递归，找出TreeNode的left和right(左右子树)

这里先给出伪代码

/*
 * 二叉树重建方法
 * 
 * int pre[], int startPre, int endPre三个参数
 * 其实表示的是该树中序遍历的所存的数组，故简写为PT[](Preorder traversal array)
 * 同理将int in[], int startIn, int endIn
 * 简写为IT[](Inorder Traversal Array)
 * 并引出以下几个约定
 * LPT[](Left subtree preorder traversal array)
 * LIT[](Left subtree inorder traversal array)
 * RPT[](Right subtree preorder traversal array)
 * RIT[](Right subtree inorder traversal array)
 * */	
public TreeNode reConstructBinaryTree(int pre[], int startPre, int endPre,
            int in[], int startIn, int endIn) {
    if PT[].length == 0 or IT[].length == 0
        return null
    endif
    
    TreeNode root = new TreeNode();
    root.val = pre[startPre];
	 
    for i = startIn to endIn : step=1
        if i == root.val
            root.left = reConstructBinaryTree(LPT[],LIT[]);
            root.right = reConstructBinaryTree(RPT[],RIT[]);
        endif
    endfor

    return root;
}

下面给出代码实现

p.s. 尝试加了些注释，不过不是很规范hiahiahia

public class Solution {
   /**
    * Rebuild the binary tree method
    * 
    * @param pre
    *            Preorder traversal array
    * @param in
    *            Inorder traversal array
    * @return Rebuild the binary tree root node 
    * if the returned value is <code>null</code> 
    * maybe the pre array or in array for binary tree does not exist
    */
    public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
        if (pre == null || in == null)
            return null;
        else
            return reConstructBinaryTree(pre, 0, pre.length - 1,
                    in, 0, in.length - 1);
	}

    /**
     * Rebuild the binary tree method
     * <p>
     * Rebuild the binary tree in recursive form Find the root node according to
     * the result of preorder traversal. The left and right subtrees are split
     * by the root node in the position of the inorder traversal array And
     * assign the root nodes of the left and right trees to the right and left
     * subtrees of the current node in recursive form
     * 
     * @param pre
     *            Preorder traversal array
     * @param startPre
     *            the starting index for preorder traversal array
     * @param endPre
     *            the ending index for preorder traversal array
     * @param in
     *            Inorder traversal array
     * @param startIn
     *            the starting index for Inorder traversal array
     * @param endIn
     *            the ending index for Inorder traversal array
     * @return Rebuild the binary tree root node
     */
    public TreeNode reConstructBinaryTree(int pre[], int startPre, int endPre,
            int in[], int startIn, int endIn) {

        /* returned null if the index is out of range */
        if (startPre > endPre || startIn > endIn)
            return null;

        /*
         * The preorder traversal start index is the root node of the current
         * tree
         */
        TreeNode root = new TreeNode(pre[startPre]);

        /*
         * The left and right subtrees are distinguished by the index for the
         * in-order traversal of the root node
         */
        for (int i = startIn; i <= endIn; i++) {
            /* Rebuild the left and right subtrees in recursive form */
            if (in[i] == root.val) {
                root.left = reConstructBinaryTree(pre, startPre + 1,
                                startPre + i - startIn, in, startIn, i - 1);
                root.right = reConstructBinaryTree(pre, startPre + i - startIn + 1, 
                                endPre, in, i + 1, endIn);
            }
        }
        return root;
    }
}

以上代码是通过二叉树前序遍历和二叉树中序遍历结果来重建二叉树，当然也很容易修改为通过中序遍历和后序遍历结果重建二叉树。

简单叙述下思路。

其他操作不变，因为后序遍历的结果是左、右、根，所以根节点的位置是在数组末尾。因此在利用for循环遍历后序数组时。从后往前遍历。

并相应的修改递归调用两个函数的参数值即可。

但是需要注意是已知前序、中序或者已知后序、中序结果可以重建出唯一的二叉树，但已知前序、后序遍历结果并不能得出唯一的二叉树。

 

以上是笔者对于该题的思路，如果有更好的思路或想法。可以在评论区中分享给笔者。

如果文章内容有任何问题，也欢迎指正。

最后思索一番还是给一个无注释版本的代码，如下

public class Solution {
    public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
        if (pre == null || in == null) return null;
        else return reConstructBinaryTree(pre, 0, pre.length - 1, in, 0, in.length - 1);
    }

    public TreeNode reConstructBinaryTree(int pre[], int startPre, int endPre, int in[], int startIn, int endIn) {
        if (startPre > endPre || startIn > endIn) return null;
        TreeNode root = new TreeNode(pre[startPre]);
        for (int i = startIn; i <= endIn; i++) {
            if (in[i] == root.val) {
                root.left = reConstructBinaryTree(pre, startPre + 1, startPre + i - startIn, in, startIn, i - 1);
                root.right = reConstructBinaryTree(pre, startPre + i - startIn + 1, endPre, in, i + 1, endIn);
            }
        }
        return root;
    }
}