离散傅里叶变换详解-优快云博客

本文链接：https://blog.youkuaiyun.com/ResumeProject/article/details/108279416

本文详细解析了离散傅里叶变换(DFT)的基本原理，包括序列的DFT公式，迭代次数的计算，对偶节点的概念及其计算方式，加权系数的确定方法，以及最终结果的重排序算法。通过实例说明，帮助读者深入理解DFT的运算过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

$对于一个有限长序列{xn∣0≤n≤N−1}序列的离散傅里叶变换对于一个有限长序列\{x_n| 0 \leq n \leq N-1\}序列的离散傅里叶变换$

$X(m)=∑n=0N−1x(n)e−j2πNmn=∑n=0N−1x(n)WmnX(m)=\sum_{n=0}^{N-1}x(n)e^{-\frac{j 2\pi}{N}mn}=\sum_{n=0}^{N-1}x(n) W^{mn}$
$W为N次单位根\tiny W为N次单位根$

假设N=8，则有
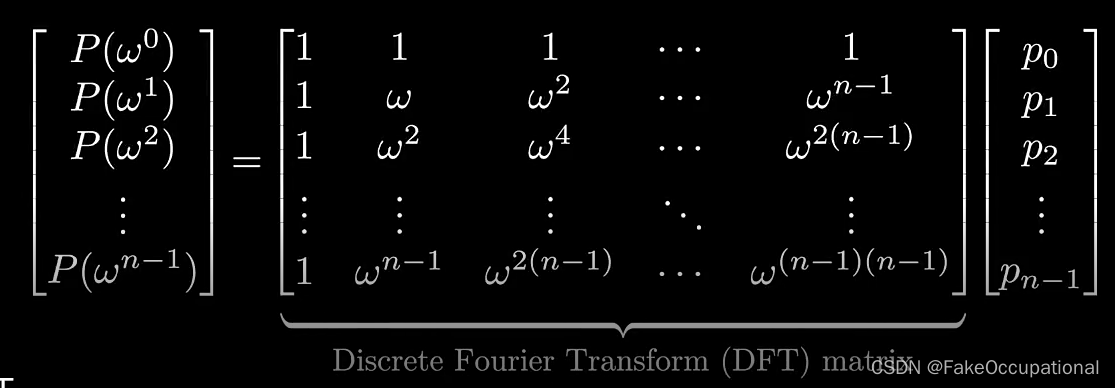
在这里插入图片描述

1.迭代次数
$r=log_2N$
2.对偶节点
$对偶节点是具有相同来源的一对节点xl(k)为第l次迭代，第k行的数据，其对偶节点为xl(k+N2l)对偶节点是具有相同来源的一对节点\\ x_l(k)为第l次迭代，第k行的数据，其对偶节点为\\ x_l(k+\frac{N}{2^l})$

$例：N=8时，x1(1)的对偶节点为x1(1+4)x2(1)的对偶节点为x2(1+2)例：N=8时，x_1(1)的对偶节点为x_1(1+4)\\ \quad \quad \quad \quad \quad \quad \quad x_2(1)的对偶节点为x_2(1+2)\\$

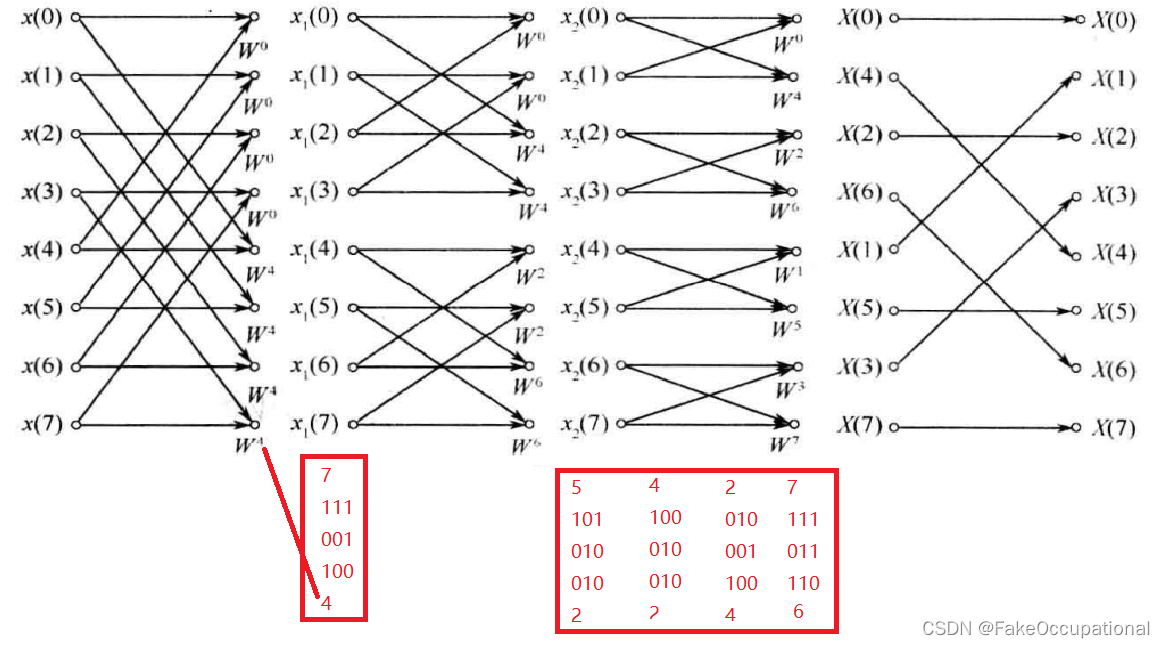
3.加权系数
$xl(k)的加权系数WNP的P值计算(本例N=8，或者说WP的计算)k写成r位二进制数，右移（r−l）位并在左侧补零，颠倒，转十进制x_l(k)的加权系数W_N^P的P值计算(本例N=8，或者说W^P的计算)\\ k写成r位二进制数，右移（r-l）位并在左侧补零，{\color{red}颠倒}，转十进制$

4.得到第r次结果的重排序
$xr(k)的k,k写成r位二进制数,颠倒，转十进制x_r(k)的k,k写成r位二进制数,{\color{red}颠倒}，转十进制$

在这里插入图片描述
$另一种看法：（转换一下观点）左到右是二对一映射,除一直线外还有一条斜线一开始以最大的跨度进行链接即，当前+N2直到最小跨度停止，即，当前+NN并且保持每次对半分割。另一种看法：（转换一下观点）\\ 左到右是二对一映射,除一直线外还有一条斜线\\ 一开始以最大的跨度进行链接{\color{red}即，当前+\frac{N}{2}}\\ 直到最小跨度停止，{\color{red}即，当前+\frac{N}{N}}\\ 并且保持每次对半分割。$