考研代码简单代码题

1. 顺序表

1.1 偶数放前

线性表，顺序结构存储，且每个元素为不相等的整数。
设计把所 有奇数移动到所有偶数前边的算法
(要求时间最少，辅助空间最少)。

思路： 双指针

1.2 元素逆置

设计一个高效算法，
将顺序表 L 中所有元素逆置，
要求算法的空间复杂度为 O(1)。

1.3 元素合并

将两个有序表合并为一个新的有序顺序表，并由函数返回结果顺序表。

1.4 删除最小

从顺序表中删除具有最小值的元素(假设唯一)并由函数返回被删除元素的 值。空出的位置由最后一个元素填补。

1.5 删除x元素 M

已知长度为 n 的线性表 L 采用顺序存储结构,编写一个时间复杂度为 O(n)、空间 复杂度为 O(1)的算法,该算法删除线性表中所有值为 x 的数据元素。

思路1，用 k 记录顺序表 L 中等于 x 的元素个数,边扫描 L 边统计 k,并将不为 x 的元
素前移 k 位,最后修改 L 的长度。对应的算法如下:

解法 2:用 i 从头开始遍历顺序表 L，k 置初始 0。若 L.data[i]不等于 x，则将其存放 在 L.data[k]中，k 增 1;若 L.data[i]等于 x，则跳过继续判断下一个元素。最后顺序表 长度置为 k。对应算法如下。

1.6 删除x-y间元素

设计一个算法，从一给定的顺序表 L 中删除元素值在 x 到 y(x≤y)之间的所有元素， 要求以较高的效率来实现，空间复杂度为 O(1)。

思路 ： 为1.5 派生，唯一不同在于是否删除的判断

1.7 数组移位 M

设将 n(n>1)个整数存放在一维数组 R 中。试着设计一个在时 间复杂度和空间复杂度都尽可能高效的算法，将 R 中保存的序列循环左移 p (0<p<n)个位置，即将 R 中的数据由(x0,x1,…,xn-1 )变换为(xp, xp+1,…,xn-1,x0,x1,…,xp-1)。

eg： R = { 0 1 2 3 4 5 6 } , p =2
out : { 2 3 4 5 6 0 1 }

思路：为了不增加额外空间。
可以 步骤1：反转 reverse(R, 0 ,L-1) =>{ 6 5 4 3 2 1 0 }
步骤2：分别反转 reverse(R, 0 ,L-p-1) ，reverse(R, L-p ,L-1)
=> {2 3 4 5 6 } + {0 1}

---

2. 链表

2.1 有序链表合并I

将两个递增的有序链表合并为一个递增的有序链表。要求结果链表仍使用原 来两个链表的存储空间，不另外占用其他的存储空间。表中不允许有重复的数据。

2.2 有序链表合并II

将两个非递减的有序表合并为一个非递增的有序表。要求结果链表仍然使用 原来两个链表的存储空间，不占用另外的存储空间。表中允许有重复的数据。

2.3 有序链表交集

已知两个链表 A 和 B 分别为两个集合，其元素递增排列。请设计一个算法，
用于求出 A 与 B 的交集，并存放在 A 链表中。

2.4 有序链表差集 M

已知两个链表 A 和 B 分别表示两个集合，其元素递增排列。请设计两个算法 求出两个集合 A 和 B 的差集(即仅由在 A 中出现而不在 B 中出现的元素所构成 的集合)，并且以同样的形式存储，同时返回该集合的元素个数。

2.5 单链表 L 中删除一个最小值结点

编写在带头结点的单链表 L 中删除一个最小值结点的高效率算法(假设最 小值结点是唯一的)。

2.6 单链表删除X元素

在带头结点的单链表 L 中，删除所有值为 x 的结点，并释放其空间，假设值 为 x 的结点不唯一，试编写算法实现上述操作。

2.7 单链就地逆置 M

试编写算法将带头结点的单链表就地逆置，所谓“就地”是辅助空间复杂度为 O(1)。

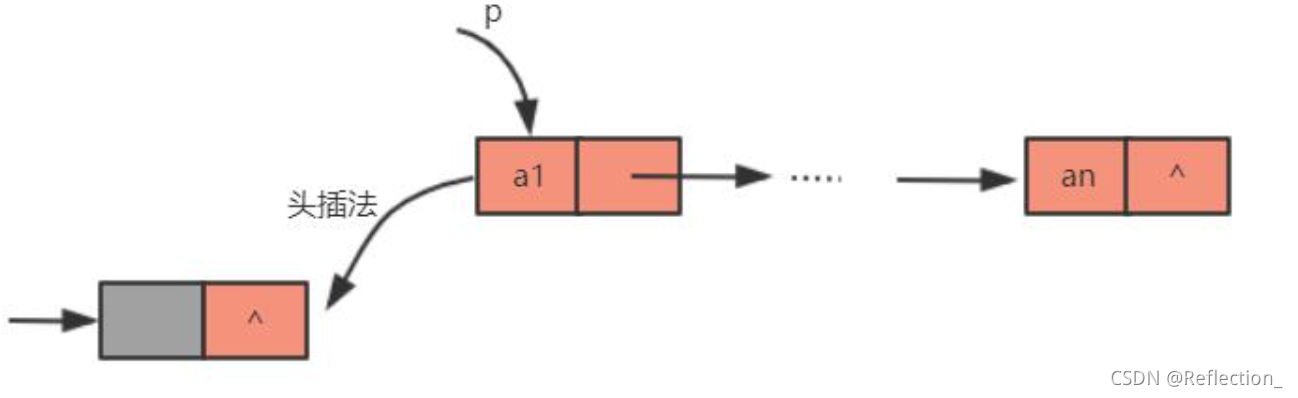
思路：将头结点摘下，然后从第一结点开始，一次插入到头结点的后面(头 插法建立单链表)，直到最后一个结点为止，这样就实现了链表的逆置，如下图 所示。

2.8 奇偶分链

将一个带头结点的单链表 A 分解为两个带头结点的单链表 A 和 B，使得 A 表 中中含有原标中序号为奇数的元素，而 B 表中含有原表中序号为偶数的元素， 且保持其相对顺序不变。

2.9 交替分链

设 C = {a1，b1，a2，b2，…，an，bn}为线性表，采用头结点的 hc 单链表存放， 设计一个就地算法，将其拆分为两个单链表，使得 A = {a1，a2，…，an}，B = {bn，…， b2，b1}。

2.10 正负分链

设计算法将一个带头结点的单链表 A 分解为两个具有相同结构的链表 B 和 C，其中 B 表的结点为 A 表中小于零的结点，而 C 表中的结点为 A 表中值大于 零的结点(链表 A 中的元素为非零整数，要求 B、C 表利用 A 表的结点)。

【变式例题】

设有一个带头结点的单链表，设计一个算法:

void split(LinkList *hc, LinkList *&ha, LinkList *&hb, ElmeType x, ElemType x)

将 hc 拆分为两个带头结点的单链表 ha 和 hb，其中 ha 的所有结点值均大于等于 x 且小于等于 y，hb 为其他结点。

2.11 单链最大元素

设计一个算法，通过一趟遍历确定长度为 n 的单链表中值最大的结点，返回 该结点的数据域。

【思路】： 指针 pmax 记录值最大的结点的 位置

2.12 删除mink-maxk间元素

设计一个算法，删除递增有序表中值大于 mink 且小于 maxk(mink 和 maxk 是给定的两个参数，其值可以和表中的元素相同，也可以不同)的所有元素。

2.13 去掉重复元素

在一个递增有序的线性表中，有数值相同的元素存在。若存储方式为单链表，
设计算法去掉数值相同的元素，使表中不再具有重复的元素。

2.14 元素分类

已知由单链表表示的线性表中,含有 3 类字符的数据元素(如:字母字符、数字 字符和其他字符),试编写算法构造 3 个以循环链表表示的线性表,使每个表中只含 同一类的字符,且利用原表中的节点空间作为这三个表的节点空间,头节点可另辟 空间。

【思路】 带头循环链表 可用头插入法

2.15 判断

已知带头节点的循环单链表 L 中至少有两个节点,每个节点的两个字段为 data 和 next,其中 data 的类型为整型。试设计一个算法判断该链表中每个元素的 值是否小于其后续两个节点的值之和。若满足,则返回 true;否则返回 false。

【注意】 带头循环链表 的遍历