像素处理
像素处理会对图像中每一个像素做出函数转换
- 阈值(threshold)处理 - 可以通过设置像素值来创建掩模(mask)为 1 或 0,具体取决于当前值是否高于或低于某个阈值。
- 色彩校正 - 可以修改图像以增加或降低对比度(contrast)或亮度(brightness)。
- 补充图像
• 类别:图像增强/恢复
• 实现:O(x,y) = 255 - I(x,y)

对比度调整
- 线性拉伸(linear stretching)

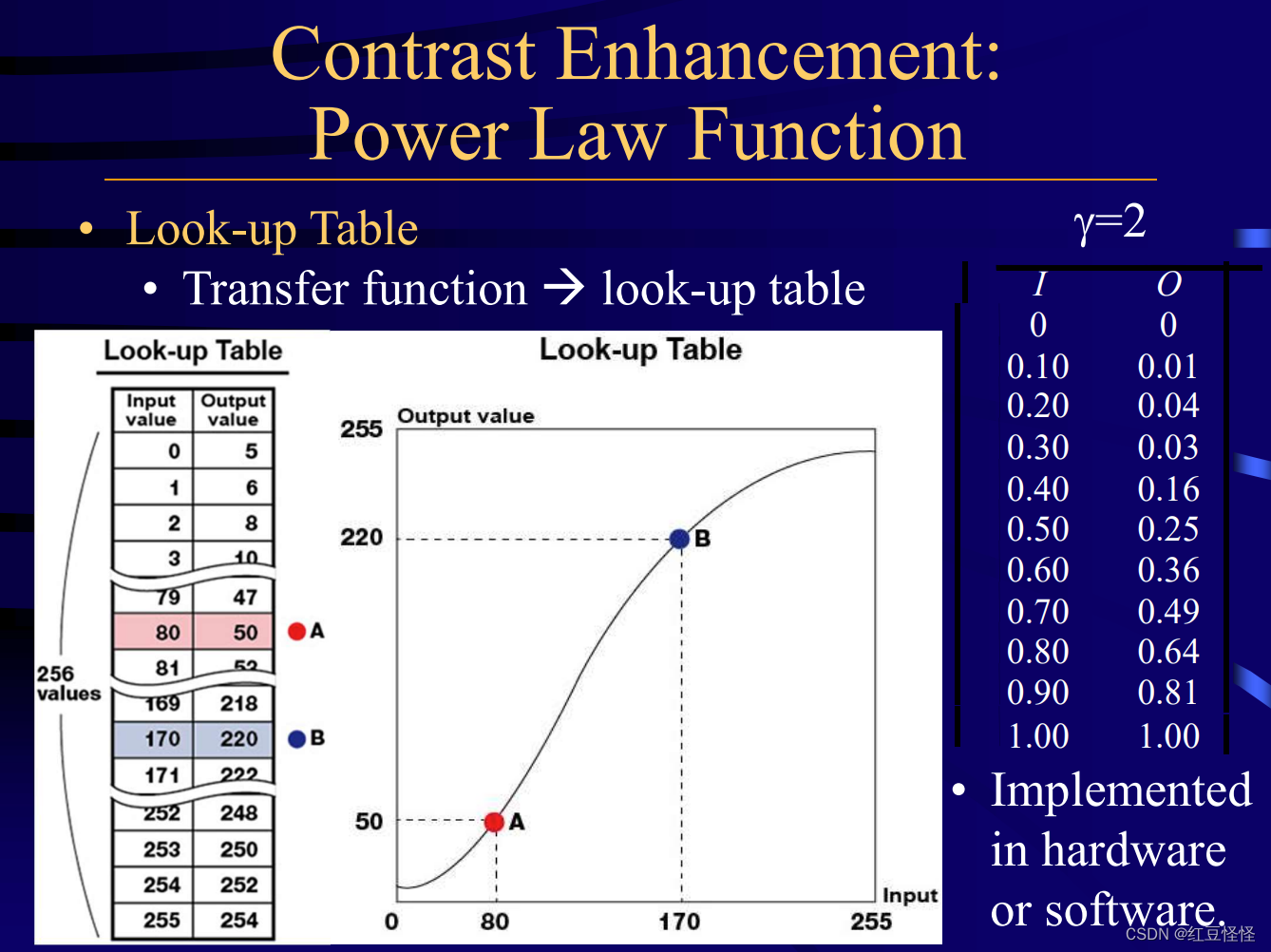
- 幂律函数转换(Power Law function)
O=IγO = I^\gammaO=Iγ
• γ<1\gamma < 1γ<1 在暗的地方增加对比度
• γ>1\gamma > 1γ>1 在亮的地方减少对比度
一般先正则化亮度值,如除以256使之在(0, 1)之间。再待入函数中。
这种方法在实践中常常使用查询表直接转换。
- 对比度增强:直方图均衡(histogram Equalisation)
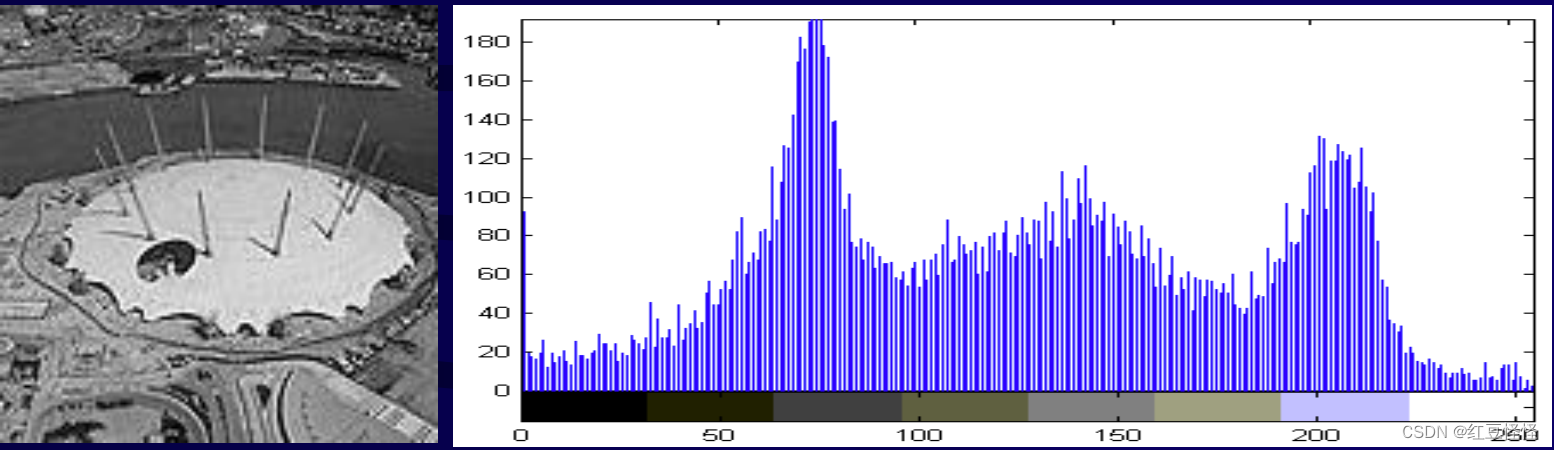
- 图像直方图
显示图像像素的灰度分布。
• 灰度级 j=0,1,…,255
• Nj = 图像中灰度级为 j 的像素数
• Nj 与 j 的关系图
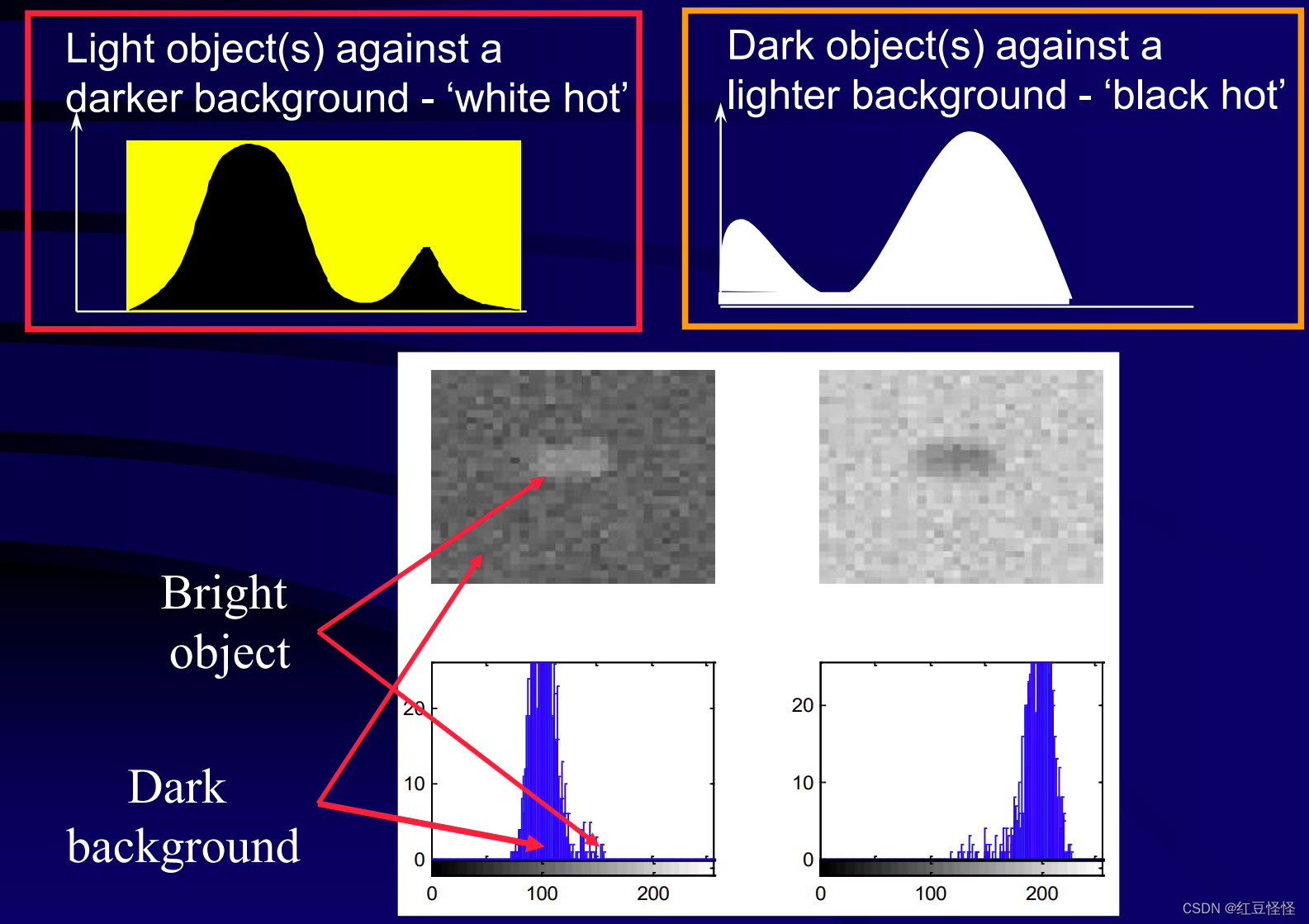
双峰直方图

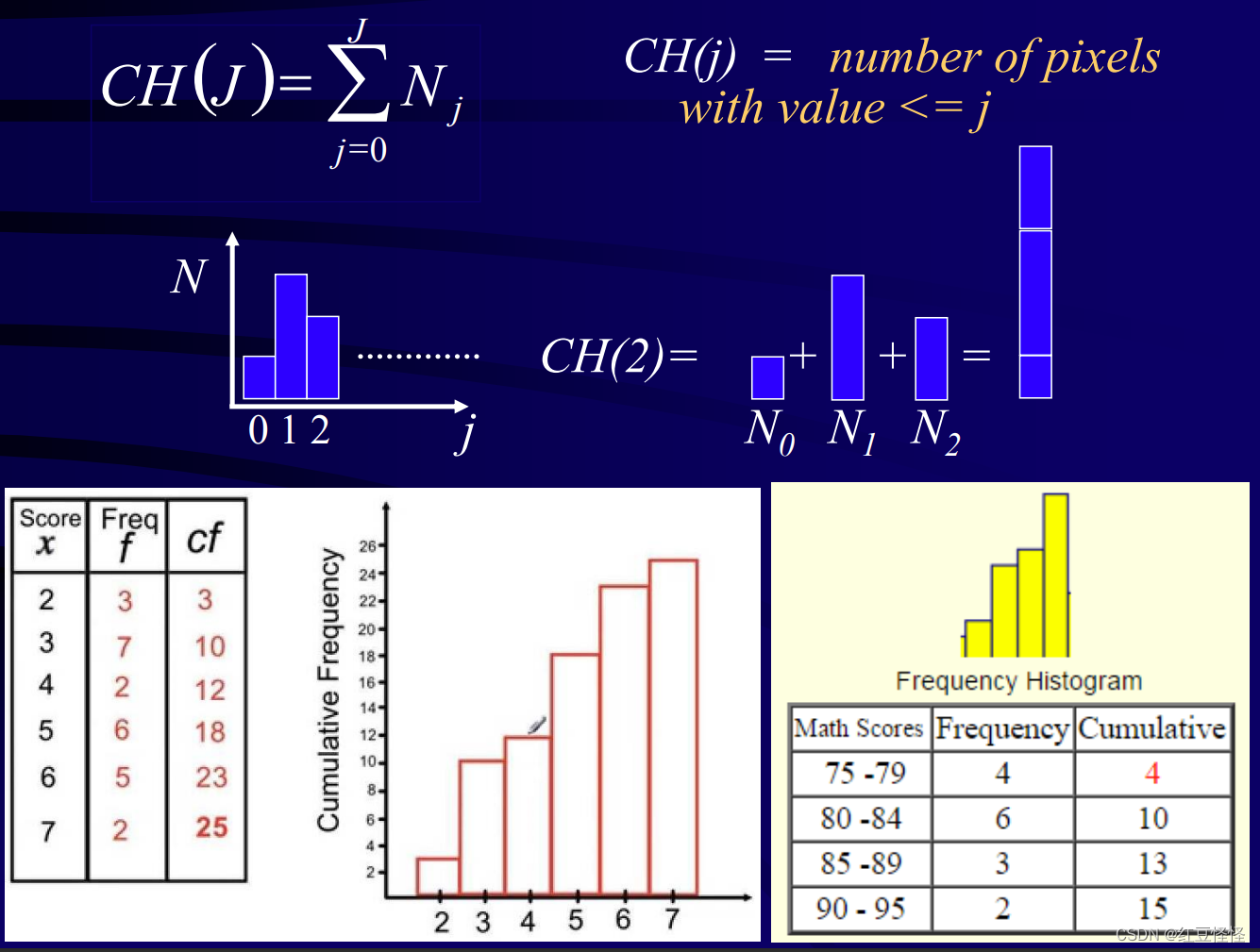
累计直方图
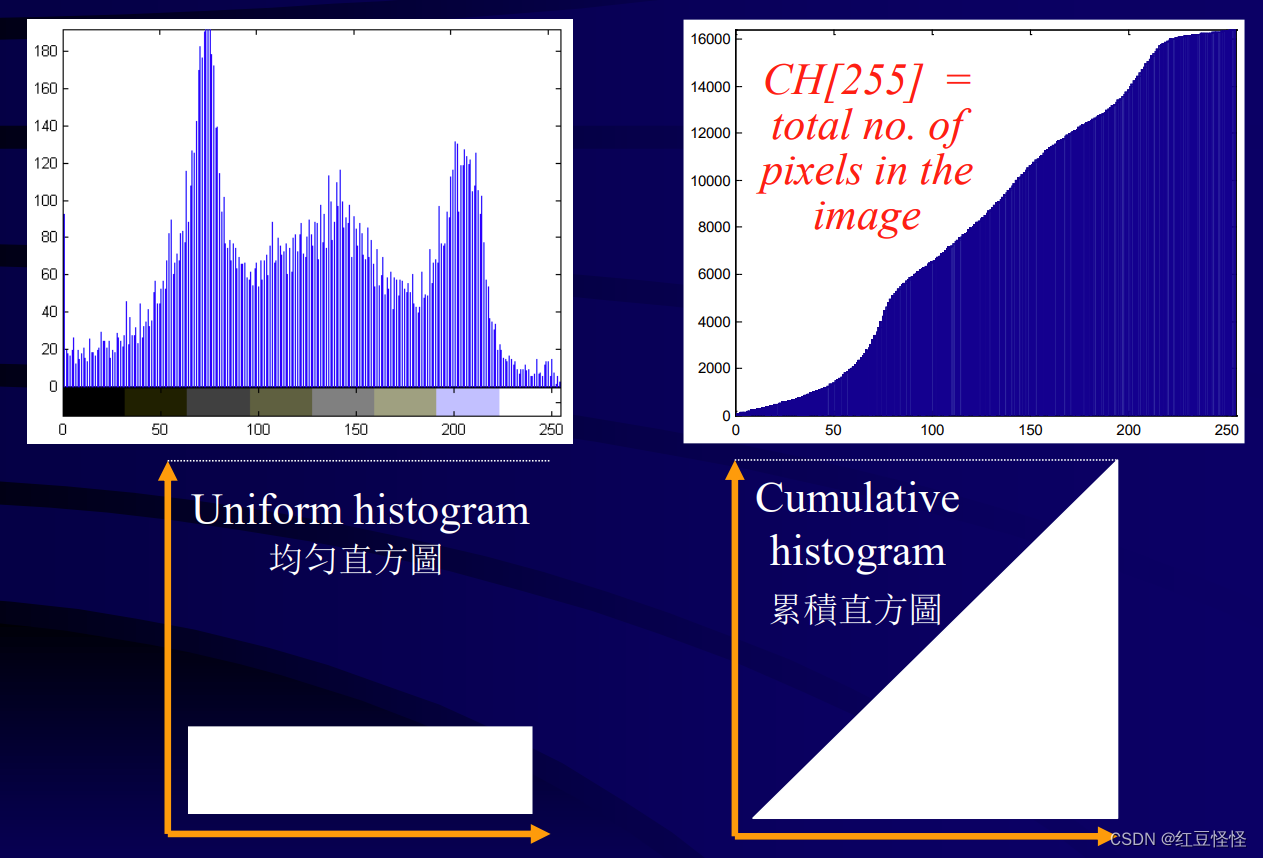
灰度均匀分布的图像的累积直方图是一条直线
由峰值(peak)和低平原(low plain)组成的图像直方图。
• 峰值 = 许多像素集中在几个灰度级中
• 平原 = 分布在更广泛的灰度级上的少量像素
我们希望将峰值中的像素扩展到更广泛的灰度级。
• 将低平原像素“压缩”到更窄的灰度级范围内。
• 最终得到较平坦的直方图。
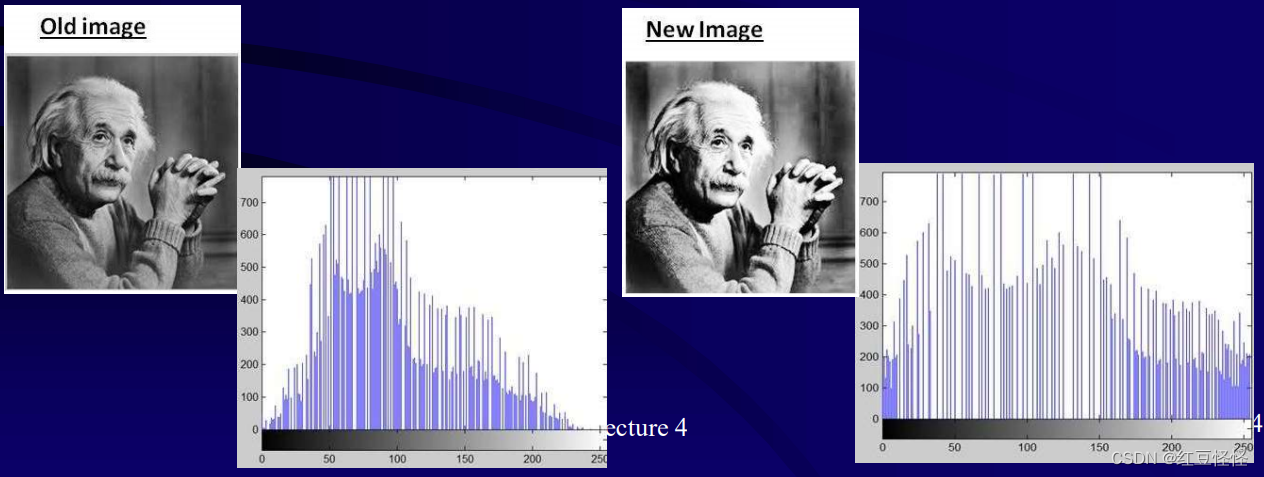
从一组灰度级 j 映射到一组新的灰度级 i。
公式:
Np=M×NGN_p = \frac{M \times N}{G}Np=GM×N
i=MAX{0,round(CH(j)Np)}i = MAX\{ 0, round(\frac{CH(j)}{N_p}) \}i=MAX{0,round(NpCH(j))}
注:M,N为像素行数,列数,round 指四舍五入函数。CH(j)指到第j组像素集以来像素的总和,G指我们想要重新分的像素的组数。下面是一个例子:
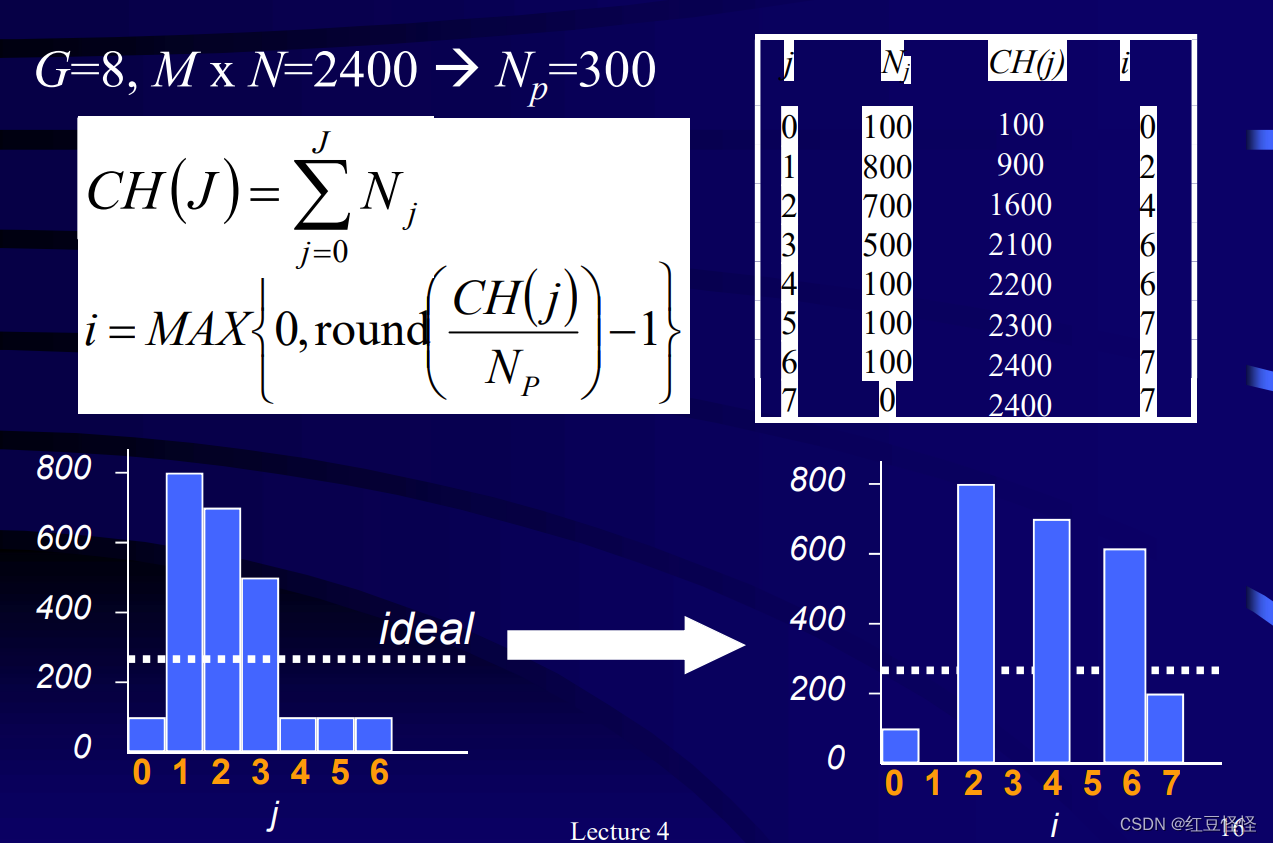
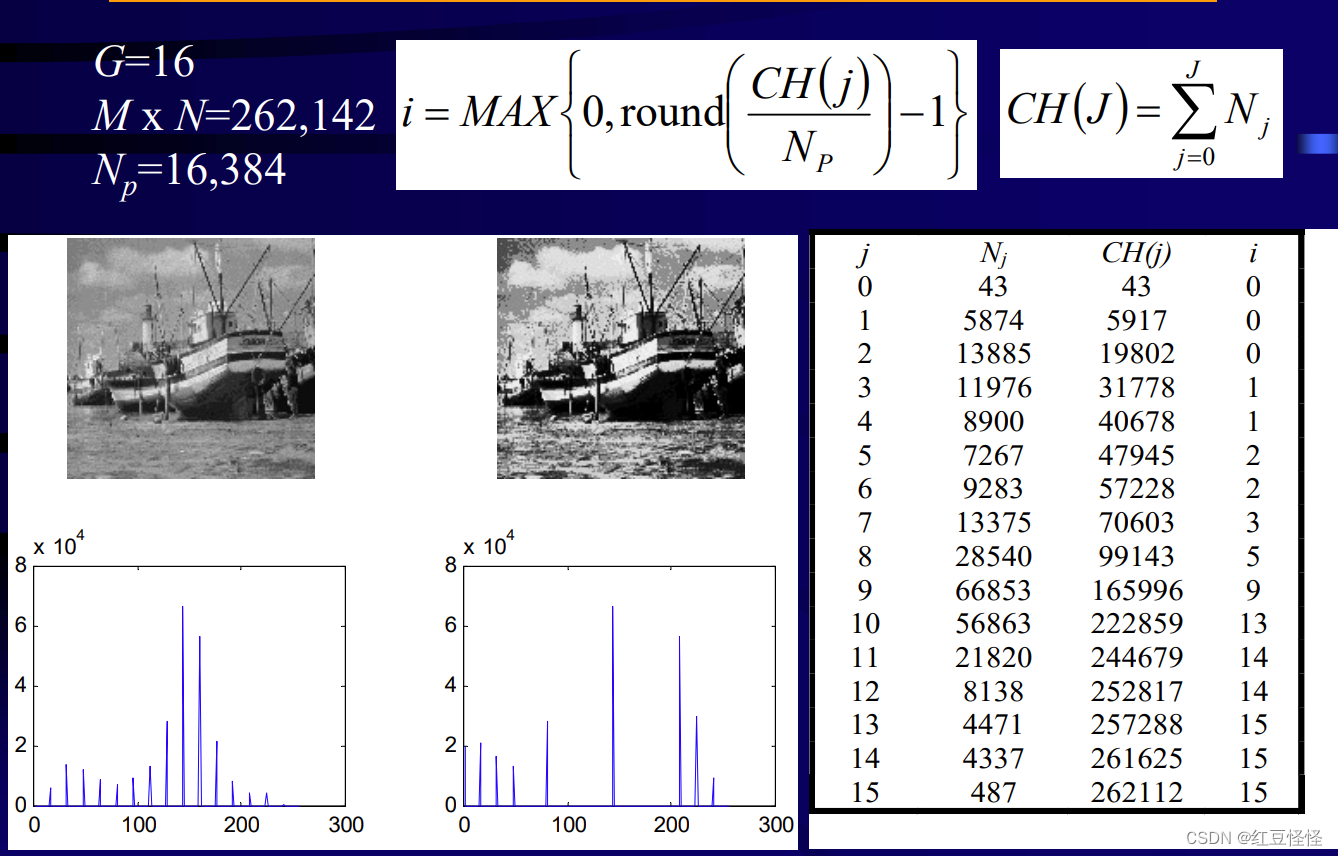

近邻操作
为什么邻接像素很重要?
- 为各个像素提供上下文(context)。
- 邻接像素之间的关系决定图像特征。
- 卷积(Convolution)
- 包括使用过滤器(掩模)B 对图像 A 进行过滤。
- 掩模是一个小图像,其像素值称为权重(weight)。
- 权重修改像素之间的关系。
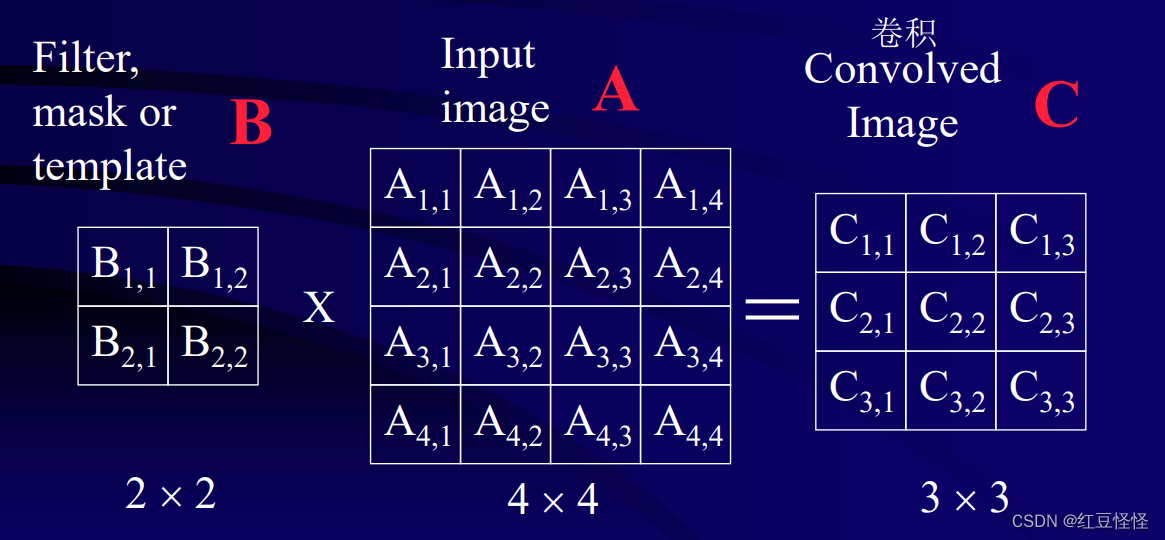

卷积尺寸
图像尺寸: M_1 ×\times× N_1
mask尺寸: M_2×\times× N_2
卷积尺寸: M_1- M_2+1 ×\times× N_1 - N_2 + 1
噪音(noise)
噪声源 = CCD 芯片
• 检测器中的电子信号波动(fluctuation)。
• 由热能(thermal energy)引起。
• 对于红外(intra red)传感器来说情况更糟。
图像亮度图。
• 垂直切片图像。
• 噪声是累加性的。
• 噪声波动快速,即频率高。
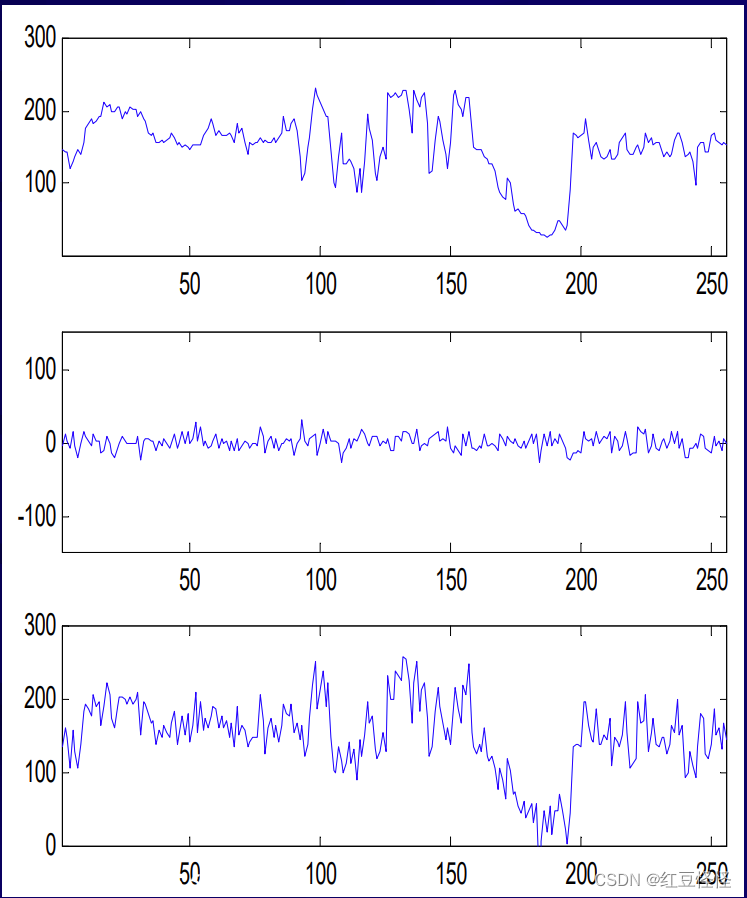
- 减少噪音的第一定律
我们如何减少噪音?
- 考虑均匀的一维图像A 并添加噪声。
- 关注像素邻域。
- 中心像素增加,相邻像素减少
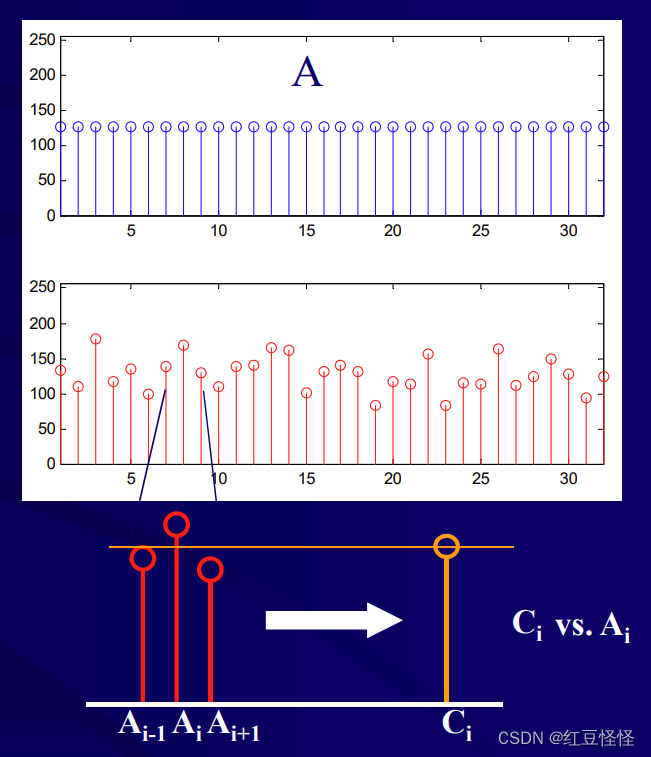
- 平均可以“平滑”噪声波动。Ci=Ai−1+Ai+Ai+13C_i = \frac{A_{i-1}+A_{i} + A_{i+1}}{3}Ci=3Ai−1+Ai+Ai+1
- 考虑下一个像素Ai+1A_{i+1}Ai+1
- 对剩下的像素重复该操作。
- 用于降噪的低通滤波器(Low Pass Fliter)
通过将一维图像 A 与掩模 B 进行卷积,可以对所有像素进行平均,得到增强的图像 C。 加在一起时,B 的权重必须等于 1。
例如,第一定律可以被认为是一种特殊的Low Pass Filter

拓展到二维:
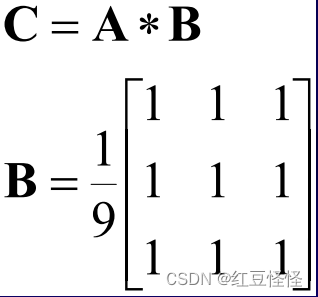
- 过滤的设计
过滤涉及将函数应用于图像或选择中的每个像素,但该函数不仅利用像素的当前值,还利用相邻像素的值。 一些过滤功能:
- blur(模糊)
- sharpen(锐化)
- soften (软化)
- distort(歪曲)
技术依赖于“阻止”高频噪声波动通过过滤器。 因此,在低通滤波器中。
• 图像中的精细细节也可能会被平滑。
• 保持图像精细细节和减少噪点之间的平衡。
• 例子:
– 土星图像粗糙细节
– 船图像包含精细的细节
– 噪点减少,但细节也被平滑化(smoothed)
- 低通过滤的问题
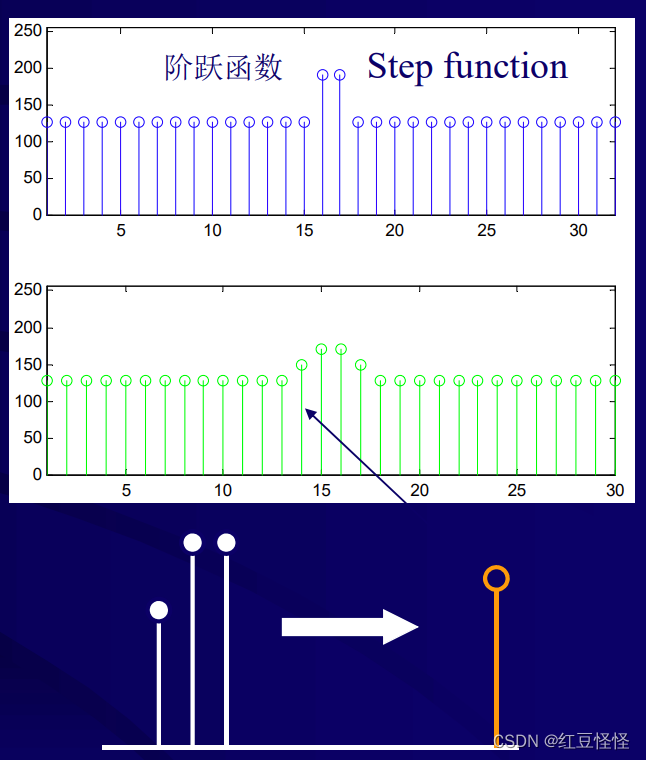
考虑具有阶跃函数的均匀一维图像 A。
• 阶跃函数对应于精细的图像细节,例如边缘。
• 低通滤波器“模糊”边缘。
- 用于降噪的中值滤波器
我们如何在不平均的情况下减少噪音?
• 考虑均匀的一维图像A 并添加噪声。
• 关注像素邻域。
• 非线性算子?
中值滤波器!在三个值中取中位数而不是平均数。
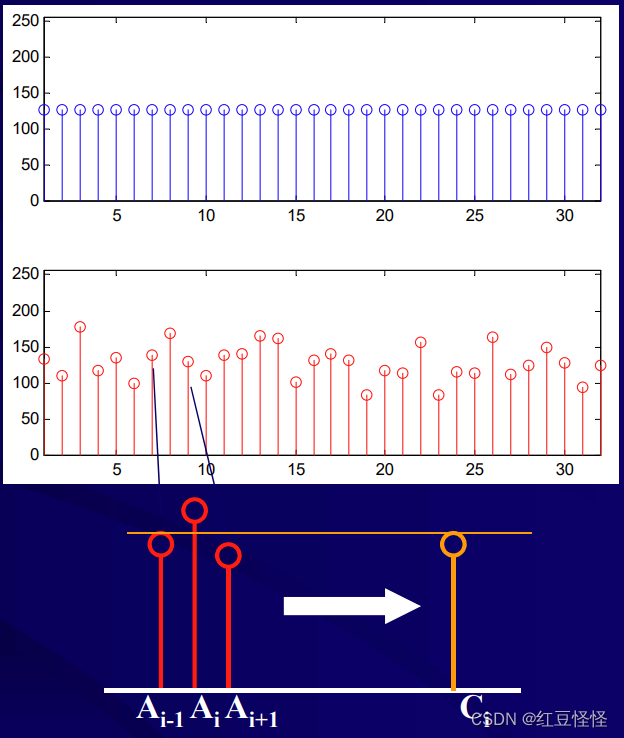
通过将一维图像 A 与中值滤波器 B 进行卷积,可以将所有像素替换为邻域中值,从而得到增强的图像 C。
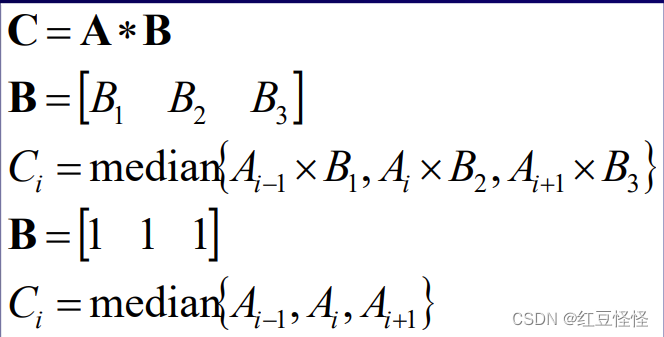
例子:

总结:
• 低通:通过平均平滑精细细节;
• 中值:通过过滤器的精细细节。
过滤操作
上面提及了低通过滤
- 低通滤波器
• 类别:用于图像增强/恢复
• 应用:像素组处理和平滑图像
1 1 1 | 1 1 1 |1 2 1
1 1 1 | 1 2 1 |2 4 2
1 1 1 | 1 1 1 |1 2 1
/9 /10 /16
特征:和为1
2. 高通滤波器
应用:像素组处理并锐化图像
1 -1 -1 | 0 -1 0 | 1 -2 1
-1 9 -1 |-1 5 -1 | -2 5 -2
-1 -1 -1 | 0 -1 0 |1 -2 1

特征相加和为1;
索贝尔边缘增强
• 应用:边缘提取
-1 0 1 | -1 -2 -1
-2 0 2 | 0 0 0
-1 0 1 | 1 2 1
Vertical mask Horizontal mask

拉普拉斯边缘增强
• 实施:全边缘提取
1 -1 -1 | 0 -1 0 | 1 -2 1
-1 8 -1 | -1 4 -1 | -2 4 -2
-1 -1 -1 | 0 -1 0 | 1 -2 1


总结
图像处理:
– 点(像素)操作;
– 邻里运营
• 点操作
– 亮度和对比度增强,因为采集过程会降低图像质量;
– 方法:线性拉伸、幂律函数和直方图均衡
• 邻里运营
– 降噪和边缘增强;
– 方法:低通滤波器、中值滤波器、高通滤波器




 本文介绍了像素处理中的各种技术,如阈值处理、色彩校正(包括对比度和亮度调整)、线性拉伸与幂律函数转换,以及直方图均衡用于对比度增强。还讨论了降噪方法如低通滤波(如平滑效果)和中值滤波(非线性处理),以及边缘增强技术如高通滤波和边缘检测滤波器的应用。
本文介绍了像素处理中的各种技术,如阈值处理、色彩校正(包括对比度和亮度调整)、线性拉伸与幂律函数转换,以及直方图均衡用于对比度增强。还讨论了降噪方法如低通滤波(如平滑效果)和中值滤波(非线性处理),以及边缘增强技术如高通滤波和边缘检测滤波器的应用。

















 10万+
10万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










