项目场景:
提示:这里简述项目相关背景:
压实度(Evd)是指土体在压实作用下的密实程度,是衡量路基工程质量的重要指标之一。压实计值(CMV)是一种基于电磁波原理的无损检测方法,可以实时反映路基压实情况。压实度(Evd)与压实计值(CMV)之间的关系是影响路基质量控制的关键因素,但目前还没有形成统一的理论和方法。
问题描述
提示:这里描述项目中遇到的问题:
本文基于已采样的318组数据,经过傅里叶变换进行频域分析得到其对应的压实计值(CMV)。针对这318组离散数据,作者采用了多项式回归、非线性回归、非负最小二乘法(NNLS)、基于高斯核函数的SVM模型等多种回归模型来拟合。
为了评估模型准确性,我以误差平方和的平方根(RMSE)为标准计算各个模型的值。最终,表现最好的是一个SVM模型——GSVM。它是以采用高斯核函数的支持向量机为预训练模型,经过233轮迭代训练得到的。该模型的误差值相对较小,在一定程度上能反映压实计值与压实度(Evd)二者之间的关系。
数据分析:
提示:这里填写问题的分析:
文利用采集到的318组数据,每个文件中各个数据采样间隔为1s,长度大多数为1024.存放数据的每个文本文件名为采样地点的压实度(Evd)
傅里叶频域分析
傅里叶频域分析是一种数学方法,用于将一个信号分解为不同频率的正弦波和余弦波的组合。这种分析可以帮助我们了解信号的特征,如频率、幅度、相位等。本文使用python3里numpy库中的’.fft’函数对所有318个文件中的数据分别进行傅里叶变换,并存于新的文本文件中
计算压实计值(CMV)
将上述得到的处理过的数据依照如下公式计算压实计值,即可得到CMV:
# 导入模块
import os
import numpy as np
# 定义文件夹路径和输出文件路径
folder = "data" # 你的文件夹路径
output = "result2.txt" # 你的输出文件路径
# 获取文件夹中所有文件的列表
files = os.listdir(folder) # 返回一个列表,包含文件夹中所有文件的名称
# 打开输出文件
with open(output, "w") as out: # 以写的方式打开输出文件
# 遍历文件列表
for file in files: # 对每个文件
# 拼接文件的完整路径
path = os.path.join(folder, file) # 使用os.path.join函数,将文件夹路径和文件名称拼接成完整的文件路径
# 读取文件内容
data = np.loadtxt(path) # 使用numpy的loadtxt函数,将文件中的数据转换为数组
# 进行傅里叶变换
y = np.fft.fft(data) # 使用numpy的fft函数,进行傅里叶变换
# 计算幅度谱
L = len(data) # 信号长度
P = 2 * np.abs(y) / L # 使用numpy的abs函数,计算幅度谱
# 定义采样频率和信号长度
Fs = 1024 # 采样频率,根据你的实际情况修改
# 计算基频和二次谐波分量的频率
f0 = Fs / L # 基频
P_1max = np.max(P) # 基频最大值
A_1 = np.argmax(P) # 基频的序号
A_11 = 2 * A_1
t1 = A_11 - 10
t2 = A_11 + 10
P_2 = P[t1:t2] # 二次频率的域
if len(P_2) > 0:
P_2max = np.max(P_2) # 二次频幅值
A_2 = np.argmax(P_2) + t1 # 二次频幅值的序号
C = 100
CMV = C * P_2max /P_1max
# out.write(file + "\n") # 写入文件名
out.write( str(CMV) + "\n") # 写入基频的幅值
# out.write("\n") # 换行
读取Evd值
使用os库读取所有文本文件名,并生成文本文件。为了不引起歧义,在读取时,将‘xxx(2)’此类文件替换为‘xxx0’,这样做并不影响后续计算中的数值大小。通过上述步骤,我们就得到了318组代表X的CMV值和代表Y的Evd值。
# 导入os模块,用于操作文件和目录
import os
# 指定文件夹的路径,例如'C:\\test'
folder = 'F:\BENKE\JIANZAO\CMA\data'
output = "name.txt"
# 创建一个空列表,用于存储文件名
names = []
# 遍历文件夹中的所有文件
for file in os.listdir(folder):
# 判断文件是否是txt文件
if file.endswith('.txt'):
# 去掉文件的后缀名
name = os.path.splitext(file)[0]
# 将文件名添加到列表中
names.append(name)
# 打开一个新的txt文件,用于写入文件名,例如'name.txt'
with open('name.txt', 'w') as f:
# 遍历列表中的文件名
for name in names:
# 将文件名写入txt文件,并换行
f.write(name + '\n')
解决方案:
提示:这里填写该问题的具体解决方案:
1 多项式拟合
通过调用多项式拟合是一种基本的拟合方法,它使用多项式函数来逼近数据。多项式拟合可以通过最小二乘法(Least Squares Method)或使用多项式拟合函数,如numpy.polyfit函数来实现。
将CMV作为X,Evd作为Y输入,拟合该散点数据。为了更好的拟合该数据,作者需要确定不同阶数,从而选择最佳方案。在此,作者尝试2、4、6阶多项式来拟合
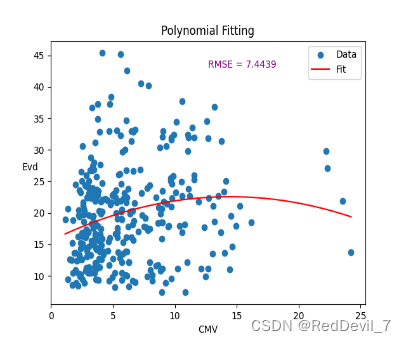
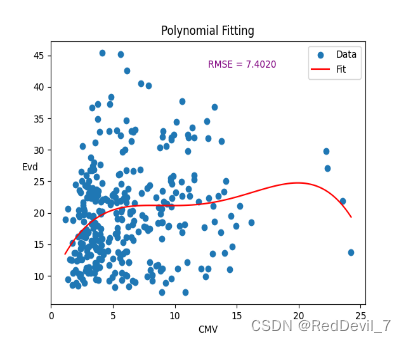
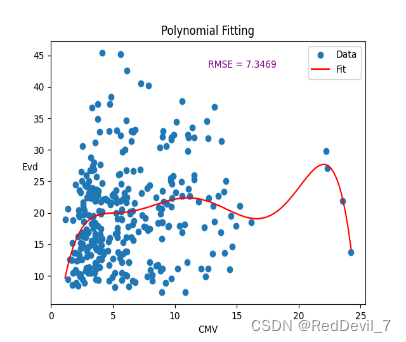
由上文可知,我们选择4阶多项式作为拟合函数。通过.coefficients函数,我们可以得到了多项式的系数,从而确定了其表达式如下:
同时,依据损失平方和的平方根公式,计算RMSE:
得到RMSE=7.4020
2 非负最小二乘
非负最小二乘(Non-negative Least Squares,NNLS):NNLS是一种用于拟合非负数据的方法,它将拟合系数约束为非负值。NNLS方法常用于信号处理、图像处理和化学分析等领域。
我们使用scipy.optimize.nnls函数进行非负最小二乘拟合,将设计矩阵X和响应变量Y_data作为输入。函数返回拟合系数coefficients和残差。
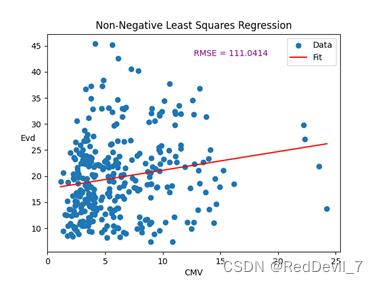
可以看到,虽然函数依旧拟合效果很差,但相对于模型二有一定改善。
依旧按照之间的方式输出系数,可以得到该方法的表达式
3 基于高斯核函数的SVM模型——GSVM
非线性分类问题是指通过利用非线性模型才能很好地进行分类的问题。对于高维数据,假设我们可以通过一个转换函数将低维空间的数据集映射到高维空间的数据集,这时候的数据会变得容易线性可分。
因此,我们引入核函数的概念。其中心思想是在学习和预测中,只定义核函数而不显式定义映射函数。只计算核函数会简化流程,其公式如下:
其中,代表了输入空间到特征空间的映射。
接下来我们再引入SVM(支持向量机),是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器,常用的核函数有多项式核函数、高斯核函数。
在这里,我们为了区别于模型一,使用高斯核函数,其表达式如下:
它对应的是高斯径向基函数,于是分类决策函数变为,
SVM的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的学习算法就是求解凸二次规划的最优化算法。
本文中,我们使用MATLAB中内置的Gaussian SVM预训练模型,将前面处理的318个CMV数据作为predictor,将Evd作为response,采用10折交叉验证来提高模型泛化能力。最终,迭代233次得到了最终的GSVM模型。
我们通过KernalScale读出该模型的kernalscale=0.1565,同时该模型逻辑收敛。
依据式(8)算出该模型的高斯函数(9),其拟合及预测效果如图
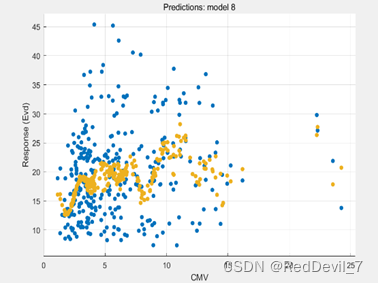
经过计算,其误差如表
| RMSE | 7.40 |
| R-Squared | 0.00 |
| MSE | 58.20 |
| MAE | 5.93 |
模型评价
模型分析
通过以上模型对比可知,采用以Gaussian kernal函数的GSVM模型具有相对强的可靠性。有可能的原因是,它在训练过程中采用交叉验证方法,保证了训练集和测试集的随机性,从而得到的特征矩阵较为具化,鲁棒性更佳。
模型改进
由于时间限制,没能进一步优化模型参数。或许可以采用的方法是,使用贝叶斯调参、网格搜索调参或者启发式搜索方法优化该模型,以实现保证泛化能力的前提下具有更高的使用价值。







 本文详细研究了通过傅里叶变换和SVM技术分析道路工程中压实度与压实计值的关联,展示了多项模型比较及高斯SVM模型在实际应用中的优势。
本文详细研究了通过傅里叶变换和SVM技术分析道路工程中压实度与压实计值的关联,展示了多项模型比较及高斯SVM模型在实际应用中的优势。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








