傅里叶级数拟合实验

最新推荐文章于 2025-04-28 12:43:44 发布

原创

最新推荐文章于 2025-04-28 12:43:44 发布 · 1.5w 阅读

30 ·

CC 4.0 BY-SA版权

文章标签：

#matplotlib #数学计算 #python

本文展示了利用Python的matplotlib库进行傅里叶级数拟合的实验，通过19项傅里叶级数对随机数据进行拟合，并生成误差分布图，结果显示效果良好，接近标准正态分布。程序主要涉及数学计算，包括傅里叶级数的方程组生成和高斯消元法求解系数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这是11月研究matplotlib的成果，顺便复习了一下高数。

下面是程序的运行结果，蓝色为随机生成的源数据，绿色为用傅里叶级数（19项）拟合的结果，效果还是蛮好的。中间上方的小图为误差分布，接近标准正态分布。

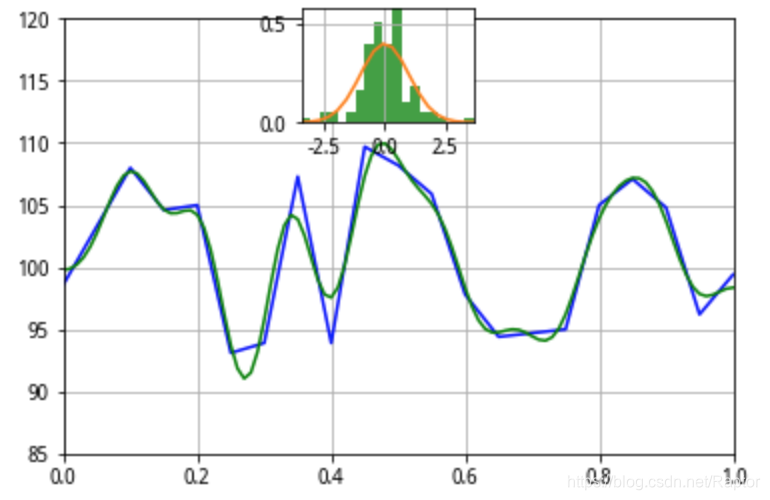
程序中比较复杂的部分都是数学计算有关的，一个是傅里叶级数展开的方程组生成——通过源数据作最小二乘拟合；另一个是用高斯消元法解这个方程组，得到傅里叶级数的系数。其它就是调用matplotlib作图了。

本程序没有什么实际意义，纯属写着玩的。^O^

以下代码可在Jupyter Notebook里运行看效果。

import matplotlib.pyplot as plt
from scipy.stats import norm
import random


def Sigma( func, size ) :
	c = 0
	for i in range(size) :
		c = c + func( i )
	return c

# ordinary least squares to Fourier级数
# Xlist and Ylist are some points
# restul is a matrix include cnSyntonicX(cnSyntonic+1) items
def ols2fourier( Xlist, Ylist, cnSyntonic ) :
	cnPoints = len( Ylist )
	line = []
	line.append( Sigma( lambda x : 0.5, cnPoints ) / 2 )
	for j in