Raki的读paper小记：Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context

Abstract&Introduction&Related Work

• 研究任务
  不受长度限制的transformer
• 已有方法和相关工作
  没有基于transformer的方法，都是基于RNN
• 面临挑战
• 创新思路
• 实验结论
  在学习依赖上优于RNN 80%，普通transformer 450%，评估速度比普通transformer快1800倍

Transformer-XL

Segment-Level Recurrence with State Reuse

在训练过程中，为前一个片段计算的隐藏状态序列是固定的，并在模型处理下一个新片段时作为扩展上下文被重新使用。

定义
$${\mathbf{s}}_{\tau }=\left[x_{\tau ,1},\cdots ,x_{\tau ,L}\right]\text{ and }{\mathbf{s}}_{\tau +1}=\left[x_{\tau +1,1},\cdots ,x_{\tau +1,L}\right]$$
隐藏层，SG代表stop-gredient
$$\begin{array}{l}{\tilde{\mathbf{h}}}_{\tau +1}^{n-1}=\left[\mathrm{SG}\left({\mathbf{h}}_{\tau }^{n-1}\right)\circ {\mathbf{h}}_{\tau +1}^{n-1}\right],\\ {\mathbf{q}}_{\tau +1}^n,{\mathbf{k}}_{\tau +1}^n,{\mathbf{v}}_{\tau +1}^n={\mathbf{h}}_{\tau +1}^{n-1}{\mathbf{W}}_q^{\top },{\tilde{\mathbf{h}}}_{\tau +1}^{n-1}{\mathbf{W}}_k^{\top },{\tilde{\mathbf{h}}}_{\tau +1}^{n-1}{\mathbf{W}}_v^{\top },\\ {\mathbf{h}}_{\tau +1}^n=\text{ Transformer-Layer }\left({\mathbf{q}}_{\tau +1}^n,{\mathbf{k}}_{\tau +1}^n,{\mathbf{v}}_{\tau +1}^n\right).\end{array}$$

普通的transformer layer：

在隐藏层创造了segment-level的循环，与RNN不同的是，这里每段向下移动一层

最大可能的依赖是图b的面积下的点，与截断的BPTT不同的是，这里的方法缓存了一连串的隐状态，而不是最后一个，因此应该与相对位置编码技术一起应用

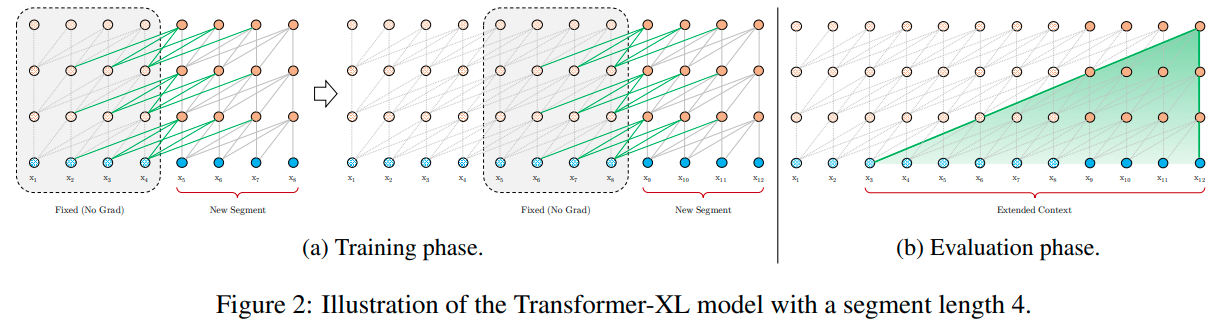
不只是前一个segment，可以与前多个segment相连

Relative Positional Encodings

当重用之前的state信息的时候，保持他们的位置信息也是非常重要的，如果依旧使用绝对位置编码，会出现两个segment用了同样的位置的情况，但实际上却差了一个segment的长度，这样会使模型无法区分他们的位置信息
$$\begin{array}{c}{\mathbf{h}}_{\tau +1}=f({\mathbf{h}}_{\tau },{\mathbf{E}}_{\tau +1}+{\mathbf{U}}_{1:L})\\ {\mathbf{h}}_{\tau }=f({\mathbf{h}}_{\tau -1},{\mathbf{E}}_{{\mathbf{s}}_{\tau }}+{\mathbf{U}}_{1:L}),\end{array}$$

绝对位置编码：
$$\begin{array}{c}{\mathbf{A}}_{i,j}^{q\text{is}}=\underset{(a)}{\underbrace{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{E}}_{x_j}}}+\underset{(b)}{\underbrace{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{U}}_j}}+\underset{(c)}{\underbrace{{\mathbf{U}}_i^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{E}}_{x_j}}}+\underset{(d)}{\underbrace{{\mathbf{U}}_i^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{U}}_j}}.\end{array}$$

相对位置编码：
把所有的 $U_j$ 都换成了 $R_{i-j}$ 一个正弦波编码矩阵
$u^{\top }$ 和 $v^{\top }$ 是可训练参数
$${\mathbf{A}}_{i,j}^{\mathrm{rel}}=\underset{(a)}{\underbrace{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_{k,E}{\mathbf{E}}_{x_j}}}+\underset{(b)}{\underbrace{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_{k,R}{\mathbf{R}}_{i-j}}}+\underset{(c)}{\underbrace{u^{\top }{\mathbf{W}}_{k,E}{\mathbf{E}}_{x_j}}}+\underset{(d)}{\underbrace{v^{\top }{\mathbf{W}}_{k,R}{\mathbf{R}}_{i-j}}}.$$

Transformer-XL的总公式
$$\begin{gathered} \begin{array}{c}{\tilde{\mathbf{h}}}_{\tau }^{n-1}=\left[\mathrm{SG}({\mathbf{m}}_{\tau }^{n-1})\circ {\mathbf{h}}_{\tau }^{n-1}\right]\\ {\mathbf{q}}_{\tau }^n,{\mathbf{k}}_{\tau }^n,{\mathbf{v}}_{\tau }^n={\mathbf{h}}_{\tau }^{n-1}{\mathbf{W}}_q^n{}^{\top },{\tilde{\mathbf{h}}}_{\tau }^{n-1}{\mathbf{W}}_{k,E}^n{}^{\top },{\tilde{\mathbf{h}}}_{\tau }^{n-1}{\mathbf{W}}_v^n{}^{\top }\end{array} \\ \begin{array}{c}{\mathbf{A}}_{\tau ,i,j}^n={\mathbf{q}}_{\tau ,i}^n{}^{\top }{\mathbf{k}}_{\tau ,j}^n+{\mathbf{q}}_{\tau ,i}^n{}^{\top }{\mathbf{W}}_{k,R}^n{\mathbf{R}}_{i-j}\\ +u^{\top }{\mathbf{k}}_{\tau ,j}+v^{\top }{\mathbf{W}}_{k,R}^n{\mathbf{R}}_{i-j}\end{array} \\ \begin{array}{l}{\mathbf{a}}_{\tau }^n=\mathbf{Masket}-\mathbf{Softmax}({\mathbf{A}}_{\tau }^n){\mathbf{v}}_{\tau }^n\\ {\mathbf{o}}_{\tau }^n=\mathbf{layerNorm}(\mathbf{Linear}({\mathbf{a}}_{\tau }^n)+{\mathbf{h}}_{\tau }^{n-1})\\ {\mathbf{h}}_{\tau }^n=\mathbf{Positionwise}-\mathbf{Feed}-\mathbf{Forward}({\mathbf{a}}_{\tau }^n)\end{array} \end{gathered}$$

Experiments

Conclusions

Transformer-XL获得了强大的困惑度结果，比RNN和Transformer建立了更长期的依赖关系，在评估过程中实现了大幅提速，并且能够生成连贯的文本文章。我们设想Transformer-XL在文本生成、无监督的特征学习、图像和语音建模等领域的有趣应用

Remark

话好多。。