P1144 最短路计数最短路，bfs(回顾

原创于 2022-03-16 22:55:12 发布 · 226 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#宽度优先 #图论 #算法

洛谷专栏收录该内容

44 篇文章

订阅专栏

本文介绍了如何利用Dijkstra算法计算从节点1到其他节点的最短路径，并通过一个AC代码实例展示了当节点1到x1和x2的距离相等时，如何快速求得1到y的最短路数目。代码中，通过队列实现广度优先搜索，动态维护最短路径和最短路数目。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

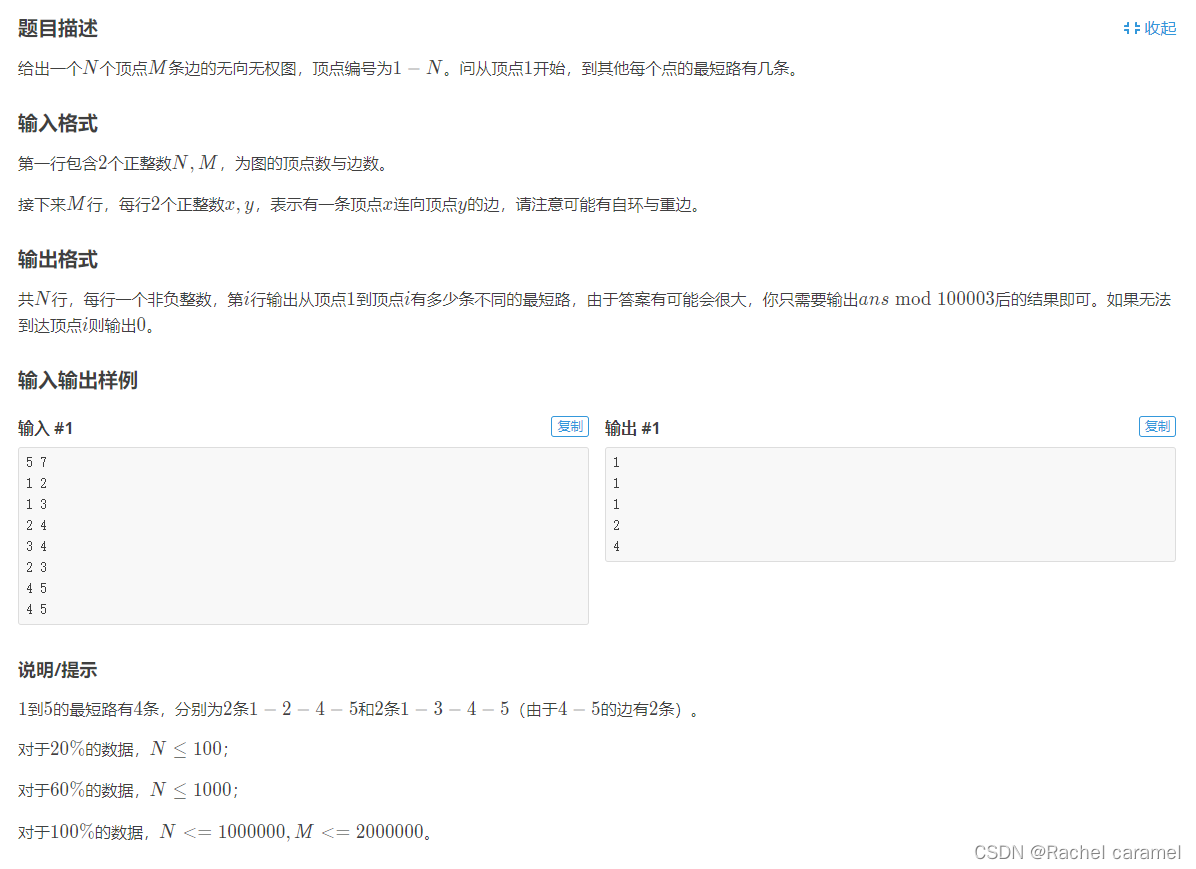
题目：
在这里插入图片描述
思路：
如果从1开始到x1,和x2的距离（x1,和x2和y相连）相同。那么1->y的最短路的数目=1->x1的最短路数目+1->x2的最短路数目
代码说明：
dis[i]表示1-i的最短路的距离；
AC代码：

#include<cstdio>
#include <iostream>
#include<cstring>
#include<algorithm>
#include <vector>
#include <cmath>
#include <queue>
using namespace std;
const int maxn=1000011;
const int mod=100003;
vector <int> e[2*maxn];
queue<int> q;
int n,m,dis[maxn],ans[maxn];
bool vis[maxn];
int main()
{
	scanf("%d%d", &n, &m);
    for(int i=1;i<=m;i++)
    {
        int u,v;
        scanf("%d%d", &u, &v);
        e[u].push_back(v);
        e[v].push_back(u);
    }
    vis[1]=1;
    ans[1]=1;
    q.push(1);
    while(!q.empty())
    {
        int temp1=q.front();
        q.pop();
        for(int i=0;i<e[temp1].size();i++)
        {
            int temp2=e[temp1][i];
            if(!vis[temp2])
            {
                dis[temp2]=dis[temp1]+1;
                vis[temp2]=1;
                q.push(temp2);
            }
            if(dis[temp2]==dis[temp1]+1)
            {
                ans[temp2]=(ans[temp2]+ans[temp1])%mod;
                //cout<<"temp2="<<temp2<<" "<<"ans[temp2]= "<<ans[temp2]<<endl;
            }
        }
    }
    for(int i=1;i<=n;i++) printf("%d\n", ans[i]);
	return 0;
}