CS:APP/深入理解计算机系统-第二章（2.4）

最新推荐文章于 2025-12-26 11:06:25 发布

原创最新推荐文章于 2025-12-26 11:06:25 发布 · 174 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#操作系统 #1024程序员节

CS:APP/深入理解计算机系统学习旅程专栏收录该内容

11 篇文章

订阅专栏

本文介绍了浮点数的二进制表示方法，包括二进制小数和IEEE浮点标准。阐述了浮点数的舍入规则及其在加法、乘法运算中的行为。此外，还讨论了C语言中浮点数的使用和特性。

本节主要介绍浮点数。

2.4.1 二进制小数

首先看看十进制小数的数学表示形式：

这里每个d都是一个0~9的十进制数，i是正还是负取决于d在小数点左边还是右边。

那么尝试使用这种数学表示形式来使用二进制表示小数：

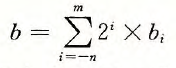
b代表0或1的二进制数，i是正还是负取决于b在小数点左边还是右边。

$101.11_2$ 表示为 $1\times 2^2+0\times2^1+1\times2^0+1\times2^{-1}+1\times2^{-2}=5\frac{3}{4}$

假设我们仅考虑有限长度的编码，那么十进制表示法不能准确表达例如 $\frac{1}{3}$ 这种数。类似，小数的二进制表示法只能表示那些能够被携程 $x\times2^y$ 的数。其他的值只能够被近似地表示。例如，数字 $\frac{1}{5}$ 可以用十进制小数0.20精确表示。不过，我们不能把它准确地表示为一个二进制小数，我们只能近似地表示，通过增加二进制表示的长度可以提高表示的精度。

2.4.2 IEEE浮点表示

前面使用的表示法不能很有效地表示非常大的数字。例如，表达式 $5\times 2^{100}$ 是用101后面跟随100个零的位模式来表示。相反，我们希望的是通过给定x和y的值，来表示形如 $x\times2^y$ 的数。

IEEE浮点标准用 $V=(-1)^s\times M\times 2^E$ 的形式来表示一个数：

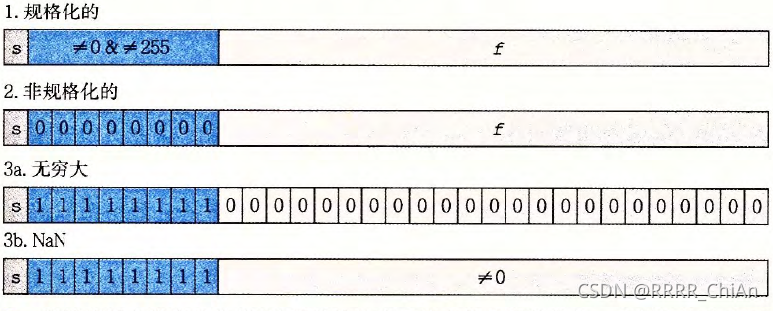
符号(sign) s决定当前数是负数还是整数，对于数值0的符号位解释作为特殊情况处理。

尾数(significand) M是一个二进制小数，它的范围是1~2- $\varepsilon$ ，或者是0~1- $\varepsilon$ 。

阶码(exponent) E的作用是对浮点数加权，这个权重是2的E次幂（可能是负数）。

将浮点数的位表示划分为三个字段，分别对这些值进行编码：

一个单独的符号位s直接编码符号s
k位的阶段字码 $exp=e_{k-1}...e_1e_0$ 编码阶码E
n位小数字段 $frac=f_{n-1}...f_1f_0$ 编码尾数M，但是编码出来的值也依赖于阶码字段的值是否等于0

在单精度浮点格式float中，s、exp和frac分别是1bit、8bit和23bit，得到一个32bit的表示；在双精度浮点格式double中，s、exp和frac分别是1bit、11bit和52bit，得到一个64bit的表示。

给定位表示，根据exp的值，被编码的值可以分成几种不同的情况，下图以float为例进行说明：

2.4.3 数字示例

假设现在有1bit符号、4bit阶码和3bit小数，他们所能表示的值如下表格所示：（此时偏置量bias为 $2^{4-1}-1=7$ ，假设符号位为0，仅考虑正数）

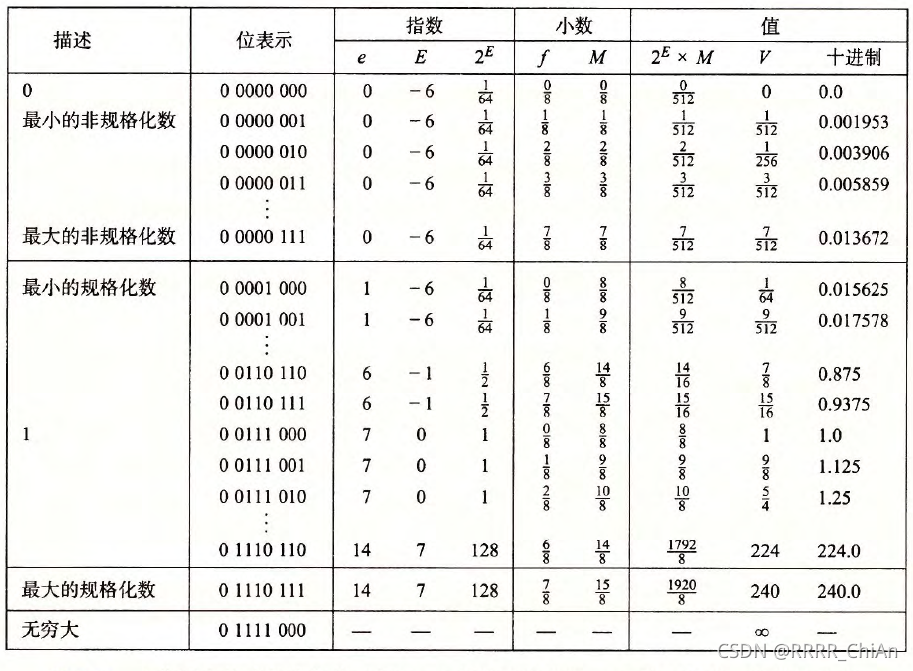
下表同时展示了单精度和双精度浮点数的表示和数字值

下面是k位阶码和n位小数的浮点表示的一般属性

2.4.4 舍入

IEEE浮点格式定义了四种不同的舍入方式。默认的方法是找到最接近的匹配，而其他三种可用于计算上界和下界。如下表所示（注意下表中的1.5和2.5的向偶数舍入结果，理解“向偶数”的含义）：

向偶数舍入有什么好处？

假想到这样的情景：这种方法舍入一组数值，会在计算这些值的平均数中引入统计偏差。我们采用这种方式舍入得到的一组数的平均值将比这些数本身的平均值略高一些。相反，如果我们总是把两个可表示值中间的数字向下舍入，那么舍入后的一组数的平均值将比这些数本身的平均值略低一些。向偶数舍入在大多数现实情况中避免了这种统计偏差。在50% 的时间里，它将向上舍入，而在50% 的时间里，它将向下舍入。

在我们不想舍入到整数时，也可以使用向偶数舍入。我们只是简单地考虑最低有效数字是奇数还是偶数。例如，假设我们想将十进制数舍入到最接近的百分位。不管用那种舍入方式，我们都将把1. 2349999舍入到1. 23, 而将1. 2350001舍入到1. 24, 因为它们不是在1. 23和1. 24的正中间。另一方面我们将把两个数1. 2350000 和1. 2450000 都舍入到1. 24, 因为4是偶数。

相似地，向偶数舍入法能够运用在二进制小数上。我们将最低有效位的值0 认为是偶数，值1 认为是奇数。一般来说，只有对形如XX...X.YY...Y的二进制位模式的数，这种舍入方式才有效，其中X 和Y 表示任意位值，最右边的Y 是要被舍人的位置。只有这种位模式表示在两个可能的结果正中间的值。

2.4.5 浮点运算

IEEE标准制定了一个规则来确定诸如加法和乘法这样的算术运算的结果。把浮点值x和y看成实数，而某个运算 $\odot$ 定义在实数上，计算将产生Round(x $\odot$ y)，这是对实际运算的精确结果进行舍入后的结果。在实际中，浮点单元的设计者使用一些聪明的小技巧来避免执行这种精确的计算，因为计算只要精确到能够保证得到一个正确的舍入结果就可以了。当参数中有一个是特殊值（例如-0，-无穷或者NaN）时，IEEE标准定义了一些使之更加合理的规则。例如，定义1/-0为-∞，1/+0为+∞。