CS:APP/深入理解计算机系统-第二章（2.2）

2.2.1 整型数据类型

以C语言为例，32和64位程序的不同类型的整型数据取值范围如下所示：

（32bit）

 （64bit）

 2.2.2 无符号数的编码

无符号数的表示有一个很重要的属性：介于0~-1之间的数有一个唯一的w位的值编码。例如，有一个无符号的十进制数11，有一个4位的二进制表示，即1011。

 2.2.3 补码编码

计算机中使用补码表示负数。

对于补码来说，二进制表示中的最高有效位叫做符号位，0表示正数，1表示负数，例如，0001表示1，0101表示5，1011表示-5，1111表示-1。

w位补码所能表示的最小值就是[10...0]，整数值表示-，最大值是[01...0]，整数值表示。补码表示也具有唯一性。

C 语言标准并没有要求要用补码形式来表示有符号整数，但是几乎所有的机器都是这么做的。

 2.2.4 有符号数和无符号数之间的转换

对于大多数C 语言的实现，处理同样字长的有符号数和无符号数之间相互转换的一般规则是：数值可能会改变，但是位模式不变。

从补码转换成无符号数的数学公式为： 

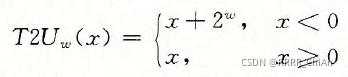
从无符号数转换成补码的数学公式为：

 

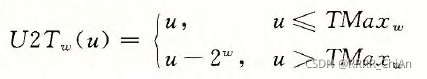
其中0≤u≤ 

 2.2.5 C语言中的有符号数与无符号数

由于C 语言对同时包含有符号和无符号数表达式的这种处理方式，出现了一些奇特的行为。当执行一个运算时，如果它的一个运算数是有符号的而另一个是无符号的，那么C语言会隐式地将有符号参数强制类型转换为无符号数，并假设这两个数都是非负的，来执 行这个运算。就像我们将要看到的，这种方法对于标准的算术运算来说并无多大差异，但 是对于像＜和＞这样的关系运算符来说，它会导致非直观的结果。下展示了一些关系表达式的示例以及它们得到的求值结果，这里假设数据类型int 表示为32 位补码。考虑比较式-1<0U 。因为第二个运算数是无符号的，第一个运算数就会被隐式地转换为无符号数，因此表达式就等价于4294967295U<0U(), 这个答案显然是错的。其他那些示例也可以通过相似的分析来理解。

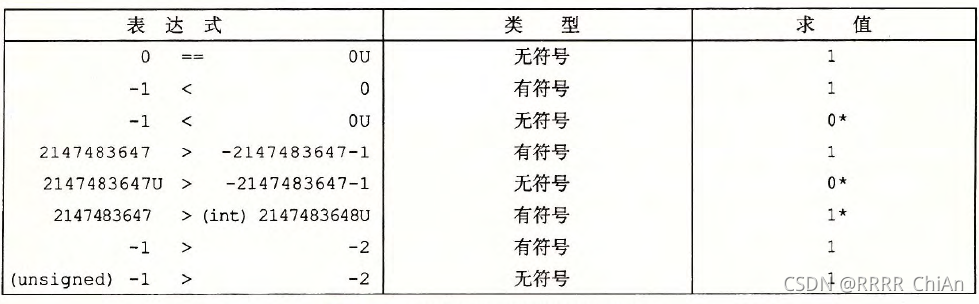
2.2.6 扩展一个数字的位表示

 一个常见的运算是在不同字长的整数之间转换，同时又保持数值不变。当然，当目标数据类型太小以至于不能表示想要的值时，这根本就是不可能的。然而，从一个较小的数据类型转换到一个较大的类型，应该总是可能的。

 有两种扩展表示，分别为用于无符号数的零扩展和用于补码数的符号扩展。

 顾名思义，零扩展就是前面加0，符号扩展就是前面加代表符号的0/1。

2.2.7 截断数字

对于无符号数，截断后的结果 = 截断前的结果 mod ，其中k表示截断k位

对于有符号数，阶段后的结果 = ，其中k表示截断k位

2.2.8 关于有符号数与无符号数的建议

有符号数到无符号数的隐式强制类型转换导致了某些非直观的行为。而这些非直观的特性经常导致程序错误，并且这种包含隐式强制类型转换的细微差别的错误很难被发现。因为这种强制类型转换是在代码中没有明确指示的情况下发生的，程序员经常忽视了它的影响。

简单来说，不要闲得无聊在有符号和无符号里面来回横跳。